Giải Toán 9 bài 3: Giải hệ phương trình bằng phương pháp thế
Giải bài tập Toán lớp 9 bài 3: Giải hệ phương trình bằng phương pháp thế
Giải bài tập SGK Toán lớp 9 bài 3: Giải hệ phương trình bằng phương pháp thế tổng hợp đáp án chi tiết cho các bài tập trong sgk Toán 9 giúp các em nắm vững kiến thức được học và luyện giải Toán 9 hiệu quả.
Trả lời câu hỏi Toán 9 Bài 3
Câu hỏi 1
Giải hệ phương trình sau bằng phương pháp thế (biểu diễn y theo x từ phương trình thứ hai của hệ)
![]() \(\left\{ \begin{matrix}
4x-5y=3 \\
3x-y=16 \\
\end{matrix} \right.\)
\(\left\{ \begin{matrix}
4x-5y=3 \\
3x-y=16 \\
\end{matrix} \right.\)
Hướng dẫn giải
Ta biểu diễn y theo x từ phương trình thứ hai ta có:
![]() \(\left\{ \begin{matrix}
4x-5y=3 \\
3x-y=16 \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
4x-5y=3 \\
y=3x-16 \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
4x-5.\left( 3x-16 \right)=3 \\
y=3x-16 \\
\end{matrix} \right.\)
\(\left\{ \begin{matrix}
4x-5y=3 \\
3x-y=16 \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
4x-5y=3 \\
y=3x-16 \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
4x-5.\left( 3x-16 \right)=3 \\
y=3x-16 \\
\end{matrix} \right.\)
![]() \(\Leftrightarrow \left\{ \begin{matrix}
-11x+80=3 \\
y=3x-16 \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
x=7 \\
y=5 \\
\end{matrix} \right.\)
\(\Leftrightarrow \left\{ \begin{matrix}
-11x+80=3 \\
y=3x-16 \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
x=7 \\
y=5 \\
\end{matrix} \right.\)
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (7; 5)
Câu hỏi 2
Bằng minh họa hình học và bằng phương pháp thế, chứng tỏ rằng hệ (IV) vô số nghiệm.
![]() \(\left( III \right)\left\{ \begin{matrix}
4x-2y=-6 \\
-2x+y=3 \\
\end{matrix} \right.\)
\(\left( III \right)\left\{ \begin{matrix}
4x-2y=-6 \\
-2x+y=3 \\
\end{matrix} \right.\)
Hướng dẫn giải
Minh họa hình học
 \(\left( III \right)\left\{ \begin{matrix}
4x-2y=-6 \\
-2x+y=3 \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
2y=4x+6\text{ (d)} \\
y=2x+3\text{ (d }\!\!'\!\!\text{ )} \\
\end{matrix} \right.\)
\(\left( III \right)\left\{ \begin{matrix}
4x-2y=-6 \\
-2x+y=3 \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
2y=4x+6\text{ (d)} \\
y=2x+3\text{ (d }\!\!'\!\!\text{ )} \\
\end{matrix} \right.\)
Biểu diễn hai đường thẳng d và d’ như hình vẽ sau:
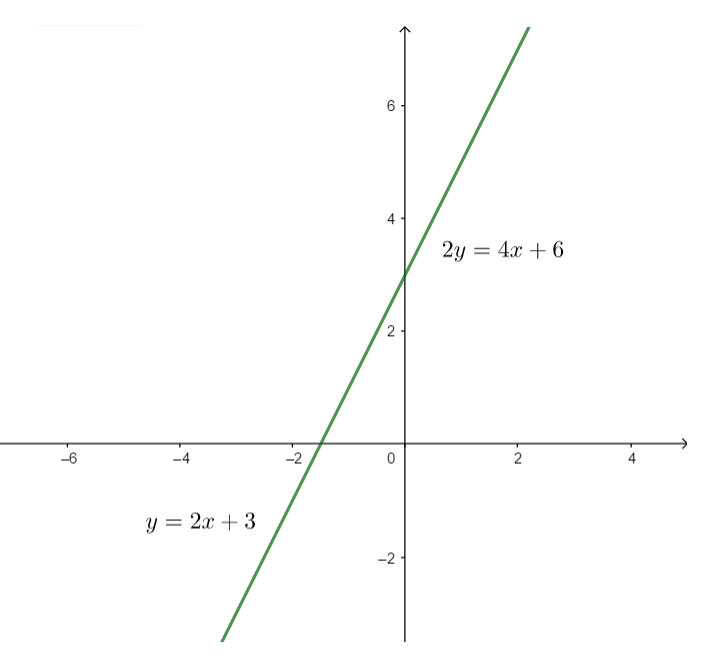
Nhận xét: Hai đường thẳng trên trùng nhau hay hệ phương trình (III) vô số nghiệm.
Giải Toán 9 trang 15 tập 2
Bài 12 (trang 15 SGK Toán 9 Tập 2)
Giải các hệ phương trình sau bằng phương pháp thế:
a) ![]() \(\left\{\begin{matrix} x - y =3 & & \\ 3x-4y=2 & & \end{matrix}\right.\)
\(\left\{\begin{matrix} x - y =3 & & \\ 3x-4y=2 & & \end{matrix}\right.\)
b) ![]() \(\left\{\begin{matrix} 7x - 3y =5 & & \\ 4x+y=2 & & \end{matrix}\right.\)
\(\left\{\begin{matrix} 7x - 3y =5 & & \\ 4x+y=2 & & \end{matrix}\right.\)
c) ![]() \(\left\{\begin{matrix} x +3y =-2 & & \\ 5x-4y=11 & & \end{matrix}\right.\)
\(\left\{\begin{matrix} x +3y =-2 & & \\ 5x-4y=11 & & \end{matrix}\right.\)
a) ![]() \(\left\{\begin{matrix} x - y =3 & & \\ 3x-4y=2 & & \end{matrix}\right.\)
\(\left\{\begin{matrix} x - y =3 & & \\ 3x-4y=2 & & \end{matrix}\right.\)
Rút x từ phương trình trên rồi thế vào phương trình dưới , ta được:
![]() \(\left\{ \matrix{
x - y = 3 \hfill \cr
3x - 4y = 2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 3 + y \hfill \cr
3\left( {3 + y} \right) - 4y = 2 \hfill \cr} \right.\)
\(\left\{ \matrix{
x - y = 3 \hfill \cr
3x - 4y = 2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 3 + y \hfill \cr
3\left( {3 + y} \right) - 4y = 2 \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
x = 3 + y \hfill \cr
9 + 3y - 4y = 2 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = 3 + y \hfill \cr
9 + 3y - 4y = 2 \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
x = 3 + y \hfill \cr
- y = 2 - 9 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 3 + y \hfill \cr
y = 7 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 3 + 7 \hfill \cr
y = 7 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = 3 + y \hfill \cr
- y = 2 - 9 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 3 + y \hfill \cr
y = 7 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 3 + 7 \hfill \cr
y = 7 \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
x = 10 \hfill \cr
y = 7 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = 10 \hfill \cr
y = 7 \hfill \cr} \right.\)
Vậy hệ đã cho có nghiệm là (x;y)=(10; 7).
b) ![]() \(\left\{\begin{matrix} 7x - 3y =5 & & \\ 4x+y=2 & & \end{matrix}\right.\)
\(\left\{\begin{matrix} 7x - 3y =5 & & \\ 4x+y=2 & & \end{matrix}\right.\)
Rút y từ phương trình dưới rồi thế vào phương trình trên, ta có:
![]() \(\left\{ \begin{array}{l}7x - 3y = 5\\4x + y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x - 3y = 5\\y = 2 - 4x\end{array} \right.\)
\(\left\{ \begin{array}{l}7x - 3y = 5\\4x + y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x - 3y = 5\\y = 2 - 4x\end{array} \right.\)
![]() \(\Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\7x - 3.\left( {2 - 4x} \right) = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\7x - 6 + 12x = 5\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\7x - 3.\left( {2 - 4x} \right) = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\7x - 6 + 12x = 5\end{array} \right.\)
![]() \(\Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\7x + 12x = 5 + 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\19x = 11\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\7x + 12x = 5 + 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\19x = 11\end{array} \right.\)
 \(\Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\x = \dfrac{{11}}{{19}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{11}}{{19}}\\y = 2 - 4.\dfrac{{11}}{{19}}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{11}}{{19}}\\y = - \dfrac{6}{{19}}\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\x = \dfrac{{11}}{{19}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{11}}{{19}}\\y = 2 - 4.\dfrac{{11}}{{19}}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{11}}{{19}}\\y = - \dfrac{6}{{19}}\end{array} \right.\)
Vậy hệ có nghiệm duy nhất là ![]() \({\left(\dfrac{11}{19}; \dfrac{-6}{19} \right)}\)
\({\left(\dfrac{11}{19}; \dfrac{-6}{19} \right)}\)
c) ![]() \(\left\{\begin{matrix} x +3y =-2 & & \\ 5x-4y=11 & & \end{matrix}\right.\)
\(\left\{\begin{matrix} x +3y =-2 & & \\ 5x-4y=11 & & \end{matrix}\right.\)
Rút x từ phương trình trên rồi thế vào phương trình dưới, ta có:
![]() \(\left\{ \matrix{
x + 3y = - 2 \hfill \cr
5x - 4y = 11 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 2 - 3y \hfill \cr
5\left( { - 2 - 3y} \right) - 4y = 11 \hfill \cr} \right.\)
\(\left\{ \matrix{
x + 3y = - 2 \hfill \cr
5x - 4y = 11 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 2 - 3y \hfill \cr
5\left( { - 2 - 3y} \right) - 4y = 11 \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
x = - 2 - 3y \hfill \cr
- 10 - 15y - 4y = 11 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = - 2 - 3y \hfill \cr
- 10 - 15y - 4y = 11 \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
x = - 2 - 3y \hfill \cr
- 15y - 4y = 11 + 10 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 2 - 3y \hfill \cr
- 19y = 21 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = - 2 - 3y \hfill \cr
- 15y - 4y = 11 + 10 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 2 - 3y \hfill \cr
- 19y = 21 \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
x = - 2 - 3y \hfill \cr
y = - \dfrac{ 21}{ 19} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = - 2 - 3y \hfill \cr
y = - \dfrac{ 21}{ 19} \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
x = - 2 - 3. \dfrac{ - 21}{19} \hfill \cr
y = - \dfrac{21}{19} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = \dfrac{25}{19} \hfill \cr
y = - \dfrac{21}{19} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = - 2 - 3. \dfrac{ - 21}{19} \hfill \cr
y = - \dfrac{21}{19} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = \dfrac{25}{19} \hfill \cr
y = - \dfrac{21}{19} \hfill \cr} \right.\)
Vậy hệ có nghiệm duy nhất là ![]() \({\left(\dfrac{25}{19}; \dfrac{-21}{19} \right)}\)
\({\left(\dfrac{25}{19}; \dfrac{-21}{19} \right)}\)
Bài 13 (trang 15 SGK Toán 9 Tập 2)
Giải các hệ phương trình sau bằng phương pháp thế:
a) ![]() \(\left\{\begin{matrix} 3x - 2y = 11 & & \\ 4x - 5y = 3& & \end{matrix}\right.;\)
\(\left\{\begin{matrix} 3x - 2y = 11 & & \\ 4x - 5y = 3& & \end{matrix}\right.;\)
b)  \(\left\{\begin{matrix} \dfrac{x}{2}- \dfrac{y}{3} = 1& & \\ 5x - 8y = 3& & \end{matrix}\right.\)
\(\left\{\begin{matrix} \dfrac{x}{2}- \dfrac{y}{3} = 1& & \\ 5x - 8y = 3& & \end{matrix}\right.\)
a) Ta có:
![]() \(\left\{ \matrix{
3x - 2y = 11 \hfill \cr
4x - 5y = 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
2y = 3x - 11 \hfill \cr
4x - 5y = 3 \hfill \cr} \right.\)
\(\left\{ \matrix{
3x - 2y = 11 \hfill \cr
4x - 5y = 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
2y = 3x - 11 \hfill \cr
4x - 5y = 3 \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
y = \dfrac{3x - 11}{2}\ (1) \hfill \cr
4x - 5.\dfrac{3x - 11}{ 2} = 3 \ (2) \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
y = \dfrac{3x - 11}{2}\ (1) \hfill \cr
4x - 5.\dfrac{3x - 11}{ 2} = 3 \ (2) \hfill \cr} \right.\)
Giải phương trình (2):
![]() \(4x - 5.\dfrac{3x - 11}{ 2} = 3
\Leftrightarrow 4x - \dfrac{15x - 55}{ 2} = 3\)
\(4x - 5.\dfrac{3x - 11}{ 2} = 3
\Leftrightarrow 4x - \dfrac{15x - 55}{ 2} = 3\)
![]() \(\Leftrightarrow \dfrac{4x.2}{2} - \dfrac{15x - 55}{ 2} = \dfrac{3.2}{2}
\Leftrightarrow \dfrac{8x}{2} - \dfrac{15x - 55}{2} = \dfrac{6}{2}\)
\(\Leftrightarrow \dfrac{4x.2}{2} - \dfrac{15x - 55}{ 2} = \dfrac{3.2}{2}
\Leftrightarrow \dfrac{8x}{2} - \dfrac{15x - 55}{2} = \dfrac{6}{2}\)
![]() \(\Leftrightarrow \dfrac{8x - 15x + 55}{2} = \dfrac{6}{2}
\Leftrightarrow 8x - 15x + 55 = 6
\Leftrightarrow - 7x = 6 - 55\)
\(\Leftrightarrow \dfrac{8x - 15x + 55}{2} = \dfrac{6}{2}
\Leftrightarrow 8x - 15x + 55 = 6
\Leftrightarrow - 7x = 6 - 55\)
![]() \(\Leftrightarrow - 7x = - 49
\Leftrightarrow x=7\)
\(\Leftrightarrow - 7x = - 49
\Leftrightarrow x=7\)
Thay x=7 vào phương trình (1), ta được:
![]() \(y = \dfrac{3.7 - 11}{2}=5\)
\(y = \dfrac{3.7 - 11}{2}=5\)
Vậy hệ có nghiệm duy nhất là (7; 5).
b) Ta có:
 \(\left\{ \matrix{
\dfrac{x}{2} - \dfrac{y}{3} = 1 \hfill \cr
5x - 8y = 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
\dfrac{x }{2} = 1 + \dfrac{y}{3} \hfill \cr
5x - 8y = 3 \hfill \cr} \right.\)
\(\left\{ \matrix{
\dfrac{x}{2} - \dfrac{y}{3} = 1 \hfill \cr
5x - 8y = 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
\dfrac{x }{2} = 1 + \dfrac{y}{3} \hfill \cr
5x - 8y = 3 \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
x = 2 + \dfrac{2y}{3} \ (1) \hfill \cr
5{\left(2 + \dfrac{2y}{3} \right)} - 8y = 3 \ (2) \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = 2 + \dfrac{2y}{3} \ (1) \hfill \cr
5{\left(2 + \dfrac{2y}{3} \right)} - 8y = 3 \ (2) \hfill \cr} \right.\)
Giải phương trình (2), ta được:
![]() \(5{\left(2 + \dfrac{2y}{3} \right)} - 8y = 3
\Leftrightarrow 5.2 + 5. \dfrac{2y}{3}-8y = 3
\Leftrightarrow 10 + \dfrac{10y}{3} -8y =3\)
\(5{\left(2 + \dfrac{2y}{3} \right)} - 8y = 3
\Leftrightarrow 5.2 + 5. \dfrac{2y}{3}-8y = 3
\Leftrightarrow 10 + \dfrac{10y}{3} -8y =3\)
![]() \(\Leftrightarrow \dfrac{30}{3} +\dfrac{10y}{3} - \dfrac{24y}{3} = \dfrac{9}{3}
\Leftrightarrow 30+ 10y -24y=9\)
\(\Leftrightarrow \dfrac{30}{3} +\dfrac{10y}{3} - \dfrac{24y}{3} = \dfrac{9}{3}
\Leftrightarrow 30+ 10y -24y=9\)
![]() \(\Leftrightarrow -14y=9-30
\Leftrightarrow -14y=-21\)
\(\Leftrightarrow -14y=9-30
\Leftrightarrow -14y=-21\)
![]() \(\Leftrightarrow y=\dfrac{21}{14}
\Leftrightarrow y= \dfrac{3}{2}\)
\(\Leftrightarrow y=\dfrac{21}{14}
\Leftrightarrow y= \dfrac{3}{2}\)
Thay ![]() \(y= \dfrac{3}{2}\)vào (1), ta được:
\(y= \dfrac{3}{2}\)vào (1), ta được:
 \(x = 2 + \dfrac{2. \dfrac{3}{2}}{3}=2+\dfrac{3}{3}=3.\)
\(x = 2 + \dfrac{2. \dfrac{3}{2}}{3}=2+\dfrac{3}{3}=3.\)
Vậy hệ phương trình có nghiệm duy nhất ![]() \({\left(3; \dfrac{3}{2} \right)}.\)
\({\left(3; \dfrac{3}{2} \right)}.\)
Bài 14 (trang 15 SGK Toán 9 Tập 2)
Giải các hệ phương trình bằng phương pháp thế:
a)  \(\left\{\begin{matrix} x + y\sqrt{5} = 0& & \\ x\sqrt{5} + 3y = 1 - \sqrt{5}& & \end{matrix}\right.\)
\(\left\{\begin{matrix} x + y\sqrt{5} = 0& & \\ x\sqrt{5} + 3y = 1 - \sqrt{5}& & \end{matrix}\right.\)
b)  \(\left\{\begin{matrix} (2 - \sqrt{3})x - 3y = 2 + 5\sqrt{3}& & \\ 4x + y = 4 -2\sqrt{3}& & \end{matrix}\right.\)
\(\left\{\begin{matrix} (2 - \sqrt{3})x - 3y = 2 + 5\sqrt{3}& & \\ 4x + y = 4 -2\sqrt{3}& & \end{matrix}\right.\)
a) Ta có:
 \(\left\{ \matrix{
x + y\sqrt 5 = 0 \hfill \cr
x\sqrt 5 + 3y = 1 - \sqrt 5 \hfill \cr} \right.\)
\(\left\{ \matrix{
x + y\sqrt 5 = 0 \hfill \cr
x\sqrt 5 + 3y = 1 - \sqrt 5 \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
x = - y\sqrt 5 \hfill \cr
\left( { - y\sqrt 5 } \right).\sqrt 5 + 3y = 1 - \sqrt 5 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = - y\sqrt 5 \hfill \cr
\left( { - y\sqrt 5 } \right).\sqrt 5 + 3y = 1 - \sqrt 5 \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
x = - y\sqrt 5 \hfill \cr
- 5y + 3y = 1 - \sqrt 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - y\sqrt 5 \hfill \cr
- 2y = 1 - \sqrt 5 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = - y\sqrt 5 \hfill \cr
- 5y + 3y = 1 - \sqrt 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - y\sqrt 5 \hfill \cr
- 2y = 1 - \sqrt 5 \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
x = - y\sqrt 5 \hfill \cr
y = \dfrac{1 - \sqrt 5 }{ - 2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - y\sqrt 5 \hfill \cr
y = \dfrac{\sqrt 5 - 1}{2} \hfill \cr} \right.
\Leftrightarrow \left\{ \matrix{
x = - \dfrac{\sqrt 5 - 1}{ 2}.\sqrt 5 \hfill \cr
y = \dfrac{\sqrt 5 - 1}{2} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = - y\sqrt 5 \hfill \cr
y = \dfrac{1 - \sqrt 5 }{ - 2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - y\sqrt 5 \hfill \cr
y = \dfrac{\sqrt 5 - 1}{2} \hfill \cr} \right.
\Leftrightarrow \left\{ \matrix{
x = - \dfrac{\sqrt 5 - 1}{ 2}.\sqrt 5 \hfill \cr
y = \dfrac{\sqrt 5 - 1}{2} \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
x = - \dfrac{5 - \sqrt 5 }{2} \hfill \cr
y = \dfrac{\sqrt 5 - 1}{2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = \dfrac{\sqrt 5 - 5}{ 2} \hfill \cr
y = \dfrac{\sqrt 5 - 1}{ 2} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = - \dfrac{5 - \sqrt 5 }{2} \hfill \cr
y = \dfrac{\sqrt 5 - 1}{2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = \dfrac{\sqrt 5 - 5}{ 2} \hfill \cr
y = \dfrac{\sqrt 5 - 1}{ 2} \hfill \cr} \right.\)
Vậy hệ phương trình có nghiệm duy nhất  \({\left(\dfrac{\sqrt 5 - 5}{ 2} ; \dfrac{\sqrt 5 - 1}{ 2} \right)}\)
\({\left(\dfrac{\sqrt 5 - 5}{ 2} ; \dfrac{\sqrt 5 - 1}{ 2} \right)}\)
b)  \(\left\{\begin{matrix} (2 - \sqrt{3})x - 3y = 2 + 5\sqrt{3}& & \\ 4x + y = 4 -2\sqrt{3}& & \end{matrix}\right.\)
\(\left\{\begin{matrix} (2 - \sqrt{3})x - 3y = 2 + 5\sqrt{3}& & \\ 4x + y = 4 -2\sqrt{3}& & \end{matrix}\right.\)
Ta có:
 \(\left\{ \matrix{
\left( {2 - \sqrt 3 } \right)x - 3y = 2 + 5\sqrt 3 \hfill \cr
4x + y = 4 - 2\sqrt 3 \hfill \cr} \right.
\Leftrightarrow \left\{ \matrix{
\left( {2 - \sqrt 3 } \right)x - 3\left( {4 - 2\sqrt 3 - 4x} \right) = 2 + 5\sqrt 3 \ (1) \hfill \cr
y = 4 - 2\sqrt 3 - 4x \ (2) \hfill \cr} \right.\)
\(\left\{ \matrix{
\left( {2 - \sqrt 3 } \right)x - 3y = 2 + 5\sqrt 3 \hfill \cr
4x + y = 4 - 2\sqrt 3 \hfill \cr} \right.
\Leftrightarrow \left\{ \matrix{
\left( {2 - \sqrt 3 } \right)x - 3\left( {4 - 2\sqrt 3 - 4x} \right) = 2 + 5\sqrt 3 \ (1) \hfill \cr
y = 4 - 2\sqrt 3 - 4x \ (2) \hfill \cr} \right.\)
Giải phương trình (1), ta được:
![]() \(( 2 - \sqrt 3 )x - 3(4 - 2\sqrt 3 - 4x) = 2 + 5\sqrt 3
\Leftrightarrow 2x -\sqrt 3 x -12 + 6 \sqrt 3 + 12x=2+ 5 \sqrt 3\)
\(( 2 - \sqrt 3 )x - 3(4 - 2\sqrt 3 - 4x) = 2 + 5\sqrt 3
\Leftrightarrow 2x -\sqrt 3 x -12 + 6 \sqrt 3 + 12x=2+ 5 \sqrt 3\)
![]() \(\Leftrightarrow 2x -\sqrt 3 x + 12x=2+ 5 \sqrt 3 +12 -6 \sqrt 3
\Leftrightarrow (2 -\sqrt 3 + 12)x= 2+12 +5\sqrt 3 -6 \sqrt 3\)
\(\Leftrightarrow 2x -\sqrt 3 x + 12x=2+ 5 \sqrt 3 +12 -6 \sqrt 3
\Leftrightarrow (2 -\sqrt 3 + 12)x= 2+12 +5\sqrt 3 -6 \sqrt 3\)
![]() \(\Leftrightarrow (14- \sqrt 3)x=14-\sqrt 3
\Leftrightarrow x=1\)
\(\Leftrightarrow (14- \sqrt 3)x=14-\sqrt 3
\Leftrightarrow x=1\)
Thay x=1, vào (2), ta được:
![]() \(y = 4 - 2\sqrt 3 - 4.1=-2 \sqrt 3.\)
\(y = 4 - 2\sqrt 3 - 4.1=-2 \sqrt 3.\)
Vậy hệ phương trình có nghiệm duy nhất ![]() \((1; -2 \sqrt 3).\)
\((1; -2 \sqrt 3).\)
Giải bài tập toán 9 trang 15 tập 2: Luyện tập
Bài 15 (trang 15 SGK Toán 9 Tập 2)
Giải hệ phương trình ![]() \(\left\{\begin{matrix} x + 3y = 1 & & \\ (a^{2} + 1)x + 6y = 2a & & \end{matrix}\right.\)trong mỗi trường hợp sau:
\(\left\{\begin{matrix} x + 3y = 1 & & \\ (a^{2} + 1)x + 6y = 2a & & \end{matrix}\right.\)trong mỗi trường hợp sau:
a) a = -1
b) a = 0
c) a = 1
a) a = -1
Thay a = -1 vào hệ, ta được:
 \(\left\{\begin{matrix} x + 3y = 1 & & \\ {\left((-1)^2+1 \right)}x+ 6y = 2.(-1) & & \end{matrix}\right.
\Leftrightarrow \left\{\begin{matrix} x + 3y = 1 & & \\ 2x+ 6y = -2 & & \end{matrix}\right.\)
\(\left\{\begin{matrix} x + 3y = 1 & & \\ {\left((-1)^2+1 \right)}x+ 6y = 2.(-1) & & \end{matrix}\right.
\Leftrightarrow \left\{\begin{matrix} x + 3y = 1 & & \\ 2x+ 6y = -2 & & \end{matrix}\right.\)
![]() \(\Leftrightarrow \left\{\begin{matrix} x + 3y = 1 & & \\ x+ 3y = -1 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x = 1 -3y & & \\ (1-3y)+ 3y = -1 & & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x + 3y = 1 & & \\ x+ 3y = -1 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x = 1 -3y & & \\ (1-3y)+ 3y = -1 & & \end{matrix}\right.\)
 \(\Leftrightarrow \left\{\begin{matrix} x = 1 -3y & & \\ 1 = -1 (vô \ lý )& & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x = 1 -3y & & \\ 1 = -1 (vô \ lý )& & \end{matrix}\right.\)
Vậy hệ phương trình trên vô nghiệm.
b) a = 0
Thay a = 0 vào hệ, ta được:
![]() \(\left\{ \matrix{
x + 3y = 1 \hfill \cr
\left( {0 + 1} \right)x + 6y = 2.0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x + 3y = 1 \hfill \cr
x + 6y = 0 \hfill \cr} \right.\)
\(\left\{ \matrix{
x + 3y = 1 \hfill \cr
\left( {0 + 1} \right)x + 6y = 2.0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x + 3y = 1 \hfill \cr
x + 6y = 0 \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
x + 3y = 1 \hfill \cr
x = - 6y \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x + 3y = 1 \hfill \cr
x = - 6y \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
- 6y + 3y = 1 \hfill \cr
x = - 6y \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
- 3y = 1 \hfill \cr
x = - 6y \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
- 6y + 3y = 1 \hfill \cr
x = - 6y \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
- 3y = 1 \hfill \cr
x = - 6y \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
y = \dfrac{ - 1}{3} \hfill \cr
x = - 6y \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = \dfrac{ - 1}{3} \hfill \cr
x = - 6. \dfrac{ - 1}{3} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = \dfrac{ - 1}{3} \hfill \cr
x = 2 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
y = \dfrac{ - 1}{3} \hfill \cr
x = - 6y \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = \dfrac{ - 1}{3} \hfill \cr
x = - 6. \dfrac{ - 1}{3} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = \dfrac{ - 1}{3} \hfill \cr
x = 2 \hfill \cr} \right.\)
Hệ phương trình có nghiệm![]() \({\left(2; -\dfrac{1}{3} \right)} .\)
\({\left(2; -\dfrac{1}{3} \right)} .\)
c) a = 1
Thay a = 1 vào hệ, ta được:
 \(\left\{ \matrix{
x + 3y = 1 \hfill \cr
({1^2} + 1)x + 6y = 2.1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x + 3y = 1 \hfill \cr
2x + 6y = 2 \hfill \cr} \right.\)
\(\left\{ \matrix{
x + 3y = 1 \hfill \cr
({1^2} + 1)x + 6y = 2.1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x + 3y = 1 \hfill \cr
2x + 6y = 2 \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
x + 3y = 1 \hfill \cr
x + 3y = 1 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x + 3y = 1 \hfill \cr
x + 3y = 1 \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \begin{array}{l}x = 1 - 3y\\1 - 3y + 3y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1 - 3y\\1 = 1\left( {luôn\,đúng} \right)\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}x = 1 - 3y\\1 - 3y + 3y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1 - 3y\\1 = 1\left( {luôn\,đúng} \right)\end{array} \right.\)
Vậy hệ phương trình có vô số nghiệm ![]() \(\left\{ \begin{array}{l}x = 1 - 3y\\y \in \mathbb{R}\end{array} \right.\)
\(\left\{ \begin{array}{l}x = 1 - 3y\\y \in \mathbb{R}\end{array} \right.\)
Bài 16 (trang 16 SGK Toán 9 Tập 2)
Giải các hệ phương trình sau bằng phương pháp thế
a) ![]() \(\left\{\begin{matrix} 3x - y = 5 & & \\ 5x + 2y = 23 & & \end{matrix}\right.\)
\(\left\{\begin{matrix} 3x - y = 5 & & \\ 5x + 2y = 23 & & \end{matrix}\right.\)
b) ![]() \(\left\{\begin{matrix} 3x +5y = 1 & & \\ 2x -y =-8 & & \end{matrix}\right.\)
\(\left\{\begin{matrix} 3x +5y = 1 & & \\ 2x -y =-8 & & \end{matrix}\right.\)
 \(c. \left\{\begin{matrix} \dfrac{x}{y} = \dfrac{2}{3}& & \\ x + y - 10 = 0 & & \end{matrix}\right.\)
\(c. \left\{\begin{matrix} \dfrac{x}{y} = \dfrac{2}{3}& & \\ x + y - 10 = 0 & & \end{matrix}\right.\)
a) Ta có:
![]() \(\left\{ \matrix{
3x - y = 5 \hfill \cr
5x + 2y = 23 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = 3x - 5 \hfill \cr
5x + 2\left( {3x - 5} \right) = 23 \hfill \cr} \right.\)
\(\left\{ \matrix{
3x - y = 5 \hfill \cr
5x + 2y = 23 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = 3x - 5 \hfill \cr
5x + 2\left( {3x - 5} \right) = 23 \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
y = 3x - 5 \hfill \cr
5x + 6x - 10 = 23 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
y = 3x - 5 \hfill \cr
5x + 6x - 10 = 23 \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
y = 3x - 5 \hfill \cr
11x = 23 + 10 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = 3x - 5 \hfill \cr
11x = 33 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
y = 3x - 5 \hfill \cr
11x = 23 + 10 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = 3x - 5 \hfill \cr
11x = 33 \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
y = 3x - 5 \hfill \cr
x = 3 \hfill \cr} \right.
\Leftrightarrow \left\{ \matrix{
y = 3.3 - 5 \hfill \cr
x = 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = 4 \hfill \cr
x = 3 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
y = 3x - 5 \hfill \cr
x = 3 \hfill \cr} \right.
\Leftrightarrow \left\{ \matrix{
y = 3.3 - 5 \hfill \cr
x = 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = 4 \hfill \cr
x = 3 \hfill \cr} \right.\)
Vậy hệ có nghiệm duy nhất là (x; y) = (3; 4).
b) Ta có:
![]() \(\left\{ \matrix{
3x + 5y = 1 \hfill \cr
2x - y = - 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
3x + 5y = 1 \hfill \cr
y = 2x + 8 \hfill \cr} \right.
\Leftrightarrow \left\{ \matrix{
3x + 5\left( {2x + 8} \right) = 1 \hfill \cr
y = 2x + 8 \hfill \cr} \right.\)
\(\left\{ \matrix{
3x + 5y = 1 \hfill \cr
2x - y = - 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
3x + 5y = 1 \hfill \cr
y = 2x + 8 \hfill \cr} \right.
\Leftrightarrow \left\{ \matrix{
3x + 5\left( {2x + 8} \right) = 1 \hfill \cr
y = 2x + 8 \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
3x + 10x + 40 = 1 \hfill \cr
y = 2x + 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
13x = 1 - 40 \hfill \cr
y = 2x + 8 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
3x + 10x + 40 = 1 \hfill \cr
y = 2x + 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
13x = 1 - 40 \hfill \cr
y = 2x + 8 \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
13x = - 39 \hfill \cr
y = 2x + 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 3 \hfill \cr
y = 2x + 8 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
13x = - 39 \hfill \cr
y = 2x + 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 3 \hfill \cr
y = 2x + 8 \hfill \cr} \right.\)
![]() \(\Leftrightarrow \left\{ \matrix{
x = - 3 \hfill \cr
y = 2.\left( { - 3} \right) + 8 \hfill \cr} \right.
\Leftrightarrow \left\{ \matrix{
x = - 3 \hfill \cr
y = 2 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = - 3 \hfill \cr
y = 2.\left( { - 3} \right) + 8 \hfill \cr} \right.
\Leftrightarrow \left\{ \matrix{
x = - 3 \hfill \cr
y = 2 \hfill \cr} \right.\)
Vậy hệ có nghiệm (x; y) = (-3; 2).
c) Ta có:
 \(\left\{ \matrix{
\dfrac{x}{y} = \dfrac{2}{3} \hfill \cr
x + y - 10 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = \dfrac{2y}{3} \hfill \cr
\dfrac{2y}{3} + y = 10 \hfill \cr} \right.\)
\(\left\{ \matrix{
\dfrac{x}{y} = \dfrac{2}{3} \hfill \cr
x + y - 10 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = \dfrac{2y}{3} \hfill \cr
\dfrac{2y}{3} + y = 10 \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
x = \dfrac{2y}{3} \hfill \cr
{\left( \dfrac{2}{3} + 1 \right)}y = 10 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = \dfrac{2y}{3} \hfill \cr
{\left( \dfrac{2}{3} + 1 \right)}y = 10 \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
x = \dfrac{2y}{3} \hfill \cr
\dfrac{5}{ 3}y = 10 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = \dfrac{2y}{3} \hfill \cr
y = 6 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = \dfrac{2y}{3} \hfill \cr
\dfrac{5}{ 3}y = 10 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = \dfrac{2y}{3} \hfill \cr
y = 6 \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
x = \dfrac{2.6}{3} \hfill \cr
y = 6 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 4 \hfill \cr
y = 6 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = \dfrac{2.6}{3} \hfill \cr
y = 6 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 4 \hfill \cr
y = 6 \hfill \cr} \right.\)
Vậy nghiệm của hệ là (x; y) = (4; 6).
Bài 17 (trang 16 SGK Toán 9 Tập 2)
 \(a) \left\{\begin{matrix} x\sqrt{2}- y \sqrt{3}=1 & & \\ x + y\sqrt{3} = \sqrt{2}& & \end{matrix}\right.\)
\(a) \left\{\begin{matrix} x\sqrt{2}- y \sqrt{3}=1 & & \\ x + y\sqrt{3} = \sqrt{2}& & \end{matrix}\right.\)
 \(b) \left\{\begin{matrix} x - 2\sqrt{2} y = \sqrt{5}& & \\ x\sqrt{2} + y = 1 - \sqrt{10}& & \end{matrix}\right.\)
\(b) \left\{\begin{matrix} x - 2\sqrt{2} y = \sqrt{5}& & \\ x\sqrt{2} + y = 1 - \sqrt{10}& & \end{matrix}\right.\)
 \(c. \left\{\begin{matrix} (\sqrt{2}- 1)x - y = \sqrt{2}& & \\ x + (\sqrt{2}+ 1)y = 1& & \end{matrix}\right.\)
\(c. \left\{\begin{matrix} (\sqrt{2}- 1)x - y = \sqrt{2}& & \\ x + (\sqrt{2}+ 1)y = 1& & \end{matrix}\right.\)
a) Ta có:
 \(\left\{ \matrix{
x\sqrt 2 - y\sqrt 3 = 1 \hfill \cr
x + y\sqrt 3 = \sqrt 2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x\sqrt 2 - y\sqrt 3 = 1 \hfill \cr
x = \sqrt 2 - y\sqrt 3 \hfill \cr} \right.\)
\(\left\{ \matrix{
x\sqrt 2 - y\sqrt 3 = 1 \hfill \cr
x + y\sqrt 3 = \sqrt 2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x\sqrt 2 - y\sqrt 3 = 1 \hfill \cr
x = \sqrt 2 - y\sqrt 3 \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
\left( {\sqrt 2-y\sqrt 3 } \right)\sqrt 2 - y\sqrt 3 = 1 \ (1) \hfill \cr
x = \sqrt 2 - y\sqrt 3 \ (2) \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
\left( {\sqrt 2-y\sqrt 3 } \right)\sqrt 2 - y\sqrt 3 = 1 \ (1) \hfill \cr
x = \sqrt 2 - y\sqrt 3 \ (2) \hfill \cr} \right.\)
Giải phương trình (1), ta được:
![]() \(( \sqrt 2 - y\sqrt 3)\sqrt 2 - y\sqrt 3 = 1
\Leftrightarrow (\sqrt 2)^2 - y\sqrt 3 . \sqrt 2 - y\sqrt 3 = 1\)
\(( \sqrt 2 - y\sqrt 3)\sqrt 2 - y\sqrt 3 = 1
\Leftrightarrow (\sqrt 2)^2 - y\sqrt 3 . \sqrt 2 - y\sqrt 3 = 1\)
![]() \(\Leftrightarrow 2 - y\sqrt 3 . \sqrt 2 - y\sqrt 3 = 1
\Leftrightarrow -y\sqrt 3. \sqrt 2 - y\sqrt 3 = 1 - 2\)
\(\Leftrightarrow 2 - y\sqrt 3 . \sqrt 2 - y\sqrt 3 = 1
\Leftrightarrow -y\sqrt 3. \sqrt 2 - y\sqrt 3 = 1 - 2\)
 \(\begin{array}{l}
\Leftrightarrow - y\sqrt 6 - y\sqrt 3 = - 1\\
\Leftrightarrow y\left( {\sqrt 6 + \sqrt 3 } \right) = 1\\
\Leftrightarrow y = \dfrac{1}{{\sqrt 6 + \sqrt 3 }}\\
\Leftrightarrow y = \dfrac{{\sqrt 6 - \sqrt 3 }}{3}\\
\Leftrightarrow y = \dfrac{{\sqrt 3 \left( {\sqrt 2 - 1} \right)}}{3}
\end{array}\)
\(\begin{array}{l}
\Leftrightarrow - y\sqrt 6 - y\sqrt 3 = - 1\\
\Leftrightarrow y\left( {\sqrt 6 + \sqrt 3 } \right) = 1\\
\Leftrightarrow y = \dfrac{1}{{\sqrt 6 + \sqrt 3 }}\\
\Leftrightarrow y = \dfrac{{\sqrt 6 - \sqrt 3 }}{3}\\
\Leftrightarrow y = \dfrac{{\sqrt 3 \left( {\sqrt 2 - 1} \right)}}{3}
\end{array}\)
Thay y tìm được vào phương trình (2), ta được:
![]() \(x = \sqrt 2 - \dfrac{\sqrt 3 (\sqrt 2 -1)}{3}.\sqrt 3\)
\(x = \sqrt 2 - \dfrac{\sqrt 3 (\sqrt 2 -1)}{3}.\sqrt 3\)
![]() \(\Leftrightarrow x=\sqrt 2 - \dfrac{\sqrt 3 .\sqrt 3(\sqrt 2 -1)}{3}
\Leftrightarrow x=\sqrt 2 - \dfrac{ 3(\sqrt 2 -1)}{3} =\sqrt 2 - (\sqrt 2 -1)\)
\(\Leftrightarrow x=\sqrt 2 - \dfrac{\sqrt 3 .\sqrt 3(\sqrt 2 -1)}{3}
\Leftrightarrow x=\sqrt 2 - \dfrac{ 3(\sqrt 2 -1)}{3} =\sqrt 2 - (\sqrt 2 -1)\)
![]() \(\Leftrightarrow x=\sqrt 2 -\sqrt 2 +1=1\\\)
\(\Leftrightarrow x=\sqrt 2 -\sqrt 2 +1=1\\\)
Vậy hệ phương trình đã cho có nghiệm duy nhất là: \({\left( 1;\dfrac{\sqrt 3 (\sqrt 2 -1)}{3} \right)}\)
\({\left( 1;\dfrac{\sqrt 3 (\sqrt 2 -1)}{3} \right)}\)
b) Ta có:
 \(\left\{ \matrix{
x - 2\sqrt 2 y = \sqrt 5 \hfill \cr
x\sqrt 2 + y = 1 - \sqrt {10} \hfill \cr} \right.\)
\(\left\{ \matrix{
x - 2\sqrt 2 y = \sqrt 5 \hfill \cr
x\sqrt 2 + y = 1 - \sqrt {10} \hfill \cr} \right.\)
 \(\Leftrightarrow \left\{ \matrix{
x = 2\sqrt 2 y + \sqrt 5 \ (1) \hfill \cr
\left( {2\sqrt 2 y + \sqrt 5 } \right).\sqrt 2 + y = 1 - \sqrt {10}\ (2) \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = 2\sqrt 2 y + \sqrt 5 \ (1) \hfill \cr
\left( {2\sqrt 2 y + \sqrt 5 } \right).\sqrt 2 + y = 1 - \sqrt {10}\ (2) \hfill \cr} \right.\)
Giải phương trình (2), ta được:
![]() \(\left( {2\sqrt 2 y + \sqrt 5 } \right).\sqrt 2 + y = 1 - \sqrt {10}
\Leftrightarrow 2(\sqrt 2 .\sqrt 2)y + \sqrt 5 .\sqrt 2 + y = 1 - \sqrt {10}\)
\(\left( {2\sqrt 2 y + \sqrt 5 } \right).\sqrt 2 + y = 1 - \sqrt {10}
\Leftrightarrow 2(\sqrt 2 .\sqrt 2)y + \sqrt 5 .\sqrt 2 + y = 1 - \sqrt {10}\)
![]() \(\Leftrightarrow 4y + \sqrt{10}+y=1- \sqrt{10}
\Leftrightarrow 4y +y=1- \sqrt{10}- \sqrt{10}\)
\(\Leftrightarrow 4y + \sqrt{10}+y=1- \sqrt{10}
\Leftrightarrow 4y +y=1- \sqrt{10}- \sqrt{10}\)
![]() \(\Leftrightarrow 5y=1-2 \sqrt{10}
\Leftrightarrow y=\dfrac{1-2 \sqrt{10}}{5}\)
\(\Leftrightarrow 5y=1-2 \sqrt{10}
\Leftrightarrow y=\dfrac{1-2 \sqrt{10}}{5}\)
Thay ![]() \(y=\dfrac{1-2 \sqrt{10}}{5}\) vào (1), ta được:
\(y=\dfrac{1-2 \sqrt{10}}{5}\) vào (1), ta được:
![]() \(x = 2\sqrt 2 .\dfrac{1-2 \sqrt{10}}{5} + \sqrt 5= \dfrac{2\sqrt 2 -4 \sqrt{20}}{5} + \sqrt 5\)
\(x = 2\sqrt 2 .\dfrac{1-2 \sqrt{10}}{5} + \sqrt 5= \dfrac{2\sqrt 2 -4 \sqrt{20}}{5} + \sqrt 5\)
![]() \(\Leftrightarrow x=\dfrac{2\sqrt 2 -4 .2\sqrt{5}}{5} + \sqrt 5=\dfrac{2\sqrt 2 -8\sqrt{5}+ 5\sqrt 5}{5}\)
\(\Leftrightarrow x=\dfrac{2\sqrt 2 -4 .2\sqrt{5}}{5} + \sqrt 5=\dfrac{2\sqrt 2 -8\sqrt{5}+ 5\sqrt 5}{5}\)
![]() \(\Leftrightarrow x=\dfrac{2 \sqrt 2 -3 \sqrt 5}{5}\)
\(\Leftrightarrow x=\dfrac{2 \sqrt 2 -3 \sqrt 5}{5}\)
Vậy hệ có nghiệm duy nhất là:  \((x; y) = {\left(\dfrac{2\sqrt{2} - 3\sqrt{5}}{5};\dfrac{1 - 2\sqrt{10}}{5}\right)}\)
\((x; y) = {\left(\dfrac{2\sqrt{2} - 3\sqrt{5}}{5};\dfrac{1 - 2\sqrt{10}}{5}\right)}\)
c) Ta có:
 \(\left\{ \matrix{
\left( {\sqrt 2 - 1} \right)x - y = \sqrt 2 \hfill \cr
x + \left( {\sqrt 2 + 1} \right)y = 1 \hfill \cr} \right.\)
\(\left\{ \matrix{
\left( {\sqrt 2 - 1} \right)x - y = \sqrt 2 \hfill \cr
x + \left( {\sqrt 2 + 1} \right)y = 1 \hfill \cr} \right.\)
![\left\{ \begin{array}{l}y = \left( {\sqrt 2 - 1} \right)x - \sqrt 2 \,\,\,\,\,\left( 1 \right)\\x + \left( {\sqrt 2 + 1} \right)\left[ {\left( {\sqrt 2 - 1} \right)x - \sqrt 2 } \right] = 1\,\,\,\left( 2 \right)\end{array} \right.](https://st.vndoc.com/data/image/blank.png) \(\left\{ \begin{array}{l}y = \left( {\sqrt 2 - 1} \right)x - \sqrt 2 \,\,\,\,\,\left( 1 \right)\\x + \left( {\sqrt 2 + 1} \right)\left[ {\left( {\sqrt 2 - 1} \right)x - \sqrt 2 } \right] = 1\,\,\,\left( 2 \right)\end{array} \right.\)
\(\left\{ \begin{array}{l}y = \left( {\sqrt 2 - 1} \right)x - \sqrt 2 \,\,\,\,\,\left( 1 \right)\\x + \left( {\sqrt 2 + 1} \right)\left[ {\left( {\sqrt 2 - 1} \right)x - \sqrt 2 } \right] = 1\,\,\,\left( 2 \right)\end{array} \right.\)
Giải phương trình (2), ta được:
![]() \(x + \left( {\sqrt 2 + 1} \right)\left[ { \left( {\sqrt 2 - 1} \right)x} -\sqrt 2 \right] = 1\)
\(x + \left( {\sqrt 2 + 1} \right)\left[ { \left( {\sqrt 2 - 1} \right)x} -\sqrt 2 \right] = 1\)
![]() \(\Leftrightarrow x + (\sqrt 2 + 1) (\sqrt 2 - 1)x -( \sqrt 2 + 1). \sqrt 2 = 1\)
\(\Leftrightarrow x + (\sqrt 2 + 1) (\sqrt 2 - 1)x -( \sqrt 2 + 1). \sqrt 2 = 1\)
![]() \(\Leftrightarrow x + {\left((\sqrt 2)^2 - 1^2 \right)}x-( 2 + \sqrt 2) = 1\)
\(\Leftrightarrow x + {\left((\sqrt 2)^2 - 1^2 \right)}x-( 2 + \sqrt 2) = 1\)
![]() \(\Leftrightarrow x + x = 1+( 2 + \sqrt 2)
\Leftrightarrow 2x =3 +\sqrt 2
\Leftrightarrow x=\dfrac{3+ \sqrt 2}{2}\)
\(\Leftrightarrow x + x = 1+( 2 + \sqrt 2)
\Leftrightarrow 2x =3 +\sqrt 2
\Leftrightarrow x=\dfrac{3+ \sqrt 2}{2}\)
Thay ![]() \(x=\dfrac{3+ \sqrt 2}{2}\)vào (1), ta được:
\(x=\dfrac{3+ \sqrt 2}{2}\)vào (1), ta được:
![]() \(y = \left( {\sqrt 2 - 1} \right).\dfrac{3+ \sqrt 2}{2} - \sqrt 2\)
\(y = \left( {\sqrt 2 - 1} \right).\dfrac{3+ \sqrt 2}{2} - \sqrt 2\)
![]() \(\Leftrightarrow y= \dfrac{(\sqrt 2 - 1 )(3+ \sqrt 2)}{2} - \sqrt 2
\Leftrightarrow y= \dfrac{3\sqrt 2 -3 +2 -\sqrt 2}{2} - \sqrt 2\)
\(\Leftrightarrow y= \dfrac{(\sqrt 2 - 1 )(3+ \sqrt 2)}{2} - \sqrt 2
\Leftrightarrow y= \dfrac{3\sqrt 2 -3 +2 -\sqrt 2}{2} - \sqrt 2\)
![]() \(\Leftrightarrow y= \dfrac{2\sqrt 2 -1}{2} - \sqrt 2
\Leftrightarrow y= \dfrac{2\sqrt 2 -1-2\sqrt 2}{2}
\Leftrightarrow y= \dfrac{-1}{2}\)
\(\Leftrightarrow y= \dfrac{2\sqrt 2 -1}{2} - \sqrt 2
\Leftrightarrow y= \dfrac{2\sqrt 2 -1-2\sqrt 2}{2}
\Leftrightarrow y= \dfrac{-1}{2}\)
Vậy hệ có nghiệm  \((x; y) = {\left(\dfrac{3 + \sqrt{2}}{2};\dfrac{-1}{2} \right)}\)
\((x; y) = {\left(\dfrac{3 + \sqrt{2}}{2};\dfrac{-1}{2} \right)}\)
Bài 18 (trang 16 SGK Toán 9 Tập 2)
a) Xác định các hệ số a và b, biết rằng hệ phương trình
![]() \(\left\{\begin{matrix} 2x + by=-4 & & \\ bx - ay=-5& & \end{matrix}\right.\)
\(\left\{\begin{matrix} 2x + by=-4 & & \\ bx - ay=-5& & \end{matrix}\right.\)
có nghiệm là (1; -2)
b) Cũng hỏi như vậy, nếu hệ phương trình có nghiệm là ![]() \((\sqrt{2} - 1; \sqrt{2}).\)
\((\sqrt{2} - 1; \sqrt{2}).\)
a) Hệ phương trình có nghiệm là (1; -2) khi và chỉ khi (1; -2) thỏa mãn hệ phương trình. Thay x=1, y=-2 vào hệ, ta có:
![]() \(\left\{\begin{matrix} 2 - 2b=-4 & & \\ b+2a=-5 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 2b=6 & & \\ b+2a=-5 & & \end{matrix}\right.
\Leftrightarrow \left\{\begin{matrix} b=3 & & \\ b+2a=-5 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} b=3 & & \\ 3+2a=-5 & & \end{matrix}\right.\)
\(\left\{\begin{matrix} 2 - 2b=-4 & & \\ b+2a=-5 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 2b=6 & & \\ b+2a=-5 & & \end{matrix}\right.
\Leftrightarrow \left\{\begin{matrix} b=3 & & \\ b+2a=-5 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} b=3 & & \\ 3+2a=-5 & & \end{matrix}\right.\)
![]() \(\Leftrightarrow \left\{\begin{matrix} b=3 & & \\ 2a = -5 - 3& & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} b=3 & & \\ 2a = -8& & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} b=3 & & \\ 2a = -5 - 3& & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} b=3 & & \\ 2a = -8& & \end{matrix}\right.\)
![]() \(\Leftrightarrow \left\{\begin{matrix} b=3 & & \\ a = -4 & & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} b=3 & & \\ a = -4 & & \end{matrix}\right.\)
Vậy a=-4, b=3 thì hệ có nghiệm là (1; -2).
b) Thay ![]() \(x=\sqrt 2 - 1;\ y= \sqrt 2\) vào hệ phương trình đã cho, ta có:
\(x=\sqrt 2 - 1;\ y= \sqrt 2\) vào hệ phương trình đã cho, ta có:
 \(\left\{\begin{matrix} 2(\sqrt{2}-1)+b\sqrt{2}= -4 & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.
\Leftrightarrow \left\{\begin{matrix} 2\sqrt{2}-2+b\sqrt{2}= -4 & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.\)
\(\left\{\begin{matrix} 2(\sqrt{2}-1)+b\sqrt{2}= -4 & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.
\Leftrightarrow \left\{\begin{matrix} 2\sqrt{2}-2+b\sqrt{2}= -4 & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.\)
 \(\Leftrightarrow \left\{\begin{matrix} 2\sqrt{2}-2+b\sqrt{2}= -4 & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.
\Leftrightarrow \left\{\begin{matrix} b\sqrt{2}= -2 - 2\sqrt{2} & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} 2\sqrt{2}-2+b\sqrt{2}= -4 & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.
\Leftrightarrow \left\{\begin{matrix} b\sqrt{2}= -2 - 2\sqrt{2} & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.\)
 \(\Leftrightarrow \left\{\begin{matrix} b= -(2 + \sqrt{2}) & & \\ a\sqrt{2}= -(2 + \sqrt{2})(\sqrt{2}-1)+5& & \end{matrix}\right.
\Leftrightarrow \left\{\begin{matrix} b= -(2 + \sqrt{2}) & & \\ a\sqrt{2}= -\sqrt{2}+5& & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} b= -(2 + \sqrt{2}) & & \\ a\sqrt{2}= -(2 + \sqrt{2})(\sqrt{2}-1)+5& & \end{matrix}\right.
\Leftrightarrow \left\{\begin{matrix} b= -(2 + \sqrt{2}) & & \\ a\sqrt{2}= -\sqrt{2}+5& & \end{matrix}\right.\)
 \(\Leftrightarrow \left\{\begin{matrix} a = \dfrac{-2+5\sqrt{2}}{2} & & \\ b = -(2+ \sqrt{2})& & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} a = \dfrac{-2+5\sqrt{2}}{2} & & \\ b = -(2+ \sqrt{2})& & \end{matrix}\right.\)
Vậy ![]() \(a = \dfrac{-2+5\sqrt{2}}{2},\ b=-(2+ \sqrt{2})\) thì hệ trên có nghiệm là
\(a = \dfrac{-2+5\sqrt{2}}{2},\ b=-(2+ \sqrt{2})\) thì hệ trên có nghiệm là ![]() \((\sqrt 2 -1; \sqrt 2).\)
\((\sqrt 2 -1; \sqrt 2).\)
Bài 19 (trang 16 SGK Toán 9 Tập 2)
Biết rằng: Đa thức P(x) chia hết cho đa thức x - a khi và chỉ khi P(a) = 0.
Hãy tìm các giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x - 3:
![]() \(P(x) = m{x^3} + (m - 2){x^2} - (3n - 5)x - 4n\)
\(P(x) = m{x^3} + (m - 2){x^2} - (3n - 5)x - 4n\)
+) Ta có: P(x) chia hết cho ![]() \(x + 1 \Leftrightarrow P(-1)=0\)
\(x + 1 \Leftrightarrow P(-1)=0\)
![]() \(\Leftrightarrow m.(-1)^3 + (m - 2).(-1)^2 - (3n - 5).(-1)
- 4n=0\)
\(\Leftrightarrow m.(-1)^3 + (m - 2).(-1)^2 - (3n - 5).(-1)
- 4n=0\)
![]() \(\Leftrightarrow -m + m - 2 + 3n - 5 - 4n = 0
\Leftrightarrow -n-7=0
\Leftrightarrow n+7=0 (1)\)
\(\Leftrightarrow -m + m - 2 + 3n - 5 - 4n = 0
\Leftrightarrow -n-7=0
\Leftrightarrow n+7=0 (1)\)
+) Lại có: P(x) chia hết cho ![]() \(x - 3 \Leftrightarrow P(3)=0\)
\(x - 3 \Leftrightarrow P(3)=0\)
![]() \(\Leftrightarrow m.3^3 + (m - 2).3^2 - (3n - 5).3 - 4n=0\)
\(\Leftrightarrow m.3^3 + (m - 2).3^2 - (3n - 5).3 - 4n=0\)
![]() \(\Leftrightarrow 27m + 9(m - 2) - 3(3n - 5) - 4n = 0\)
\(\Leftrightarrow 27m + 9(m - 2) - 3(3n - 5) - 4n = 0\)
![]() \(\Leftrightarrow 27m + 9m - 18 - 9n + 15 - 4n = 0\)
\(\Leftrightarrow 27m + 9m - 18 - 9n + 15 - 4n = 0\)
![]() \(\Leftrightarrow 36m-13n=3 (2)\)
\(\Leftrightarrow 36m-13n=3 (2)\)
Từ (1) và (2), ta có hệ phương trình ẩn m và n.
![]() \(\left\{\begin{matrix} n+7 = 0 & & \\ 36m - 13n = 3 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} n = -7 & & \\ 36m -13.(-7)= 3 & & \end{matrix}\right.\)
\(\left\{\begin{matrix} n+7 = 0 & & \\ 36m - 13n = 3 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} n = -7 & & \\ 36m -13.(-7)= 3 & & \end{matrix}\right.\)
 \(\Leftrightarrow \left\{\begin{matrix} n = -7 & & \\ 36m = -88 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} n = -7& & \\ m = \dfrac{-22}{9}& & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} n = -7 & & \\ 36m = -88 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} n = -7& & \\ m = \dfrac{-22}{9}& & \end{matrix}\right.\)
Vậy ![]() \(m=\dfrac{-22}{9},\ n=-7.\)
\(m=\dfrac{-22}{9},\ n=-7.\)
Ngoài Giải bài tập SGK Toán lớp 9 bài 3: Giải hệ phương trình bằng phương pháp thế, các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt.








