Giải Toán 9 bài 6: Tính chất của hai tiếp tuyến cắt nhau

Giải bài tập Toán lớp 9 bài 6: Tính chất của hai tiếp tuyến cắt nhau bao gồm đáp án chi tiết cho các câu hỏi trong SGK Toán 9, giúp các em nắm vững kiến thức được học trong bài, từ đó luyện giải Toán 9 hiệu quả.

Lý thuyết Tính chất của hai tiếp tuyến cắt nhau

1. Định lí:

Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

• Điểm đó cách đều 2 tiếp điểm.
• Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
• Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.

2. Đường tròn nội tiếp:

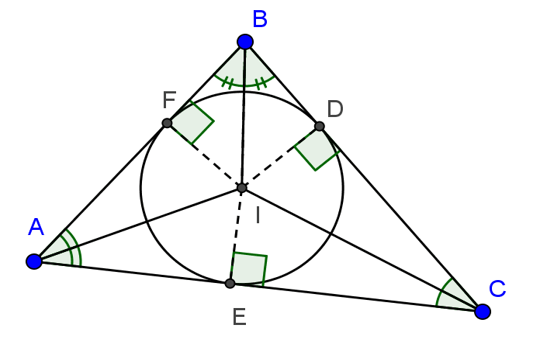
Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, cón tam giác gọi là ngoại tiếp đường tròn.

Tâm đường tròn nội tiếp tam giác là giao ba đường phân giác của tam giác đó.

3. Đường tròn bàng tiếp tam giác

Đường tròn tiếp xúc với một cạnh của một tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia gọi là đường tròn bàng tiếp tam giác.

Tâm của đường tròn bàng tiếp tam giác trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, hoặc là giao điểm của đường phân giác góc A và đường phân giác góc ngoài tại B(hoặc C). Với một tam giác , có ba đường tròn bàng tiếp.

Trả lời câu hỏi Toán 9 Tập 1 Bài 6 trang 113

Cho hình 79 trong đó AB, AC theo thứ tự là các tiếp tuyến tại B, tại C của đường tròn (O). Hãy kể tên một vài đoạn thẳng bằng nhau, một vài góc bằng nhau trong hình.

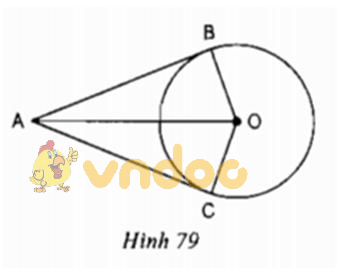
Lời giải

Các đoạn thẳng bằng nhau là: AB = AC; OB = OC

Các góc bằng nhau là: ∠(BAO) = ∠(CAO); ∠(BOA) = ∠(COA)

∠(ABO) = ∠(ACO) = 90^o

Trả lời câu hỏi Toán 9 Tập 1 Bài 6 trang 114

Hãy nêu cách tìm tâm của một miếng gỗ hình tròn bằng “thước phân giác” (xem hình vẽ trong khung ở đầu bài 6).

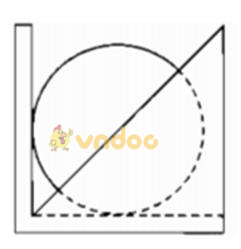
Lời giải

- Ta đặt miếng gỗ hình tròn tiếp xúc với hai cạnh của thước.

- Kẻ theo “tia phân giác“ của thước, ta vẽ được một đường kính của hình tròn

- Xoay miếng gỗ rồi làm tiếp tục như trên, ta được đường kính thứ hai.

- Giao điểm của hai đường kính chính là tâm đường tròn

Trả lời câu hỏi Toán 9 Tập 1 Bài 6 trang 114

Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB (h.80). Chứng minh rằng ba điểm D, E, F nằm trên cùng một đường tròn tâm I.

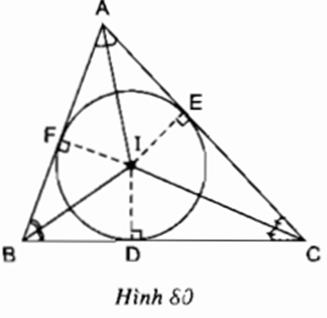
Lời giải

Theo tính chất tia phân giác, ta có:

AI là tia phân giác của góc BAC

⇒ IE = IF

Tương tự: CI là tia phân giác của góc ACB

⇒ IE = ID

Do đó: IE = IF = ID

Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I

Trả lời câu hỏi Toán 9 Tập 1 Bài 6 trang 115

Cho tam giác ABC, K là giao điểm các đường phân giác của hai góc ngoài tại B và C; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ K đến các đường thẳng BC, AC, AB (h.81). Chứng minh rằng ba điểm D, E, F năm trên cùng một đường tròn có tâm K.

Lời giải

Theo tính chất tia phân giác, ta có:

AK là tia phân giác của góc BAC

⇒ KE = KF

Tương tự: CK là tia phân giác của góc ngoài của góc ACB

⇒ KE = KD

Do đó: KE = KF = KD

Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm K

Bài 26 (trang 115 SGK Toán 9 Tập 1)

Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).

a) Chứng minh rằng OA vuông góc với BC.

b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.

c) Tính độ dài các cạnh của tam giác ABC; biết OB = 2cm, OA = 4cm.

Lời giải

Vẽ hình minh họa:

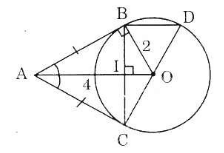
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.

Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)

b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).

Xét ΔCBD có :

CI = IB

CO = OD (bán kính)

⇒ BD//OI (OI là đường trung bình của tam giác BCD).

Vậy BD//AO.

c) Theo định lí Pitago trong tam giác vuông OAC:

AC² = OA² – OC² = 4² – 2² = 12

=> AC = √12 = 2√3 (cm)

Vậy AB=AC=BC= \(2\sqrt{3}\)cm

Nhận xét. Qua câu c) ta thấy: Góc tạo bởi hai tiếp tuyến của một đường tròn vẽ từ một điểm cách tâm một khoảng bằng đường kính đúng bằng \(60^{\circ}\)

Bài 27 (trang 115 SGK Toán 9 Tập 1)

Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.

Lời giải:

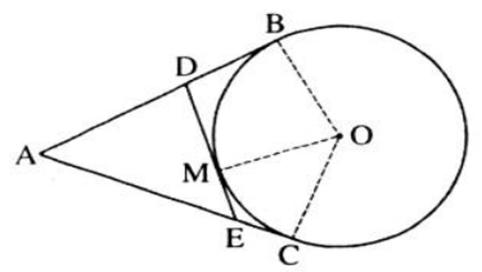
Theo tính chất hai tiếp tuyến cắt nhau ta có:

DM = DB, EM = EC, AB = AC

Chu vi ΔADE:

CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)

Bài 28 (trang 116 SGK Toán 9 Tập 1)

Cho góc xAy khác góc bẹt. Tâm của các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên đường nào?

Lời giải:

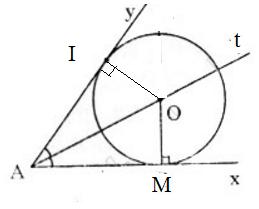
Gọi O là tâm của một đường tròn bất kì tiếp xúc với hai cạnh góc xAy. Theo tính chất của hai tiếp tuyến cắt nhau ta có:

Hay AO là tia phân giác của góc xAy.

Vậy tâm các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên tia phân giác của góc xAy.

Bài 29 (trang 116 SGK Toán 9 Tập 1)

Cho góc xAy khác góc bẹt, điểm B thuộc tia Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.

Lời giải:

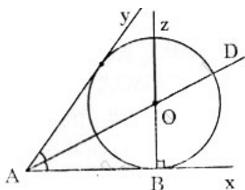
Đường tròn (O) tiếp xúc với hai tia Ax và Ay nên tâm O của (O) nằm trên tia phân giác của góc xAy. Do đó ta có cách dựng:

- Dựng tia phân giác At của góc xAy.

- Dựng đường thẳng Bz qua B và vuông góc với tia Ax.

- Giao điểm O của At và Bz là tâm của đường tròn cần dựng.

- Dựng đường tròn tâm O, bán kính R = OB, ta được đường tròn cần dựng.

Bài 30 (trang 116 SGK Toán 9 Tập 1)

Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng:

a) ∠COD = 90^o

b) CD = AC + BD

c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.

Lời giải:

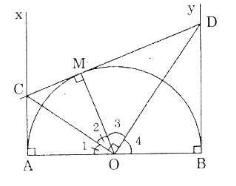
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:

OC là tia phân giác của ∠AOM

OD và tia phân giác của ∠BOM

OC và OD là các tia phân giác của hai góc kề bù ∠AOM và ∠BOM nên OC ⊥ OD.

=> ∠COD = 90^o (đpcm)

b) Theo tính chất của hai tiếp tuyến cắt nhau ta có:

CM = AC, DM = BC

Do đó: CD = CM + DM = AC + BD (đpcm)

c) Ta có: AC = CM, BD = DM nên AC.BD = CM.MD

ΔCOD vuông tại O, ta có:

CM.MD = OM² = R² (R là bán kính đường tròn O).

Vậy AC.BD = R² (không đổi).

Bài 31 (trang 116 SGK Toán 9 Tập 1)

Trên hình 82, tam giác ABC ngoại tiếp đường tròn (O).

a) Chứng minh rằng:

2AD = AB + AC – BC

b) Tìm các hệ thức tương tự như hệ thức ở câu a.

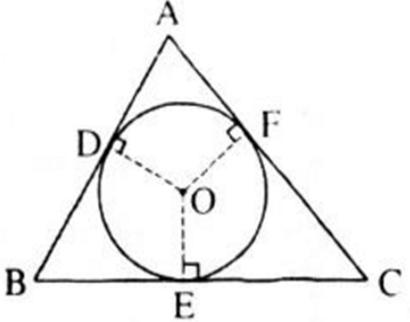
Hình 82

Lời giải:

a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:

BD = BE, CE = CF, AD = AF

Ta có:

AB + AC – BC = (AD + BD) + (AF + FC) – (BE + EC)

= (AD + AF) + (DB – BE) + (FC – EC)

= AD + AF = 2AD.

Vậy 2AD = AB + AC – BC (đpcm)

b) Tương tự ta tìm được các hệ thức:

2BE = BA + BC – AC

2CF = CA + CB – AB

Bài 32 (trang 116 SGK Toán 9 Tập 1)

Cho tam giác đều ABC ngoại tiếp đường tròn bán kính 1cm. Diện tích của tam giác ABC bằng:

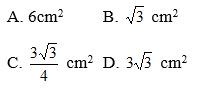
Hãy chọn câu trả lời đúng.

Lời giải:

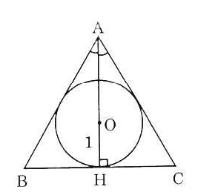
- Chọn D.

- Gọi O là tâm đường tròn nội tiếp Δ ABC, H là tiếp điểm thuộc BC.

Đường phân giác AO của góc A cũng là đường cao nên A, O, H thẳng hàng.

Ta có: HB = BC, ∠HAC = 30^o, AH = 3.OH = 3 (cm)

Trắc nghiệm Tính chất của hai tiếp tuyến cắt nhau

....................................

Ngoài Giải bài tập Toán lớp 9 bài 6: Tính chất của hai tiếp tuyến cắt nhau, mời các bạn tham khảo đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt