Toán 9 Chân trời sáng tạo Bài 3: Tính chất của phép khai phương

Giải Toán 9 Chân trời sáng tạo Bài 3: Tính chất của phép khai phương hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 46, 47, 48, 49, 50, 51, giúp các em nắm vững kiến thức được học trong bài, luyện giải bài tập môn Toán lớp 9.

Giải Toán 9 bài 3: Tính chất của phép khai phương

Giải Toán 9 trang 46
Giải Toán 9 trang 47
Giải Toán 9 trang 48
Giải Toán 9 trang 49
Giải Toán 9 trang 50
Giải Toán 9 trang 51

Giải Toán 9 trang 46

Hoạt động 1 Trang 46 Toán 9 tập 1 Chân trời

Hoàn thành bảng sau vào vở:

a	− 3	3	11	− 11	100	− 100	0
$\sqrt{a^2}$ $\sqrt{a^2}$	3	?	?	?	?	?	?

Từ đó, nhận xét gì về căn bậc hai số học của bình phương của một số?

Hướng dẫn giải:

a	− 3	3	11	− 11	100	− 100	0
$\sqrt{a^2}$ $\sqrt{a^2}$	3	3	11	11	100	100	0

Nhận xét: $\sqrt{a^2}=\left|a\right|$ $\sqrt{a^2}=\left|a\right|$

Giải Toán 9 trang 47

Thực hành 1 Trang 47 Toán 9 tập 1 Chân trời

Tính:

a) $\sqrt{\left(-0,4\right)^2}$ $\sqrt{\left(-0,4\right)^2}$

b) $-\sqrt{\left(-\frac{4}{9}\right)^2}$ $-\sqrt{\left(-\frac{4}{9}\right)^2}$

c) $-2\sqrt{3^2}+\left(-\sqrt{6}\right)^2$ $-2\sqrt{3^2}+\left(-\sqrt{6}\right)^2$

Hướng dẫn giải:

a) $\sqrt{\left(-0,4\right)^2}$ $\sqrt{\left(-0,4\right)^2}$ = |− 0,4| = 0,4

b) $-\sqrt{\left(-\frac{4}{9}\right)^2} =-\left |-\frac{4}{9} \right | =-\frac{4}{9}$ $-\sqrt{\left(-\frac{4}{9}\right)^2} =-\left |-\frac{4}{9} \right | =-\frac{4}{9}$

c) $-2\sqrt{3^2}+\left(-\sqrt{6}\right)^2$ $-2\sqrt{3^2}+\left(-\sqrt{6}\right)^2$ = − 2 . 3 + 6 = 0

Thực hành 2 Trang 47 Toán 9 tập 1 Chân trời

Rút gọn các biểu thức sau:

a) $\sqrt{\left(2-\sqrt{5}\right)^2}$ $\sqrt{\left(2-\sqrt{5}\right)^2}$

b) $\sqrt{a^2}+\sqrt{\left(-3a\right)^2}$ $\sqrt{a^2}+\sqrt{\left(-3a\right)^2}$ với a > 0

Hướng dẫn giải:

a) $\sqrt{\left(2-\sqrt{5}\right)^2}=\left|2-\sqrt{5}\right|=\sqrt{5}-2$ $\sqrt{\left(2-\sqrt{5}\right)^2}=\left|2-\sqrt{5}\right|=\sqrt{5}-2$ (vì $2-\sqrt{5}<0$ $2-\sqrt{5}<0$)

b) $\sqrt{a^2}+\sqrt{\left(-3a\right)^2}$ $\sqrt{a^2}+\sqrt{\left(-3a\right)^2}$ với a > 0

= |a| + |− 3a|

= a + 3a = 4a

Hoạt động 2 trang 47 SGK Toán 9 Chân trời sáng tạo

a) Thực hiện các phép tính cho trên bảng trong Hình 1.

Khám phá 2 trang 47 Toán 9 Tập 1 Chân trời sáng tạo | Giải Toán 9

b) Từ đó, có nhận xét gì về căn bậc hai của tích hai số không âm?

Hướng dẫn giải:

a)

(1) $\sqrt {4.9} = \sqrt {36} = \sqrt {{{\left( 6 \right)}^2}} = 6$ $\sqrt {4.9} = \sqrt {36} = \sqrt {{{\left( 6 \right)}^2}} = 6$

(2) $\sqrt 4 .\sqrt 9 = \sqrt {{2^2}} .\sqrt {{3^2}} = 2.3 = 6$ $\sqrt 4 .\sqrt 9 = \sqrt {{2^2}} .\sqrt {{3^2}} = 2.3 = 6$

(3) $\sqrt {16.25} = \sqrt {400} = \sqrt {{{\left( {20} \right)}^2}} = 20$ $\sqrt {16.25} = \sqrt {400} = \sqrt {{{\left( {20} \right)}^2}} = 20$

(4) $\sqrt {16} .\sqrt {25} = \sqrt {{4^2}} .\sqrt {{5^2}} = 4.5 = 20$ $\sqrt {16} .\sqrt {25} = \sqrt {{4^2}} .\sqrt {{5^2}} = 4.5 = 20$

b) Căn bậc hai của tích hai số không âm bằng tích các căn bậc hai của hai số không âm.

Giải Toán 9 trang 48

Hoạt động 3 trang 48 SGK Toán 9 Chân trời sáng tạo

Thay mỗi ? bằng các số thích hợp:

a) $\sqrt {50} = \sqrt ? .\sqrt 2 = ?.\sqrt 2$ $\sqrt {50} = \sqrt ? .\sqrt 2 = ?.\sqrt 2$

b) $\sqrt {3.{{( - 4)}^2}} = \sqrt ? .\sqrt 3 = ?.\sqrt 3$ $\sqrt {3.{{( - 4)}^2}} = \sqrt ? .\sqrt 3 = ?.\sqrt 3$

c) $3\sqrt 2 = \sqrt ? .\sqrt 2 = \sqrt ?$ $3\sqrt 2 = \sqrt ? .\sqrt 2 = \sqrt ?$

d) $- 2\sqrt 5 = - \sqrt ? .\sqrt 5 = - \sqrt ?$ $- 2\sqrt 5 = - \sqrt ? .\sqrt 5 = - \sqrt ?$

Hướng dẫn giải:

a) $\sqrt {50} = \sqrt {25} .\sqrt 2 = 5.\sqrt 2$ $\sqrt {50} = \sqrt {25} .\sqrt 2 = 5.\sqrt 2$

b) $\sqrt {3.{{( - 4)}^2}} = \sqrt {16} .\sqrt 3 = 4.\sqrt 3$ $\sqrt {3.{{( - 4)}^2}} = \sqrt {16} .\sqrt 3 = 4.\sqrt 3$

c) $3\sqrt 2 = \sqrt 9 .\sqrt 2 = \sqrt {18}$ $3\sqrt 2 = \sqrt 9 .\sqrt 2 = \sqrt {18}$

d) $- 2\sqrt 5 = - \sqrt 4 .\sqrt 5 = - \sqrt 20$ $- 2\sqrt 5 = - \sqrt 4 .\sqrt 5 = - \sqrt 20$

Giải Toán 9 trang 49

Thực hành 3 trang 49 SGK Toán 9 Chân trời sáng tạo

Tính

a) $\sqrt {0,16.64}$ $\sqrt {0,16.64}$

b) $\sqrt {8,{{1.10}^3}}$ $\sqrt {8,{{1.10}^3}}$

c) $\sqrt {12.250.1,2}$ $\sqrt {12.250.1,2}$

d) $\sqrt {28} .\sqrt 7$ $\sqrt {28} .\sqrt 7$

e) $\sqrt {4,9} .\sqrt {30} .\sqrt {12}$ $\sqrt {4,9} .\sqrt {30} .\sqrt {12}$

Hướng dẫn giải:

a) $\sqrt {0,16.64}$ $\sqrt {0,16.64}$ $= \sqrt {0,16} .\sqrt {64}$ $= \sqrt {0,16} .\sqrt {64}$ $= 0,4.8$ $= 3,2$

b) $\sqrt {8,{{1.10}^3}}$ $\sqrt {8,{{1.10}^3}}$ $= \sqrt {81} .\sqrt {{{10}^2}}$ $= \sqrt {81} .\sqrt {{{10}^2}}$ $= 9.10$ $= 90$

c) $\sqrt {12.250.1,2}$ $\sqrt {12.250.1,2}$ $= \sqrt {12.25.10.1,2}$ $= \sqrt {12.25.10.1,2}$ $= \sqrt {12.25.12}$ $= \sqrt {12.25.12}$ $= \sqrt {12.25.12}$ $= \sqrt {12.25.12}$ $= \sqrt {{{25.12}^2}}$ $= \sqrt {{{25.12}^2}}$ $= \sqrt {25} .\sqrt {{{12}^2}}$ $= \sqrt {25} .\sqrt {{{12}^2}}$ $= 5.12$ $= 60$

d) $\sqrt {28} .\sqrt 7$ $\sqrt {28} .\sqrt 7$ $= \sqrt {28.7}$ $= \sqrt {28.7}$ $= \sqrt {4.7.7}$ $= \sqrt {4.7.7}$ $= \sqrt {4} .\sqrt {{{7}^2}}$ $= \sqrt {4} .\sqrt {{{7}^2}}$ $= 2.7$ $= 14$

e) $\sqrt {4,9} .\sqrt {30} .\sqrt {12}$ $\sqrt {4,9} .\sqrt {30} .\sqrt {12}$ $= \sqrt {4,9.30.12}$ $= \sqrt {4,9.30.12}$ $= \sqrt {49.3.12}$ $= \sqrt {49.3.12}$ $= \sqrt {49.36}$ $= \sqrt {49.36}$ $= \sqrt {49} .\sqrt {36}$ $= \sqrt {49} .\sqrt {36}$ $= 7.6$ $= 42$

Thực hành 4 trang 49 SGK Toán 9 Chân trời sáng tạo

Rút gọn các biểu thức sau:

a) $\sqrt {500}$ $\sqrt {500}$

b) $\sqrt {5a} .\sqrt {20a}$ $\sqrt {5a} .\sqrt {20a}$ với a $\ge$ $\ge$0

c) $\sqrt {18.{{\left( {2 - a} \right)}^2}}$ $\sqrt {18.{{\left( {2 - a} \right)}^2}}$ với a > 2

Hướng dẫn giải:

a) $\sqrt {500} = \sqrt {5.100} = \sqrt 5 .\sqrt {100} = 10\sqrt 5$ $\sqrt {500} = \sqrt {5.100} = \sqrt 5 .\sqrt {100} = 10\sqrt 5$

b) $\sqrt {5a} .\sqrt {20a} = \sqrt {5a.20a} = \sqrt {100{a^2}} = \sqrt {100} .\sqrt {{a^2}} = 10a$ $\sqrt {5a} .\sqrt {20a} = \sqrt {5a.20a} = \sqrt {100{a^2}} = \sqrt {100} .\sqrt {{a^2}} = 10a$

c) $\sqrt {18.{{\left( {2 - a} \right)}^2}} = \sqrt {9.2.{{\left( {2 - a} \right)}^2}}$ $\sqrt {18.{{\left( {2 - a} \right)}^2}} = \sqrt {9.2.{{\left( {2 - a} \right)}^2}}$ $= \sqrt 9 .\sqrt 2 .\sqrt {{{\left( {2 - a} \right)}^2}}$ $= \sqrt 9 .\sqrt 2 .\sqrt {{{\left( {2 - a} \right)}^2}}$ $= 3\sqrt 2 .\left| {2 - a} \right| = 3\sqrt 2 (a - 2)$ $= 3\sqrt 2 .\left| {2 - a} \right| = 3\sqrt 2 (a - 2)$

Thực hành 5 trang 49 SGK Toán 9 Chân trời sáng tạo

Đưa thừa số vào trong dấu căn bậc hai:

a) $5.\sqrt 2$ $5.\sqrt 2$

b) $- 10\sqrt 7$ $- 10\sqrt 7$

c) $2a\sqrt {\frac{3}{{10a}}}$ $2a\sqrt {\frac{3}{{10a}}}$ với a > 0

Hướng dẫn giải:

a) $5.\sqrt 2 = \sqrt {{5^2}.2} = \sqrt {50}$ $5.\sqrt 2 = \sqrt {{5^2}.2} = \sqrt {50}$

b) $- 10\sqrt 7 = - \sqrt {{{10}^2}.7} = - \sqrt {700}$ $- 10\sqrt 7 = - \sqrt {{{10}^2}.7} = - \sqrt {700}$

c) $\sqrt {{{\left( {2a} \right)}^2}.\frac{3}{{10a}}} = \sqrt {\frac{{12{a^2}}}{{10a}}} = \sqrt {\frac{{6a}}{5}}$ $\sqrt {{{\left( {2a} \right)}^2}.\frac{3}{{10a}}} = \sqrt {\frac{{12{a^2}}}{{10a}}} = \sqrt {\frac{{6a}}{5}}$.

Vận dụng 1 trang 49 SGK Toán 9 Chân trời sáng tạo

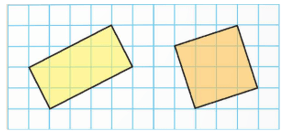
Tính diện tích của hình chữ nhật và hình vuông trong hoạt động khởi động. Biết mỗi ô vuông nhỏ có độ dài cạnh là 1. Diện tích của hai hình đó bằng nhau không?

Vận dụng 1 trang 49 Toán 9 Tập 1 Chân trời sáng tạo | Giải Toán 9

Hướng dẫn giải:

Độ dài chiều dài hình chữ nhật là: $\sqrt {{4^2} + {2^2}} = 2\sqrt 5$ $\sqrt {{4^2} + {2^2}} = 2\sqrt 5$

Độ dài chiều rộng hình chữ nhật là: $\sqrt {{2^2} + {1^2}} = \sqrt 5$ $\sqrt {{2^2} + {1^2}} = \sqrt 5$

Diện tích hình chữ nhật là: $2\sqrt 5 .\sqrt 5 = 2.5 = 10$ $2\sqrt 5 .\sqrt 5 = 2.5 = 10$

Độ dài cạnh hình vuông là: $\sqrt {{3^2} + {1^2}} = \sqrt {10}$ $\sqrt {{3^2} + {1^2}} = \sqrt {10}$

Diện tích hình vuông là: ${\left( {\sqrt {10} } \right)^2} = 10$ ${\left( {\sqrt {10} } \right)^2} = 10$

Vậy diện tích hai hình bằng nhau.

Hoạt động 4 trang 49 SGK Toán 9 Chân trời sáng tạo

a) Thực hiện các phép tính có trên bảng trong Hình 2.

Khám phá 4 trang 49 Toán 9 Tập 1 Chân trời sáng tạo | Giải Toán 9

b) Từ đó, có nhận xét gì về căn bậc hai của thương hai số dương?

Hướng dẫn giải:

a)

(1) $\sqrt {\frac{4}{9}} = \sqrt {{{\left( {\frac{2}{3}} \right)}^2}} = \frac{2}{3}$ $\sqrt {\frac{4}{9}} = \sqrt {{{\left( {\frac{2}{3}} \right)}^2}} = \frac{2}{3}$

(2) $\frac{{\sqrt 4 }}{{\sqrt 9 }} = \frac{{\sqrt {{2^2}} }}{{\sqrt {{3^2}} }} = \frac{2}{3}$ $\frac{{\sqrt 4 }}{{\sqrt 9 }} = \frac{{\sqrt {{2^2}} }}{{\sqrt {{3^2}} }} = \frac{2}{3}$

(3) $\sqrt {\frac{{16}}{{25}}} = \sqrt {{{\left( {\frac{4}{5}} \right)}^2}} = \frac{4}{5}$ $\sqrt {\frac{{16}}{{25}}} = \sqrt {{{\left( {\frac{4}{5}} \right)}^2}} = \frac{4}{5}$

(4) $\frac{{\sqrt {16} }}{{\sqrt {25} }} = \frac{{\sqrt {{4^2}} }}{{\sqrt {{5^2}} }} = \frac{4}{5}$ $\frac{{\sqrt {16} }}{{\sqrt {25} }} = \frac{{\sqrt {{4^2}} }}{{\sqrt {{5^2}} }} = \frac{4}{5}$

b) Căn bậc hai của thương hai số dương bằng thương của căn bậc hai hai số dương.

Giải Toán 9 trang 50

Thực hành 6 trang 50 SGK Toán 9 Chân trời sáng tạo

Tính

a) $\sqrt {\frac{9}{{25}}}$ $\sqrt {\frac{9}{{25}}}$

b) $\sqrt {1\frac{9}{{16}}}$ $\sqrt {1\frac{9}{{16}}}$

c) $\sqrt {150} :\sqrt 6$ $\sqrt {150} :\sqrt 6$

d) $\sqrt {\frac{3}{5}} :\sqrt {\frac{5}{{12}}}$ $\sqrt {\frac{3}{5}} :\sqrt {\frac{5}{{12}}}$

Hướng dẫn giải:

a) $\sqrt {\frac{9}{{25}}} = \frac{{\sqrt 9 }}{{\sqrt {25} }} = \frac{3}{5}$ $\sqrt {\frac{9}{{25}}} = \frac{{\sqrt 9 }}{{\sqrt {25} }} = \frac{3}{5}$

b) $\sqrt {1\frac{9}{{16}}} = \sqrt {\frac{{25}}{{16}}} = \frac{{\sqrt {25} }}{{\sqrt {16} }} = \frac{5}{4}$ $\sqrt {1\frac{9}{{16}}} = \sqrt {\frac{{25}}{{16}}} = \frac{{\sqrt {25} }}{{\sqrt {16} }} = \frac{5}{4}$

c) $\sqrt {150} :\sqrt 6 = \sqrt {\frac{{150}}{6}} = \sqrt {25} = 5$ $\sqrt {150} :\sqrt 6 = \sqrt {\frac{{150}}{6}} = \sqrt {25} = 5$

d) $\sqrt {\frac{3}{5}} :\sqrt {\frac{5}{{12}}} = \sqrt {\frac{3}{5}:\frac{5}{{12}}} = \sqrt {\frac{3}{5}.\frac{{12}}{5}} = \sqrt {\frac{{36}}{{25}}} = \frac{{\sqrt {36} }}{{\sqrt {25} }} = \frac{6}{5}$ $\sqrt {\frac{3}{5}} :\sqrt {\frac{5}{{12}}} = \sqrt {\frac{3}{5}:\frac{5}{{12}}} = \sqrt {\frac{3}{5}.\frac{{12}}{5}} = \sqrt {\frac{{36}}{{25}}} = \frac{{\sqrt {36} }}{{\sqrt {25} }} = \frac{6}{5}$

Thực hành 7 trang 50 SGK Toán 9 Chân trời sáng tạo

Rút gọn các biểu thức sau:

a) $\frac{{\sqrt {555} }}{{\sqrt {111} }}$ $\frac{{\sqrt {555} }}{{\sqrt {111} }}$

b) $\sqrt {\frac{{{a^2}}}{{4{b^4}}}}$ $\sqrt {\frac{{{a^2}}}{{4{b^4}}}}$ với $a \ge 0;b \ne 0$ $a \ge 0;b \ne 0$

c) $\frac{{\sqrt {2{a^2}{{(1 - a)}^2}} }}{{\sqrt {50} }}$ $\frac{{\sqrt {2{a^2}{{(1 - a)}^2}} }}{{\sqrt {50} }}$ với a > 1

Hướng dẫn giải:

a) $\frac{{\sqrt {555} }}{{\sqrt {111} }} = \sqrt {\frac{{555}}{{111}}} = \sqrt 5$ $\frac{{\sqrt {555} }}{{\sqrt {111} }} = \sqrt {\frac{{555}}{{111}}} = \sqrt 5$

b) $\sqrt {\frac{{{a^2}}}{{4{b^4}}}} = \frac{{\sqrt {{a^2}} }}{{\sqrt {4{b^4}} }} = \frac{a}{{2{b^2}}}$ $\sqrt {\frac{{{a^2}}}{{4{b^4}}}} = \frac{{\sqrt {{a^2}} }}{{\sqrt {4{b^4}} }} = \frac{a}{{2{b^2}}}$

c) $\frac{{\sqrt {2{a^2}{{(1 - a)}^2}} }}{{\sqrt {50} }} = \sqrt {\frac{{2{a^2}{{(1 - a)}^2}}}{{50}}} = \sqrt {\frac{{{a^2}{{(1 - a)}^2}}}{{25}}} = \frac{{\sqrt {{a^2}{{(1 - a)}^2}} }}{{\sqrt {25} }} = \frac{{a(a-1)}}{5}$ $\frac{{\sqrt {2{a^2}{{(1 - a)}^2}} }}{{\sqrt {50} }} = \sqrt {\frac{{2{a^2}{{(1 - a)}^2}}}{{50}}} = \sqrt {\frac{{{a^2}{{(1 - a)}^2}}}{{25}}} = \frac{{\sqrt {{a^2}{{(1 - a)}^2}} }}{{\sqrt {25} }} = \frac{{a(a-1)}}{5}$

Vận dụng 2 trang 50 SGK Toán 9 Chân trời sáng tạo

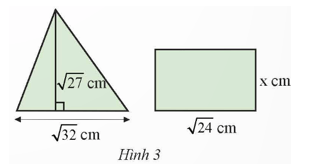
Biết rằng hình tam giác và hình chữ nhật ở Hình 3 có diện tích bằng nhau. Tính chiều rộng x của hình chữ nhật.

Vận dụng 2 trang 50 Toán 9 Tập 1 Chân trời sáng tạo | Giải Toán 9

Hướng dẫn giải:

Diện tích tam giác là: $\frac{1}{2}.\sqrt {27} .\sqrt {32} = \frac{1}{2}.\sqrt {3.9} .\sqrt {16.2} = \frac{1}{2}.3\sqrt 3 .4\sqrt 2 = 6\sqrt 6$ $\frac{1}{2}.\sqrt {27} .\sqrt {32} = \frac{1}{2}.\sqrt {3.9} .\sqrt {16.2} = \frac{1}{2}.3\sqrt 3 .4\sqrt 2 = 6\sqrt 6$ cm²

Suy ra diện tích hình chữ nhật là $6\sqrt 6$ $6\sqrt 6$ cm²

Vậy x = $\frac{{6\sqrt 6 }}{{\sqrt {24} }} = \frac{{6\sqrt 6 }}{{2\sqrt 6 }} = 3$ $\frac{{6\sqrt 6 }}{{\sqrt {24} }} = \frac{{6\sqrt 6 }}{{2\sqrt 6 }} = 3$cm.

Giải Toán 9 trang 51

Bài 1 trang 51 Toán 9 Tập 1

Tính

a) $\sqrt {{{\left( { - 10} \right)}^2}}$ $\sqrt {{{\left( { - 10} \right)}^2}}$

b) $\sqrt {{{\left( { - \frac{2}{7}} \right)}^2}}$ $\sqrt {{{\left( { - \frac{2}{7}} \right)}^2}}$

c) ${\left( { - \sqrt 2 } \right)^2} - \sqrt {25}$ ${\left( { - \sqrt 2 } \right)^2} - \sqrt {25}$

d) ${\left( { - \sqrt {\frac{2}{3}} } \right)^2}.\sqrt {0,09}$ ${\left( { - \sqrt {\frac{2}{3}} } \right)^2}.\sqrt {0,09}$

Hướng dẫn giải

$a) \sqrt {{{\left( { - 10} \right)}^2}} = \left| { - 10} \right| = 10$ $a) \sqrt {{{\left( { - 10} \right)}^2}} = \left| { - 10} \right| = 10$

$b) \sqrt {{{\left( { - \frac{2}{7}} \right)}^2}} = \left| { - \frac{2}{7}} \right| = \frac{2}{7}$ $b) \sqrt {{{\left( { - \frac{2}{7}} \right)}^2}} = \left| { - \frac{2}{7}} \right| = \frac{2}{7}$

$c) {\left( { - \sqrt 2 } \right)^2} - \sqrt {25} = 2 - 5 = - 3$ $c) {\left( { - \sqrt 2 } \right)^2} - \sqrt {25} = 2 - 5 = - 3$

$d) {\left( { - \sqrt {\frac{2}{3}} } \right)^2}.\sqrt {0,09} = \frac{2}{3}.0,3 = 0,2$ $d) {\left( { - \sqrt {\frac{2}{3}} } \right)^2}.\sqrt {0,09} = \frac{2}{3}.0,3 = 0,2$

Bài 2 trang 51 Toán 9 Tập 1

Rút gọn các biểu thức sau:

a) $\sqrt {{{\left( {3 - \sqrt {10} } \right)}^2}}$ $\sqrt {{{\left( {3 - \sqrt {10} } \right)}^2}}$

b) $2\sqrt {{a^2}} + 4a$ $2\sqrt {{a^2}} + 4a$ với a < 0

c) $\sqrt {{a^2}} + \sqrt {{{\left( {3 - a} \right)}^2}}$ $\sqrt {{a^2}} + \sqrt {{{\left( {3 - a} \right)}^2}}$ với 0 < a < 3

Hướng dẫn giải

a) $\sqrt {{{\left( {3 - \sqrt {10} } \right)}^2}} = \left| {3 - \sqrt {10} } \right| = \sqrt {10} - 3$ $\sqrt {{{\left( {3 - \sqrt {10} } \right)}^2}} = \left| {3 - \sqrt {10} } \right| = \sqrt {10} - 3$

b) $2\sqrt {{a^2}} + 4a = 2\left| a \right| + 4a = - 2a + 4a = 2a$ $2\sqrt {{a^2}} + 4a = 2\left| a \right| + 4a = - 2a + 4a = 2a$ với a < 0

c) $\sqrt {{a^2}} + \sqrt {{{\left( {3 - a} \right)}^2}} = \left| a \right| + \left| {3 - a} \right| = a + 3 - a = 3$ $\sqrt {{a^2}} + \sqrt {{{\left( {3 - a} \right)}^2}} = \left| a \right| + \left| {3 - a} \right| = a + 3 - a = 3$ với 0 < a < 3

Bài 3 trang 51 Toán 9 Tập 1

Tính

a) $\sqrt {16.0,25}$ $\sqrt {16.0,25}$

b) $\sqrt {{2^4}.{{( - 7)}^2}}$ $\sqrt {{2^4}.{{( - 7)}^2}}$

c) $\sqrt {0,9} .\sqrt {1000}$ $\sqrt {0,9} .\sqrt {1000}$

d) $\sqrt 2 .\sqrt 5 .\sqrt {40}$ $\sqrt 2 .\sqrt 5 .\sqrt {40}$

Hướng dẫn giải

$a) \sqrt {16.0,25} = \sqrt {16} .\sqrt {0,25} = 4.0,5 = 2$ $a) \sqrt {16.0,25} = \sqrt {16} .\sqrt {0,25} = 4.0,5 = 2$

$b) \sqrt {{2^4}.{{( - 7)}^2}} = \sqrt {{{( - 7)}^2}} .\sqrt {{2^4}} = {7.2^2} = 28$ $b) \sqrt {{2^4}.{{( - 7)}^2}} = \sqrt {{{( - 7)}^2}} .\sqrt {{2^4}} = {7.2^2} = 28$

$c) \sqrt {0,9} .\sqrt {1000} = \sqrt {0,9.1000} = \sqrt {900} = \sqrt {{{30}^2}} = 30$ $c) \sqrt {0,9} .\sqrt {1000} = \sqrt {0,9.1000} = \sqrt {900} = \sqrt {{{30}^2}} = 30$

$d) \sqrt 2 .\sqrt 5 .\sqrt {40} = \sqrt {2.5.40} = \sqrt {400} = \sqrt {{{20}^2}} = 20$ $d) \sqrt 2 .\sqrt 5 .\sqrt {40} = \sqrt {2.5.40} = \sqrt {400} = \sqrt {{{20}^2}} = 20$

Bài 4 trang 51 Toán 9 Tập 1

Rút gọn các biểu thức sau:

a) $\sqrt {{8^2}.5}$ $\sqrt {{8^2}.5}$

b) $\sqrt {81{a^2}}$ $\sqrt {81{a^2}}$với a < 0

c) $\sqrt {5a} .\sqrt {45a} - 3a$ $\sqrt {5a} .\sqrt {45a} - 3a$ với $a \ge 0$ $a \ge 0$

Hướng dẫn giải

a) $\sqrt {{8^2}.5} = \sqrt {{8^2}} .\sqrt 5 = 8\sqrt 5$ $\sqrt {{8^2}.5} = \sqrt {{8^2}} .\sqrt 5 = 8\sqrt 5$

b) $\sqrt {81{a^2}} = \sqrt {{{\left( {9a} \right)}^2}} = - 9a$ $\sqrt {81{a^2}} = \sqrt {{{\left( {9a} \right)}^2}} = - 9a$ với a < 0

c) $\sqrt {5a} .\sqrt {45a} - 3a = \sqrt {5.45a.a} - 3a = \sqrt {225{a^2}} - 3a = 15a - 3a = 12a$ $\sqrt {5a} .\sqrt {45a} - 3a = \sqrt {5.45a.a} - 3a = \sqrt {225{a^2}} - 3a = 15a - 3a = 12a$ với $a \ge 0$ $a \ge 0$

Bài 5 trang 51 Toán 9 Tập 1

Tính

a) $\sqrt {\frac{{0,49}}{{81}}}$ $\sqrt {\frac{{0,49}}{{81}}}$

b) $\sqrt {2\frac{7}{9}}$ $\sqrt {2\frac{7}{9}}$

c) $\sqrt {\frac{1}{{16}}.\frac{9}{{36}}}$ $\sqrt {\frac{1}{{16}}.\frac{9}{{36}}}$

d) $\left( { - \sqrt {52} } \right):\sqrt {13}$ $\left( { - \sqrt {52} } \right):\sqrt {13}$

Hướng dẫn giải

$a) \sqrt {\frac{{0,49}}{{81}}} = \frac{{\sqrt {0,49} }}{{\sqrt {81} }} = \frac{{0,7}}{9} = \frac{7}{{90}}$ $a) \sqrt {\frac{{0,49}}{{81}}} = \frac{{\sqrt {0,49} }}{{\sqrt {81} }} = \frac{{0,7}}{9} = \frac{7}{{90}}$

$b) \sqrt {2\frac{7}{9}} = \sqrt {\frac{{25}}{9}} = \frac{{\sqrt {25} }}{{\sqrt 9 }} = \frac{5}{3}$ $b) \sqrt {2\frac{7}{9}} = \sqrt {\frac{{25}}{9}} = \frac{{\sqrt {25} }}{{\sqrt 9 }} = \frac{5}{3}$

$c) \sqrt {\frac{1}{{16}}.\frac{9}{{36}}} = \sqrt {\frac{1}{{16}}} .\sqrt {\frac{9}{{36}}} = \frac{1}{4}.\frac{{\sqrt 9 }}{{\sqrt {36} }} = \frac{1}{4}.\frac{3}{6} = \frac{3}{{24}} = \frac{1}{8}$ $c) \sqrt {\frac{1}{{16}}.\frac{9}{{36}}} = \sqrt {\frac{1}{{16}}} .\sqrt {\frac{9}{{36}}} = \frac{1}{4}.\frac{{\sqrt 9 }}{{\sqrt {36} }} = \frac{1}{4}.\frac{3}{6} = \frac{3}{{24}} = \frac{1}{8}$

$d) \left( { - \sqrt {52} } \right):\sqrt {13} = - \frac{{\sqrt {52} }}{{\sqrt {13} }} = - \sqrt {\frac{{52}}{{13}}} = - \sqrt 4 = - 2$ $d) \left( { - \sqrt {52} } \right):\sqrt {13} = - \frac{{\sqrt {52} }}{{\sqrt {13} }} = - \sqrt {\frac{{52}}{{13}}} = - \sqrt 4 = - 2$

Bài 6 trang 51 Toán 9 Tập 1

Rút gọn các biểu thức sau:

a) $\frac{{\sqrt 5 .\sqrt 6 }}{{\sqrt {10} }}$ $\frac{{\sqrt 5 .\sqrt 6 }}{{\sqrt {10} }}$

b) $\frac{{\sqrt {24{a^3}} }}{{\sqrt {6a} }}$ $\frac{{\sqrt {24{a^3}} }}{{\sqrt {6a} }}$ với a > 0

c) $\sqrt {\frac{{3{a^2}b}}{{27}}}$ $\sqrt {\frac{{3{a^2}b}}{{27}}}$ với $a \le 0;b \ge 0$ $a \le 0;b \ge 0$

Hướng dẫn giải

a) $\frac{{\sqrt 5 .\sqrt 6 }}{{\sqrt {10} }} = \frac{{\sqrt {30} }}{{\sqrt {10} }} = \sqrt {\frac{{30}}{{10}}} = \sqrt 3$ $\frac{{\sqrt 5 .\sqrt 6 }}{{\sqrt {10} }} = \frac{{\sqrt {30} }}{{\sqrt {10} }} = \sqrt {\frac{{30}}{{10}}} = \sqrt 3$

b) $\frac{{\sqrt {24{a^3}} }}{{\sqrt {6a} }} = \sqrt {\frac{{24{a^3}}}{{6a}}} = \sqrt {4{a^2}} = 2a$ $\frac{{\sqrt {24{a^3}} }}{{\sqrt {6a} }} = \sqrt {\frac{{24{a^3}}}{{6a}}} = \sqrt {4{a^2}} = 2a$ với a > 0

c) $\sqrt {\frac{{3{a^2}b}}{{27}}} = \sqrt {\frac{{{a^2}b}}{9}} = \frac{{\sqrt {{a^2}b} }}{{\sqrt 9 }} = \frac{{ - a\sqrt b }}{3}$ $\sqrt {\frac{{3{a^2}b}}{{27}}} = \sqrt {\frac{{{a^2}b}}{9}} = \frac{{\sqrt {{a^2}b} }}{{\sqrt 9 }} = \frac{{ - a\sqrt b }}{3}$ với $a \le 0;b \ge 0$ $a \le 0;b \ge 0$

Bài 7 trang 51 Toán 9 Tập 1

Cho hình chữ nhật có chiều rộng a (cm), chiều dài b (cm) và diện tích S (cm²)

a) Tìm S, biết $a = \sqrt 8 ; b = \sqrt {32} .$ $a = \sqrt 8 ; b = \sqrt {32} .$

b) Tìm b, biết $S = 3\sqrt 2 ; a = 2\sqrt 3$ $S = 3\sqrt 2 ; a = 2\sqrt 3$

Hướng dẫn giải

a) Ta có $S = a.b = \sqrt 8 .\sqrt {32} = \sqrt {8.32} = \sqrt {256}$ $S = a.b = \sqrt 8 .\sqrt {32} = \sqrt {8.32} = \sqrt {256}$ = 16 cm²

b) $b = \frac{S}{a} = \frac{{3\sqrt 2 }}{{2\sqrt 3 }} = \sqrt {\frac{{18}}{{12}}} = \sqrt {\frac{3}{2}} = \frac{{\sqrt 6 }}{2} cm$ $b = \frac{S}{a} = \frac{{3\sqrt 2 }}{{2\sqrt 3 }} = \sqrt {\frac{{18}}{{12}}} = \sqrt {\frac{3}{2}} = \frac{{\sqrt 6 }}{2} cm$

Bài 8 trang 51 Toán 9 Tập 1

Từ một tấm thép hình vuông, người thợ cắt hai mảnh hình vuông có diện tích lần lượt là 24 cm² và 40 cm² như Hình 4. Tính diện tích phần còn lại của tấm thép.

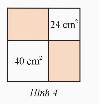
Hướng dẫn giải

Cạnh của hình vuông có diện tích 24 cm² là: $\sqrt {24} = \sqrt {4.6} = 2\sqrt 6 cm$ $\sqrt {24} = \sqrt {4.6} = 2\sqrt 6 cm$

Cạnh của hình vuông có diện tích 40 cm² là: $\sqrt {40} = \sqrt {4.10} = 2\sqrt {10} cm$ $\sqrt {40} = \sqrt {4.10} = 2\sqrt {10} cm$

Diện tích phần còn lại của tấm thép là: $2.2\sqrt 6 .2\sqrt {10} = 8\sqrt {60}$ $2.2\sqrt 6 .2\sqrt {10} = 8\sqrt {60}$cm².

Bài 9 trang 51 Toán 9 Tập 1

Tìm chỗ sai trong phép chứng minh “voi con nặng bằng voi mẹ” sau đây:

$\begin{array}{l}{M^2} - 2Mm + {m^2} = {m^2} - 2mM + {M^2}\\{(M - m)^2} = {(m - M)^2}\\\sqrt {{{(M - m)}^2}} = \sqrt {{{(m - M)}^2}} \\M - m = m - M\\2M = 2m\\M = m(!)\end{array}$ $\begin{array}{l}{M^2} - 2Mm + {m^2} = {m^2} - 2mM + {M^2}\\{(M - m)^2} = {(m - M)^2}\\\sqrt {{{(M - m)}^2}} = \sqrt {{{(m - M)}^2}} \\M - m = m - M\\2M = 2m\\M = m(!)\end{array}$

Hướng dẫn giải

Phép chứng minh trên sai khi đưa thừa số ra ngoài dấu căn.

Từ $\sqrt{{{(M-m)}^{2}}}=\sqrt{{{(m-M)}^{2}}}$ $\sqrt{{{(M-m)}^{2}}}=\sqrt{{{(m-M)}^{2}}}$ ta chỉ có $\left| M-m \right|=\left| m-M \right|$ $\left| M-m \right|=\left| m-M \right|$ chứ không thể có M-m=m-M được.

Chia sẻ, đánh giá bài viết

1

42

Bài trước

Bài sau