Toán 9 Chân trời sáng tạo Bài 2: Tiếp tuyến của đường tròn
Giải Toán 9 Chân trời sáng tạo Bài 2: Tiếp tuyến của đường tròn hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 83, 84, 85, 86, 87, 88.
Toán 9 Chân trời sáng tạo tập 1 trang 83, 84, 85, 86, 87, 88
Giải Toán 9 trang 83
Khám phá 1 trang 83 Toán 9 Tập 1 CTST
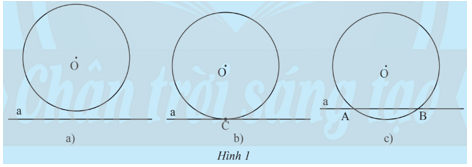
Nêu nhận xét về số điểm chung của đường thẳng a và đường tròn (O) trong mỗi hình sau:
Hướng dẫn giải
⦁ Hình 1a): đường thẳng a và đường tròn (O) không có điểm chung.
⦁ Hình 1b): đường thẳng a và đường tròn (O) có một điểm chung là điểm C.
⦁ Hình 1c): đường thẳng a và đường tròn (O) có hai điểm chung là điểm A và B.
Giải Toán 9 trang 85
Thực hành 1 trang 85 Toán 9 Tập 1 CTST
Cho đường tròn (J; 5 cm) và đường thẳng c. Gọi K là chân đường vuông góc vẽ từ J xuống c, d là độ dài của đoạn thẳng JK. Xác định vị trí tương đối của đường thẳng c và đường tròn (J; 5 cm) trong mỗi trường hợp sau:
a) d = 4 cm;
b) d = 5 cm;
c) d = 6 cm.
Hướng dẫn giải
a)
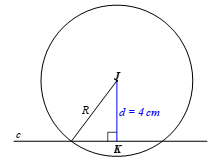
Ta có d = 4 cm, R = 5 cm.
Vì d < R nên đường thẳng c cắt đường tròn (J; 5 cm) tại hai điểm.
b)
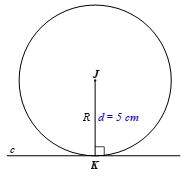
Ta có d = 5 cm, R = 5 cm.
Vì d = R nên đường thẳng c tiếp xúc với đường tròn (J; 5 cm) tại điểm K.
c)
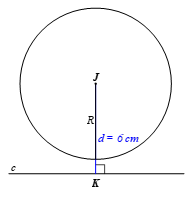
Ta có d = 6 cm, R = 5 cm.
Vì d > R nên đường thẳng c và đường tròn (J; 5 cm) không giao nhau.
Vận dụng 1 trang 85 Toán 9 Tập 1 CTST
Một diễn viên xiếc đi xe đạp một bánh trên sợi dây cáp căng được cố định ở hai đầu dây. Biết đường kính bánh xe là 72 cm, tính khoảng cách từ trục bánh xe đến dây cáp.

Hướng dẫn giải
Do sợi dây tiếp xúc với bánh xe nên khoảng cách từ trục bánh xe đến dây cáp bằng bán kính bánh xe.
Vậy khoảng cách từ trục bánh xe đến dây cáp là: R=![]() \(\frac{72}{2}\)=36 (cm).
\(\frac{72}{2}\)=36 (cm).
Khám phá 2 trang 85 Toán 9 Tập 1 CTST
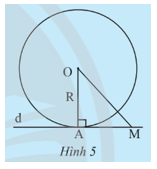
Cho điểm A nằm trên đường tròn (O; R), đường thẳng d đi qua A và vuông góc với OA. Gọi M là một điểm trên d (M khác A).
a) Giải thích tại sao ta có OA = R và OM > R.
b) Giải thích tại sao d và (O) không thể có điểm chung nào khác ngoài A.
Hướng dẫn giải
a) Vì điểm A nằm trên đường tròn (O; R) nên OA = R.
Ta có OA vuông góc với đường thẳng d tại A nên OA là khoảng cách từ điểm O đến đường thẳng d.
Do OA, OM lần lượt là đường vuông góc, đường xiên kẻ từ O đến đường thẳng d nên OA < OM.
Mà OA = R nên OM > R.
b) Ta có OA = R nên d tiếp xúc với đường tròn (O; R) tại A.
Mà khi đường thẳng d tiếp xúc với đường tròn (O; R) thì đường thẳng d và đường tròn (O; R) có duy nhất một điểm chung.
Vậy d và (O) không thể có điểm chung nào khác ngoài A.
Giải Toán 9 trang 86
Thực hành 2 trang 86 Toán 9 Tập 1 CTST
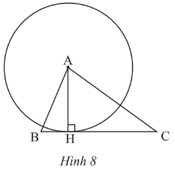
Cho tam giác ABC có đường cao AH (Hình 8). Tìm tiếp tuyến của đường tròn (A; AH) tại H.
Hướng dẫn giải
Ta có BC đi qua H thuộc đường tròn (A; AH) và BC ⊥ AH nên BC là tiếp tuyến của đường tròn (A; AH).
Vận dụng 2 trang 86 Toán 9 Tập 1 CTST
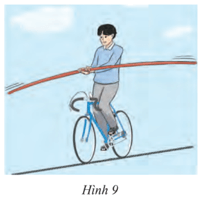
Một diễn viên xiếc đi xe đạp trên một sợi dây cáp căng (Hình 9). Ta coi sợi dây là tiếp tuyến của mỗi bánh xe, xác định các tiếp điểm.
Hướng dẫn giải
Tiếp điểm là giao điểm của mỗi nan hoa với dây cáp.
Giải Toán 9 trang 88
Thực hành 4 trang 88 Toán 9 Tập 1 CTST
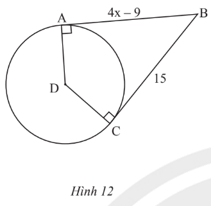
Tìm giá trị của x trong Hình 12.
Hướng dẫn giải
Ta có BA, BC là hai tiếp tuyến của đường tròn (D) cắt nhau tại B nên BA = BC hay 4x – 9 = 15, suy ra 4x = 24 nên x = 6.
Bài 1 trang 88 Toán 9 Tập 1 CTST
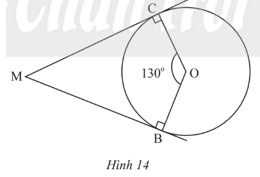
Trong Hình 14, MB, MC lần lượt là tiếp tuyến của đường tròn (O) tại B, C; ![]() \(\widehat {COB}\) =130. Tính số đo
\(\widehat {COB}\) =130. Tính số đo ![]() \(\widehat {CMB}\)
\(\widehat {CMB}\)
Bài 2 trang 88 Toán 9 Tập 1 CTST
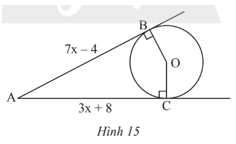
Quan sát Hình 15. Biết AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B, C. Tính giá trị của x.
Hướng dẫn giải
Ta có AB, AC là hai tiếp tuyến của đường tròn (O) cắt nhau tại A nên AB = AC hay 7x – 4 = 3x + 8.
Giải phương trình:
7x – 4 = 3x + 8
4x = 12
x = 3.
Vậy x = 3.
Bài 3 trang 89 Toán 9 Tập 1 CTST
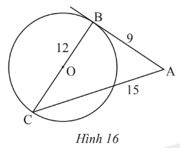
Trong Hình 16, AB = 9, BC = 12, AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O).
Hướng dẫn giải
Xét ∆ABC có:
⦁ AB2 + BC2 = 92 + 122 = 225;
⦁ AC2 = 152 = 225.
Do đó AB2 + BC2 = AC2,
Theo định lí Pythagore đảo, ta có ∆ABC vuông tại B.
Suy ra AB ⊥ BC hay AB ⊥ OB.
Xét đường tròn (O) có AB ⊥ OB tại B thuộc đường tròn (O) nên AB là tiếp tuyến của đường tròn (O).
Bài 4 trang 89 Toán 9 Tập 1 CTST
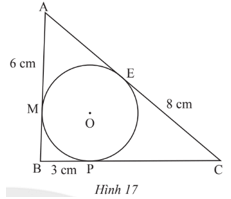
Cho tam giác ABC có đường tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm, BP = 3 cm, CE = 8 cm (Hình 17). Tính chu vi tam giác ABC.
Hướng dẫn giải
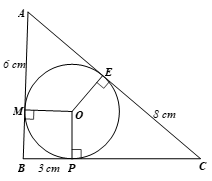
Ta có:
⦁ AE, AM là hai tiếp tuyến của (O) cắt nhau tại A nên AE = AM = 6 cm (tính chất hai tiếp tuyến cắt nhau).
⦁ BM, BP là hai tiếp tuyến của (O) cắt nhau tại B nên BM = BP = 3 cm (tính chất hai tiếp tuyến cắt nhau).
⦁ CP, CE là hai tiếp tuyến của (O) cắt nhau tại C nên CP = CE = 8 cm (tính chất hai tiếp tuyến cắt nhau).
Chu vi tam giác ABC là:
AB + BC + CA = AM + BM + BP + CP + CE + AE
= 6 + 3 + 3 + 8 + 8 + 6 = 34 (cm).
Bài 8 trang 89 Toán 9 Tập 1 CTST
Trong Hình 18, AB là tiếp tuyến của đường tròn (O) tại B.
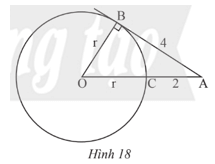
a) Tính bán kính r của đường tròn (O).
b) Tính chiều dài cạnh OA của tam giác ABO.
Hướng dẫn giải
a) Vì AB là tiếp tuyến của đường tròn (O) tại B nên AB ⊥ OB tại B.
Xét ∆OAB vuông tại B, theo định lí Pythagore, ta có: OA2 = OB2 + AB2
Suy ra (OC + CA)2 = OB2 + AB2
Do đó (r + 2)2 = r2 + 42. (*)
Giải phương trình (*):
(r + 2)2 = r2 + 42
r2 + 4r + 4 = r2 + 16
4r = 12
r = 3.
Vậy bán kính của đường tròn (O) là r = 3.
b) Ta có OA = OC + CA = r + 2 = 3 + 2 = 5 (cm).
Vậy OA = 5 cm.









