Giải Toán 9 trang 50 tập 1 Chân trời sáng tạo

Giải Toán 9 trang 50 Tập 1 Chân trời

Thực hành 6 Trang 50 Toán 9 tập 1 Chân trời
Thực hành 7 Trang 50 Toán 9 tập 1 Chân trời
Vận dụng 2 Trang 50 Toán 9 tập 1 Chân trời

Giải Toán 9 trang 50 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 50.

Thực hành 6 Trang 50 Toán 9 tập 1 Chân trời

Tính:

a) $\sqrt{\frac{9}{25}}$ $\sqrt{\frac{9}{25}}$

b) $\sqrt{1\frac{9}{16} }$ $\sqrt{1\frac{9}{16} }$

c) $\sqrt{150} : \sqrt{6}$ $\sqrt{150} : \sqrt{6}$

d) $\sqrt{\frac{3}{5} }: \sqrt{\frac{5}{12} }$ $\sqrt{\frac{3}{5} }: \sqrt{\frac{5}{12} }$

Hướng dẫn giải:

a) $\sqrt{\frac{9}{25}}=\frac{\sqrt{9}}{\sqrt{25}}=\frac{3}{5}$ $\sqrt{\frac{9}{25}}=\frac{\sqrt{9}}{\sqrt{25}}=\frac{3}{5}$

b) $\sqrt{1\frac{9}{16}}=\sqrt{\frac{25}{16}}=\frac{\sqrt{25}}{\sqrt{16}}=\frac{5}{4}$ $\sqrt{1\frac{9}{16}}=\sqrt{\frac{25}{16}}=\frac{\sqrt{25}}{\sqrt{16}}=\frac{5}{4}$

c) $\sqrt{150}:\sqrt{6}=\sqrt{150:6}=\sqrt{25}=5$ $\sqrt{150}:\sqrt{6}=\sqrt{150:6}=\sqrt{25}=5$

d) $\sqrt{\frac{3}{5} }: \sqrt{\frac{5}{12} } =\sqrt{\frac{3}{5}: {\frac{5}{12} } }$ $\sqrt{\frac{3}{5} }: \sqrt{\frac{5}{12} } =\sqrt{\frac{3}{5}: {\frac{5}{12} } }$

$=\sqrt{\frac{36}{25} } =\frac{\sqrt{36}}{\sqrt{25}} = \frac{6}{ 5}$ $=\sqrt{\frac{36}{25} } =\frac{\sqrt{36}}{\sqrt{25}} = \frac{6}{ 5}$

Thực hành 7 Trang 50 Toán 9 tập 1 Chân trời

Rút gọn các biểu thức sau:

a) $\frac{\sqrt{555}}{\sqrt{111}}$ $\frac{\sqrt{555}}{\sqrt{111}}$

b) $\sqrt{\frac{a^2}{4b^4}}$ $\sqrt{\frac{a^2}{4b^4}}$ với a ≥ 0, b ≠ 0

c) $\frac{\sqrt{2a^2\left(1-a\right)^2}}{\sqrt{50}}$ $\frac{\sqrt{2a^2\left(1-a\right)^2}}{\sqrt{50}}$ với a > 1

Hướng dẫn giải:

a) $\frac{\sqrt{555}}{\sqrt{111}}=\sqrt{\frac{555}{111}}=\sqrt{5}$ $\frac{\sqrt{555}}{\sqrt{111}}=\sqrt{\frac{555}{111}}=\sqrt{5}$

b) $\sqrt{\frac{a^2}{4b^4}}=\frac{\sqrt{a^2}}{\sqrt{4b^4}}=\frac{\left|a\right|}{\left|2b^2\right|}=\frac{a}{2b^2}$ $\sqrt{\frac{a^2}{4b^4}}=\frac{\sqrt{a^2}}{\sqrt{4b^4}}=\frac{\left|a\right|}{\left|2b^2\right|}=\frac{a}{2b^2}$ vì a ≥ 0, b ≠ 0

c) $\frac{\sqrt{2a^2\left(1-a\right)^2}}{\sqrt{50}}=\sqrt{\frac{2a^2\left(1-a\right)^2}{50}}$ $\frac{\sqrt{2a^2\left(1-a\right)^2}}{\sqrt{50}}=\sqrt{\frac{2a^2\left(1-a\right)^2}{50}}$

$=\sqrt{\frac{a^2\left(1-a\right)^2}{25}}=\frac{\sqrt{a^2\left(1-a\right)^2}}{\sqrt{25}}$ $=\sqrt{\frac{a^2\left(1-a\right)^2}{25}}=\frac{\sqrt{a^2\left(1-a\right)^2}}{\sqrt{25}}$

$=\frac{\left|a\left(1-a\right)\right|}{5}=\frac{a\left(a-1\right)}{5}$ $=\frac{\left|a\left(1-a\right)\right|}{5}=\frac{a\left(a-1\right)}{5}$ vì a > 1

Vận dụng 2 Trang 50 Toán 9 tập 1 Chân trời

Biết rằng hình tam giác và hình chữ nhật ở Hình 3 có diện tích bằng nhau. Tính chiều rộng x của hình chữ nhật.

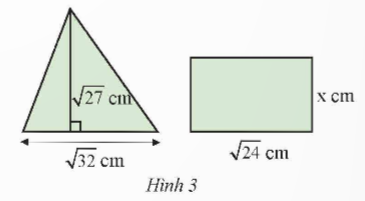
Hướng dẫn giải:

Diện tích hình tam giác là: $\frac{\sqrt{27}.\sqrt{32}}{2}=\frac{\sqrt{27.32}}{2}=\frac{\sqrt{864}}{2}$ $\frac{\sqrt{27}.\sqrt{32}}{2}=\frac{\sqrt{27.32}}{2}=\frac{\sqrt{864}}{2}$ (cm²)

Diện tích hình chữ nhật là: $x\sqrt{24}$ $x\sqrt{24}$ (cm²)

Do hai hình có diện tích bằng nhau nên

$x\sqrt{24}=\frac{\sqrt{864}}{2}$ $x\sqrt{24}=\frac{\sqrt{864}}{2}$

$x=\frac{\sqrt{864}}{2\sqrt{24}}=3$ $x=\frac{\sqrt{864}}{2\sqrt{24}}=3$

Vậy chiều rộng của hình chữ nhật là 3 cm.

----------------------------------------------

---> Xem thêm: Giải Toán 9 trang 51 tập 1 Chân trời sáng tạo

Lời giải Toán 9 trang 50 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 3: Tính chất của phép khai phương, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

49

Bài trước