Giải Toán 9 trang 73 tập 1 Chân trời sáng tạo

Giải Toán 9 trang 73 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 73.

Bài 9 Trang 73 Toán 9 tập 1 Chân trời

Hướng dẫn giải:

a) sin α = 0,25 suy ra α ≈ 14^o 29'

b) cos α = 0,75 suy ra α ≈ 41^o 25'

c) tan α = 1 suy ra α = 45^o

d) cot α = 2 suy ra α ≈ 0^o 1'

Bài 10 Trang 73 Toán 9 tập 1 Chân trời

Hướng dẫn giải:

Xét tam giác ABC vuông tại A, ta có:

BC² = AB² + AC² = 18² + 24² = 900

⇒ BC = 30 cm

$\sin B=\cos C=\frac{AC}{BC}=\frac{24}{30}=\frac{4}{5}$

$\cos B=\sin C=\frac{AB}{BC}=\frac{18}{30}=\frac{3}{5}$

$\tan B=\cot C=\frac{AC}{AB}=\frac{24}{18}=\frac{4}{3}$

$\cot B=\tan C=\frac{AB}{AC}=\frac{18}{24}=\frac{3}{4}$

Bài 11 Trang 73 Toán 9 tập 1 Chân trời

Hướng dẫn giải:

Xét tam giác ABC vuông tại A, ta có:

AC = BC . sin B

AB = BC . sin C

Do đó $\frac{AC}{AB}=\frac{\sin B}{\sin C}$

Bài 12 Trang 73 Toán 9 tập 1 Chân trời

Hướng dẫn giải:

Ta có: sin α = 0,8 ⇒ α ≈ 53^o 7'

Vậy cos α = cos 53^o 7' ≈ 0,6

tan α = tan 53^o 7' ≈ 1,3

cos α = cos 53^o 7' ≈ 0,75

Bài 13 Trang 73 Toán 9 tập 1 Chân trời

Hướng dẫn giải:

a) A = 4 – sin² 45^o + 2cos² 60^o – 3cot³ 45^o

$=4-{\left(\frac{\sqrt{2}}{2}\right)}^2+2.{\left(\frac{1}{2}\right)}^2-{3.1}^3$

$=4-\frac{1}{2}+\frac{1}{2}-3$

= 1

b) B = tan 45^o . cos 30^o . cot 30^o

$=1.\frac{\sqrt{3}}{2}.\sqrt{3}=\frac{3}{2}$

c) C = sin 15^o + sin 75^o – cos 15^o – cos 75^o + sin 30^o

= cos 75^o + cos 15^o – cos 15^o – cos 75^o + sin 30^o

= sin 30^o = $\frac{1}{2}$

Bài 14 Trang 73 Toán 9 tập 1 Chân trời

Hướng dẫn giải:

Xét tam giác OPQ vuông tại O, ta có:

$\hat{Q}={90}^{\circ }-\hat{P}={90}^{\circ }-{39}^{\circ }={51}^{\circ }$

OQ = PQ . sin P = 10 . sin 39^o ≈ 6,3 cm

OP = PQ . sin Q = 10 . sin 51^o ≈ 7,8 cm

Bài 15 Trang 73 Toán 9 tập 1 Chân trời

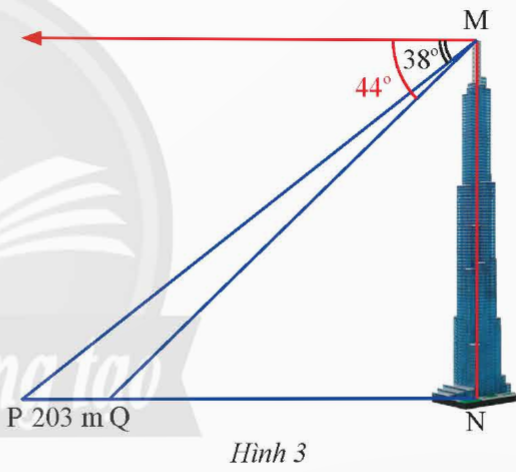
Hướng dẫn giải:

Bài 16 Trang 73 Toán 9 tập 1 Chân trời

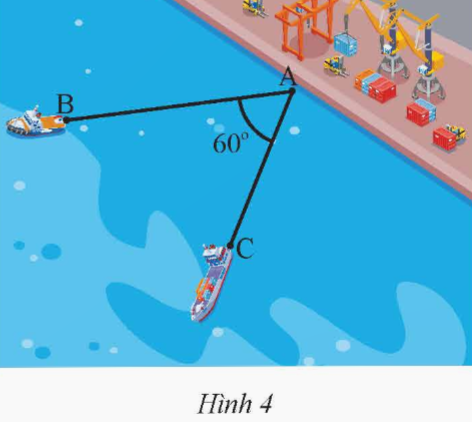
Hướng dẫn giải:

----------------------------------------------

---> Xem thêm: Giải Toán 9 trang 75 tập 1 Chân trời sáng tạo

Lời giải Toán 9 trang 73 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài tập cuối chương 4, được VnDoc biên soạn và đăng tải!