Giải Toán 9 trang 62 tập 1 Chân trời sáng tạo
Giải Toán 9 trang 62 Tập 1 Chân trời
Giải Toán 9 trang 62 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 62.
Hoạt động 2 Trang 62 Toán 9 tập 1 Chân trời
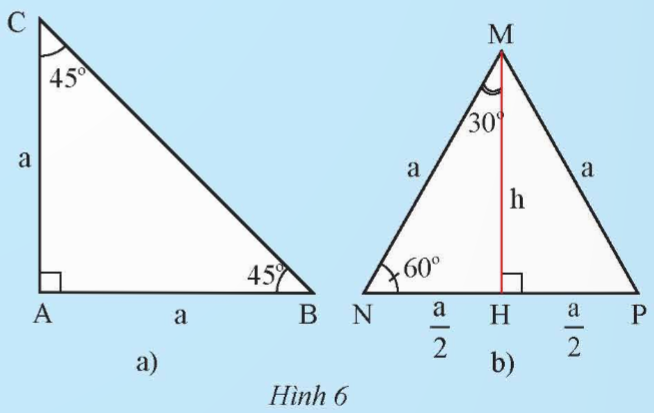
a) Cho tam giác ABC vuông cân tại A có cạnh góc vuông bằng a (Hình 6a). Tính độ dài cạnh huyền BC theo a, rồi tính các tỉ số lượng giác của góc 45o.
b) Cho tam giác đều MNP có cạnh bằng a (Hình 6b). Tính độ dài đường cao MH theo a, rồi tính các tỉ số lượng giác của góc 30o và góc 60o.
Hướng dẫn giải:
a) Xét tam giác ABC vuông tại A:
Ta có: BC2 = AB2 + AC2 = a2 + a2 = 2a2
Suy ra BC = 
\(a\sqrt{2}\)
\(\sin45^{\circ} =\cos45^{\circ} =\frac{a}{a\sqrt{2}}=\frac{\sqrt{2}}{2}\)
\(\tan45^{\circ} =\cot45^{\circ} =\frac{a}{a}=1\)
b) Xét tam giác MNH vuông tại H:
Ta có: MH2 = MN2 - NH2 = \(a^2-\frac{a^2}{4}=\frac{3a^2}{4}\)
Suy ra \(MH=\frac{a\sqrt{3}}{2}\)
\(\sin30^{\circ} =\frac{NH}{MN}=\frac{ 1}{ 2}; \cos30^{\circ} =\frac{MH}{MN}=\frac{ \sqrt{3} }{ 2}\)
\(\tan30^{\circ} =\frac{NH}{MH}=\frac{ 1}{\sqrt{3}}; \cot30^{\circ} =\frac{MH}{NH}=\sqrt{3}\)
\(\sin60^{\circ} =\frac{MH}{MN}=\frac{ \sqrt{3} }{ 2}; \cos60^{\circ} =\frac{NH}{MN}=\frac{ 1}{ 2}\)
\(\tan60^{\circ} =\frac{MH}{NH}=\sqrt{3}; \cot60^{\circ} =\frac{NH}{MH}=\frac{ 1}{\sqrt{3}}\)
Thực hành 2 Trang 62 Toán 9 tập 1 Chân trời
Tính giá trị của các biểu thức sau:
a) \(A=\frac{2\cos 45^{\circ} }{\sqrt{2}}+\sqrt{3}\tan 30^{\circ}\)
b) \(B=\frac{2\sin 60^{\circ} }{\sqrt{3}}- \cot 45^{\circ}\)
Hướng dẫn giải:
a) \(A=\frac{2\cos 45^{\circ} }{\sqrt{2}}+\sqrt{3}\tan 30^{\circ}\)
\(A=\frac{2.\frac{\sqrt{2} }{ 2} }{\sqrt{2}}+\sqrt{3}.\frac{\sqrt{3} }{ 2}\)
\(A=1+ \frac{3 }{ 2} =\frac{5}{ 2}\)
b) \(B=\frac{2\sin 60^{\circ} }{\sqrt{3}}- \cot 45^{\circ}\)
\(B=\frac{2.\frac{\sqrt{3}}{ 2} }{\sqrt{3}}- 1\)
B = 1 − 1 = 0
Vận dụng 2 Trang 62 Toán 9 tập 1 Chân trời
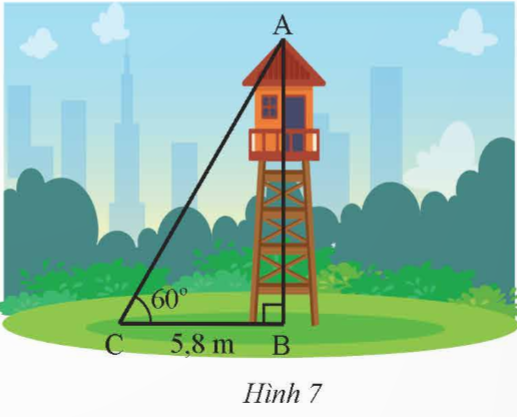
Tìm chiều cao của tháp canh trong Hình 7 (kết quả làm tròn đến hàng phần trăm).
Hướng dẫn giải:
Xét tam giác ABC vuông tại A, ta có:
\(\tan C=\frac{AB}{BC}\)
Suy ra AB = BC . tan C = 5,8 . tan 60o ≈ 10,05 m.
Vậy chiều cao của tháp canh khoảng 10,05 m.
----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 63 tập 1 Chân trời sáng tạo
Lời giải Toán 9 trang 62 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 1: Tỉ số lượng giác của góc nhọn , được VnDoc biên soạn và đăng tải!
