Giải Toán 9 trang 107 tập 1 Kết nối tri thức
Giải Toán 9 trang 107 Tập 1
Giải Toán 9 trang 107 tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 1 trang 107.
Bài 5.24 Trang 107 Toán 9 Tập 1
Hình 5.37 cho thấy hình ảnh của những đường tròn (là viền ngoài của các sản phẩm) qua cách trình bày một số sản phẩm mây tre đan. Bằng cách đánh số các đường tròn, em hãy chỉ ra một vài cặp đường tròn cắt nhau và cặp đường tròn không giao nhau.
Hướng dẫn giải:
− Một vài cặp đường tròn cắt nhau là: 2 và 3; 4 và 5; 7 và 8
− Một vài cặp đường tròn không giao nhau: 1 và 2; 2 và 5; 7 và 9;...
Bài 5.25 Trang 107 Toán 9 Tập 1
Cho hai điểm O và O' cách nhau một khoảng 5 cm. Mỗi đường tròn sau đây có vị trí tương đối như thế nào đối với đường tròn (O; 3 cm).
a) Đường tròn (O'; 3 cm)
b) Đường tròn (O'; 1 cm)
c) Đường tròn (O'; 8 cm)
Hướng dẫn giải:
Ta có: R = 3; OO' = 5 cm
a) Với r' = 3 cm, ta có: R - r < OO' < R + r nên (O; 3 cm) và (O'; 3 cm) cắt nhau
b) Với r' = 1, ta có: OO' > R + r nên (O; 3 cm) và (O'; 1 cm) nằm ngoài nhau.
c) Với r' = 8, ta có: OO' = r - R nên (O; 3 cm) và (O'; 8 cm) tiếp xúc trong.
Bài 5.26 Trang 107 Toán 9 Tập 1
Cho ba điểm thẳng hàng O, A và O'. Với mỗi trường hợp sau, hãy viết hệ thức giữa các độ dài OO', OA và O'A rồi xét xem hai đường tròn (O; OA) và (O'; O'A) tiếp xúc trong hay tiếp xúc ngoài với nhau; vẽ hình để khẳng định dự đoán của mình.
a) Điểm A nằm giữa hai điểm O và O'
b) Điểm O nằm giữa hai điểm A và O'
c) Điểm O' nằm giữa hai điểm A và O
Hướng dẫn giải:
a) Ta có hệ thức: OO' = OA + O'A
Do đó (O; OA) và (O'; O'A) tiếp xúc ngoài tại A
b) Ta có hệ thức: OO' = O'A – OA
Do đó (O; OA) và (O'; O'A) tiếp xúc trong tại A, (O') đựng (O)
c) Ta có hệ thức: OO' = OA – O'A
Do đó (O; OA) và (O'; O'A) tiếp xúc trong tại A, (O) đựng (O')
Bài 5.27 Trang 107 Toán 9 Tập 1
Cho hai đường tròn (O) và (O') tiếp xúc ngoài với nhau tại A. Một đường thẳng qua A cắt (O) tại B và cắt (O') tại C. Chứng minh rằng OB // O'C.
Hướng dẫn giải:
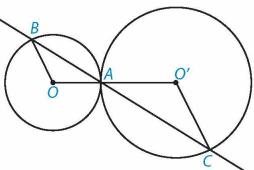
Vì (O) và (O') tiếp xúc ngoài tại A nên A nằm giữa O và O'
Do đó 
\(\widehat{OAB}=\widehat{O'AC}\) (hai góc đối đỉnh)
Mặt khác:
Δ OAB cân tại O nên \(\widehat{OAB}=\widehat{OBA}\)
Δ O'AC cân tại O' nên \(\widehat{O'CA}=\widehat{O'AC}\)
Suy ra \(\widehat{OBA}=\widehat{O'CA}\)
Mà hai góc này ở vị trí so le trong
Do đó OB // O'C
-----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 109 tập 1 Kết nối tri thức
Lời giải Toán 9 trang 107 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 17: Vị trí tương đối của hai đường tròn, được VnDoc biên soạn và đăng tải!
