Toán 9 Kết nối tri thức Bài 4: Phương trình quy về phương trình bậc nhất một ẩn

Giải Toán 9 Kết nối tri thức Bài 4: Phương trình quy về phương trình bậc nhất một ẩn hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong Toán 9 Kết nối tri thức tập 1 trang 27, 28, 29, 30. Mời các bạn tham khảo.

Phương trình quy về phương trình bậc nhất một ẩn

Mở đầu trang 26 Toán 9 Tập 1:
Giải Toán 9 trang 27
Giải Toán 9 trang 28
Giải Toán 9 trang 29
Giải Toán 9 trang 30

Mở đầu trang 26 Toán 9 Tập 1:

Trong một khu vườn hình vuông có cạnh bằng 15 m người ta làm một lối đi xung quanh vườn có bề rộng là x (m) (H.2.1). Để diện tích phần đất còn lại là 169 m² thì bề rộng x của lối đi là bao nhiêu?

Mở đầu trang 26 Toán 9 Tập 2 | Kết nối tri thức Giải Toán 9

Hướng dẫn giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

Do lối đi có bề rộng là x nên cạnh của khu vườn hình vuông ban đầu giảm đi $2x\left( m \right).$ $2x\left( m \right).$

Nên phần đất còn lại là hình vuông có cạnh $15 - 2x\left( m \right)$ $15 - 2x\left( m \right)$

Diện tích phần đất còn lại là $169{m^2}$ $169{m^2}$ nên ta có phương trình ${\left( {15 - 2x} \right)^2} = 169$ ${\left( {15 - 2x} \right)^2} = 169$

$\begin{array}{l}{\left( {15 - 2x} \right)^2} = {13^2}\\TH1:15 - 2x = 13\\2x = 2\\x = 1\end{array}$ $\begin{array}{l}{\left( {15 - 2x} \right)^2} = {13^2}\\TH1:15 - 2x = 13\\2x = 2\\x = 1\end{array}$

$TH2:15 - 2x = - 13$ (vô lý vì cạnh của mảnh đất >0)

Vậy $x = 1$

Vậy bề rộng của lối đi là 1m.

Giải Toán 9 trang 27

Hoạt động 1 trang 27 Toán 9 Kết nối tri thức

Phân tích đa thức $P\left( x \right) = \left( {x + 1} \right)\left( {2x - 1} \right) + \left( {x + 1} \right)x$ $P\left( x \right) = \left( {x + 1} \right)\left( {2x - 1} \right) + \left( {x + 1} \right)x$ thành nhân tử

Hướng dẫn giải:

$P\left( x \right) = \left( {x + 1} \right)\left( {2x - 1} \right) + \left( {x + 1} \right)x$ $P\left( x \right) = \left( {x + 1} \right)\left( {2x - 1} \right) + \left( {x + 1} \right)x$

$= \left( {x + 1} \right)\left( {2x - 1 + x} \right)$ $= \left( {x + 1} \right)\left( {2x - 1 + x} \right)$

$= \left( {x + 1} \right)\left( {3x - 1} \right)$ $= \left( {x + 1} \right)\left( {3x - 1} \right)$

Hoạt động 2 trang 27 Toán 9 Kết nối tri thức

Giải phương trình $P\left( x \right) = 0.$ $P\left( x \right) = 0.$ $B\left( x \right) = 0$ $B\left( x \right) = 0$

Hướng dẫn giải:

$\begin{array}{l}P\left( x \right) = 0\\\left( {x + 1} \right)\left( {3x - 1} \right) = 0\\TH1:x + 1 = 0\\x = - 1\\TH2:3x - 1 = 0\\x = \frac{1}{3}\end{array}$ $\begin{array}{l}P\left( x \right) = 0\\\left( {x + 1} \right)\left( {3x - 1} \right) = 0\\TH1:x + 1 = 0\\x = - 1\\TH2:3x - 1 = 0\\x = \frac{1}{3}\end{array}$

Vậy $x \in \left\{ { - 1;\frac{1}{3}} \right\}$ $x \in \left\{ { - 1;\frac{1}{3}} \right\}$

Giải Toán 9 trang 28

Luyện tập 1 trang 28 Toán 9 Kết nối tri thức

Giải các phương trình sau:

a) $\left( {3x + 1} \right)\left( {2 - 4x} \right) = 0;$ $\left( {3x + 1} \right)\left( {2 - 4x} \right) = 0;$

b) ${x^2} - 3x = 2x - 6.$ ${x^2} - 3x = 2x - 6.$ $B\left( x \right) = 0$ $B\left( x \right) = 0$

Hướng dẫn giải:

a) $\left( {3x + 1} \right)\left( {2 - 4x} \right) = 0;$ $\left( {3x + 1} \right)\left( {2 - 4x} \right) = 0;$

$\begin{array}{l}TH1:3x + 1 = 0\\x = \frac{{ - 1}}{3}\\TH2:2 - 4x = 0\\x = \frac{1}{2}\end{array}$ $\begin{array}{l}TH1:3x + 1 = 0\\x = \frac{{ - 1}}{3}\\TH2:2 - 4x = 0\\x = \frac{1}{2}\end{array}$

Vậy $x \in \left\{ { - \frac{1}{3};\frac{1}{2}} \right\}$ $x \in \left\{ { - \frac{1}{3};\frac{1}{2}} \right\}$

b) ${x^2} - 3x = 2x - 6.$ ${x^2} - 3x = 2x - 6.$

$\begin{array}{l}{x^2} - 3x = 2x + 6\\x\left( {x - 3} \right) = 2\left( {x + 3} \right)\\x\left( {x - 3} \right) - 2\left( {x + 3} \right) = 0\\\left( {x - 2} \right) - \left( {x - 3} \right) = 0\\TH1:x - 2 = 0\\x = 2\\TH2:x - 3 = 0\\x = 3\end{array}$ $\begin{array}{l}{x^2} - 3x = 2x + 6\\x\left( {x - 3} \right) = 2\left( {x + 3} \right)\\x\left( {x - 3} \right) - 2\left( {x + 3} \right) = 0\\\left( {x - 2} \right) - \left( {x - 3} \right) = 0\\TH1:x - 2 = 0\\x = 2\\TH2:x - 3 = 0\\x = 3\end{array}$

Vậy $x \in \left\{ {2;3} \right\}$ $x \in \left\{ {2;3} \right\}$

Vận dụng trang 28 Toán 9 Kết nối tri thức

Giải bài toán ở tình huống mở đầu.

Tình huống mở đầu: Trong một khu vườn hình vuông có cạnh bằng 15m người ta làm một lối đi xung quanh vườn có bề rộng là x (m) (H.2.1). Để diện tích phần đất còn lại là $169{m^2}$ $169{m^2}$ thì bề rộng x của lối đi là bao nhiêu?

Mở đầu trang 26 Toán 9 Tập 2 | Kết nối tri thức Giải Toán 9

Hướng dẫn giải:

Do lối đi có bề rộng là x nên cạnh của khu vườn hình vuông ban đầu giảm đi $2x\left( m \right).$ $2x\left( m \right).$

Nên phần đất còn lại là hình vuông có cạnh $15 - 2x\left( m \right)$ $15 - 2x\left( m \right)$

Diện tích phần đất còn lại là $169{m^2}$ $169{m^2}$ nên ta có phương trình ${\left( {15 - 2x} \right)^2} = 169$ ${\left( {15 - 2x} \right)^2} = 169$

$\begin{array}{l}{\left( {15 - 2x} \right)^2} = {13^2}\\TH1:15 - 2x = 13\\2x = 2\\x = 1\end{array}$ $\begin{array}{l}{\left( {15 - 2x} \right)^2} = {13^2}\\TH1:15 - 2x = 13\\2x = 2\\x = 1\end{array}$

$TH2:15 - 2x = - 13$ (vô lý vì cạnh của mảnh đất >0)

Vậy $x = 1$

Vậy bề rộng của lối đi là 1m.

Hoạt động 3 trang 28 Toán 9 Kết nối tri thức

Xét phương trình $x + \frac{1}{{x + 1}} = - 1 + \frac{1}{{x + 1}}.$ $x + \frac{1}{{x + 1}} = - 1 + \frac{1}{{x + 1}}.$

Chuyển các biểu thức chứa ẩn từ vế phải sang vế trái, rồi thu gọn vế trái.

Hướng dẫn giải:

Ta có $x + \frac{1}{{x + 1}} = - 1 + \frac{1}{{x + 1}}$ $x + \frac{1}{{x + 1}} = - 1 + \frac{1}{{x + 1}}$ hay $x + \frac{1}{{x + 1}} + 1 - \frac{1}{{x + 1}} = 0$ $x + \frac{1}{{x + 1}} + 1 - \frac{1}{{x + 1}} = 0$ suy ra $x + 1 = 0$

Hoạt động 4 trang 28 Toán 9 Kết nối tri thức

Xét phương trình $x + \frac{1}{{x + 1}} = - 1 + \frac{1}{{x + 1}}.$ $x + \frac{1}{{x + 1}} = - 1 + \frac{1}{{x + 1}}.$

Giá trị $x = - 1$ có là nghiệm của phương trình đã cho hay không? Vì sao?

Hướng dẫn giải:

Thay $x = - 1$ vào phương trình đã cho ta có $\left( { - 1} \right) + \frac{1}{{ - 1 + 1}} = - 1 + \frac{1}{{ - 1 + 1}}$ $\left( { - 1} \right) + \frac{1}{{ - 1 + 1}} = - 1 + \frac{1}{{ - 1 + 1}}$, ta có kết quả đã cho chưa đúng vì khi thay $x = - 1$ làm cho mẫu của phân số bằng 0.

Vậy $x = - 1$ không là nghiệm của phương trình.

Luyện tập 2 trang 28 Toán 9 Kết nối tri thức

Tìm điều kiện xác định của mỗi phương trình sau:

a) $\frac{{3x + 1}}{{2x - 1}} = 1;$ $\frac{{3x + 1}}{{2x - 1}} = 1;$

b) $\frac{x}{{x - 1}} + \frac{{x + 1}}{x} = 2.$ $\frac{x}{{x - 1}} + \frac{{x + 1}}{x} = 2.$

Hướng dẫn giải:

a) $\frac{{3x + 1}}{{2x - 1}} = 1;$ $\frac{{3x + 1}}{{2x - 1}} = 1;$

Vì $2x - 1 \ne 0$ $2x - 1 \ne 0$ khi $x \ne \frac{1}{2}.$ $x \ne \frac{1}{2}.$ Vậy ĐKXĐ của phương trình đã cho là $x \ne \frac{1}{2}.$ $x \ne \frac{1}{2}.$

b) $\frac{x}{{x - 1}} + \frac{{x + 1}}{x} = 2.$ $\frac{x}{{x - 1}} + \frac{{x + 1}}{x} = 2.$

Vì $x - 1 \ne 0$ $x - 1 \ne 0$ khi $x \ne 1$ $x \ne 1$ và $x \ne 0$ $x \ne 0$. Vậy ĐKXĐ của phương trình đã cho là $x \ne 1$ $x \ne 1$ và $x \ne 0$ $x \ne 0$.

Giải Toán 9 trang 29

Hoạt động 5 trang 29 Toán 9 Kết nối tri thức

Xét phương trình $\frac{{x + 3}}{x} = \frac{{x + 9}}{{x - 3}}.\left( 2 \right)$ $\frac{{x + 3}}{x} = \frac{{x + 9}}{{x - 3}}.\left( 2 \right)$

Hãy thực hiện các yêu cầu sau để giải phương trình (2):

a) Tìm điều kiện xác định của phương trình (2);

b) Quy đồng mẫu hai vế của phương trình (2), rồi khử mẫu;

c) Giải phương trình vừa tìm được;

d) Kết luận nghiệm của phương trình (2).

Hướng dẫn giải:

a) ĐKXĐ $x \ne 0$ $x \ne 0$ và $x \ne 3.$ $x \ne 3.$

b) Quy đồng mẫu ta được $\frac{{\left( {x + 3} \right)\left( {x - 3} \right)}}{{x\left( {x - 3} \right)}} = \frac{{\left( {x + 9} \right)x}}{{x\left( {x - 3} \right)}}$ $\frac{{\left( {x + 3} \right)\left( {x - 3} \right)}}{{x\left( {x - 3} \right)}} = \frac{{\left( {x + 9} \right)x}}{{x\left( {x - 3} \right)}}$ và khử mẫu ta có: $\left( {x - 3} \right)\left( {x + 3} \right) = x\left( {x + 9} \right)$ $\left( {x - 3} \right)\left( {x + 3} \right) = x\left( {x + 9} \right)$

c) ${x^2} - 9 = {x^2} + 9x$ ${x^2} - 9 = {x^2} + 9x$

$\begin{array}{l}{x^2} - {x^2} - 9x = 9\\ - 9x = 9\\x = - 1\end{array}$ $\begin{array}{l}{x^2} - {x^2} - 9x = 9\\ - 9x = 9\\x = - 1\end{array}$

Giá trị $x = - 1\left( {t/m} \right)$ $x = - 1\left( {t/m} \right)$. Vậy nghiệm của phương trình là $x = - 1.$

Luyện tập 3 trang 29 Toán 9 Kết nối tri thức

Giải phương trình $\frac{1}{{x - 1}} - \frac{{4x}}{{{x^3} - 1}} = \frac{x}{{{x^2} + x + 1}}.$ $\frac{1}{{x - 1}} - \frac{{4x}}{{{x^3} - 1}} = \frac{x}{{{x^2} + x + 1}}.$

Hướng dẫn giải:

ĐKXĐ: $x \ne 1.$ $x \ne 1.$

Quy đồng mẫu thức, ta được

$\frac{{1.\left( {{x^2} + x + 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} - \frac{{4x}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} = \frac{{x\left( {x - 1} \right)}}{{\left( {{x^2} + x + 1} \right)\left( {x - 1} \right)}}$ $\frac{{1.\left( {{x^2} + x + 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} - \frac{{4x}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} = \frac{{x\left( {x - 1} \right)}}{{\left( {{x^2} + x + 1} \right)\left( {x - 1} \right)}}$

Khử mẫu ta được ${x^2} + x + 1 - 4x = x\left( {x - 1} \right)$ ${x^2} + x + 1 - 4x = x\left( {x - 1} \right)$

$\begin{array}{l}{x^2} + x + 1 - 4x = {x^2} - x\\{x^2} - 3x - {x^2} + x = - 1\\ - 2x = - 1\end{array}$ $\begin{array}{l}{x^2} + x + 1 - 4x = {x^2} - x\\{x^2} - 3x - {x^2} + x = - 1\\ - 2x = - 1\end{array}$

$x = \frac{1}{2}\left( {t/m} \right).$ $x = \frac{1}{2}\left( {t/m} \right).$

Vậy nghiệm của phương trình là $x = \frac{1}{2}.$ $x = \frac{1}{2}.$

Giải Toán 9 trang 30

Bài 2.1 trang 30 Toán 9 Tập 1:

Giải các phương trình sau:

a) x(x – 2) = 0;

b) (2x + 1)(3x – 2) = 0.

Hướng dẫn giải

a) x(x – 2) = 0

Suy ra x = 0 hoặc x – 2 = 0

Do đó x = 0 hoặc x = 2.

Vậy phương trình đã cho có nghiệm x = 0 và x = 2.

b) (2x + 1)(3x – 2) = 0

Ta giải hai phương trình sau:

⦁ 2x + 1 = 0 hay 2x = –1, suy ra x= $-\frac{1}{2}$ $-\frac{1}{2}$

⦁ 3x – 2 = 0 hay 3x = 2, suy ra x= $\frac{2}{3}$ $\frac{2}{3}$

Vậy phương trình đã cho có nghiệm x= $-\frac{1}{2}$ $-\frac{1}{2}$ và x= $\frac{2}{3}$ $\frac{2}{3}$

Bài 2.2 trang 30 Toán 9 Tập 1:

Giải các phương trình sau:

a) (x² – 4) + x(x – 2) = 0;

b) (2x + 1) ² – 9x ² = 0.

Hướng dẫn giải

a) (x² – 4) + x(x – 2) = 0

(x – 2)(x + 2) + x(x – 2) = 0

(x – 2)(x + 2 + x) = 0

(x – 2)(2x + 2) = 0.

Ta giải hai phương trình sau:

⦁ x – 2 = 0, suy ra x = 2.

⦁ 2x + 2 = 0 hay 2x = –2, suy ra x = –1.

Vậy phương trình đã cho có nghiệm là x = 2 và x = –1.

b) (2x + 1) ² – 9x ² = 0

(2x + 1)² – (3x)² = 0

(2x + 1 – 3x)(2x + 1 + 3x) = 0

(–x + 1)(5x + 1) = 0.

Ta giải hai phương trình sau:

⦁ –x + 1 = 0, suy ra x = 1.

⦁ 5x + 1 = 0 hay 5x = –1, suy ra x= $-\frac{1}{5}$ $-\frac{1}{5}$

Vậy phương trình đã cho có nghiệm là x = 1 và x= $-\frac{1}{5}$ $-\frac{1}{5}$

Bài 2.3 trang 30 Toán 9 Tập 1:

Giải các phương trình sau:

a) $\frac{2}{{2x + 1}} + \frac{1}{{x + 1}} = \frac{3}{{\left( {2x + 1} \right)\left( {x + 1} \right)}};$ $\frac{2}{{2x + 1}} + \frac{1}{{x + 1}} = \frac{3}{{\left( {2x + 1} \right)\left( {x + 1} \right)}};$

b) $\frac{1}{{x + 1}} - \frac{x}{{{x^2} - x + 1}} = \frac{{3x}}{{{x^3} + 1}}.$ $\frac{1}{{x + 1}} - \frac{x}{{{x^2} - x + 1}} = \frac{{3x}}{{{x^3} + 1}}.$

Hướng dẫn giải

a) $\frac{2}{{2x + 1}} + \frac{1}{{x + 1}} = \frac{3}{{\left( {2x + 1} \right)\left( {x + 1} \right)}};$ $\frac{2}{{2x + 1}} + \frac{1}{{x + 1}} = \frac{3}{{\left( {2x + 1} \right)\left( {x + 1} \right)}};$

ĐKXĐ: $x \ne - 1;x \ne \frac{{ - 1}}{2}.$ $x \ne - 1;x \ne \frac{{ - 1}}{2}.$

Quy đồng mẫu thức ta được:

$\frac{{2\left( {x + 1} \right)}}{{\left( {2x + 1} \right)\left( {x + 1} \right)}} + \frac{{1.\left( {2x + 1} \right)}}{{\left( {x + 1} \right)\left( {2x + 1} \right)}} = \frac{3}{{\left( {2x + 1} \right)\left( {x + 1} \right)}};$ $\frac{{2\left( {x + 1} \right)}}{{\left( {2x + 1} \right)\left( {x + 1} \right)}} + \frac{{1.\left( {2x + 1} \right)}}{{\left( {x + 1} \right)\left( {2x + 1} \right)}} = \frac{3}{{\left( {2x + 1} \right)\left( {x + 1} \right)}};$

Khử mẫu ta được:

$\begin{array}{l}2\left( {x + 1} \right) + 1.\left( {2x + 1} \right) = 3\\4x + 3 = 3\\x = 0\left( {t/m} \right).\end{array}$ $\begin{array}{l}2\left( {x + 1} \right) + 1.\left( {2x + 1} \right) = 3\\4x + 3 = 3\\x = 0\left( {t/m} \right).\end{array}$

Vậy nghiệm của phương trình đã cho là $x = 0.$

b) $\frac{1}{{x + 1}} - \frac{x}{{{x^2} - x + 1}} = \frac{{3x}}{{{x^3} + 1}}.$ $\frac{1}{{x + 1}} - \frac{x}{{{x^2} - x + 1}} = \frac{{3x}}{{{x^3} + 1}}.$

ĐKXĐ: $x \ne - 1;x \ne \frac{{ - 1}}{2}.$ $x \ne - 1;x \ne \frac{{ - 1}}{2}.$

Quy đồng mẫu thức ta được: $\frac{{1.\left( {{x^2} - x + 1} \right)}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} - \frac{{x\left( {x + 1} \right)}}{{\left( {{x^2} - x + 1} \right)\left( {x + 1} \right)}} = \frac{{3x}}{{\left( {{x^2} - x + 1} \right)\left( {x + 1} \right)}}.$ $\frac{{1.\left( {{x^2} - x + 1} \right)}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} - \frac{{x\left( {x + 1} \right)}}{{\left( {{x^2} - x + 1} \right)\left( {x + 1} \right)}} = \frac{{3x}}{{\left( {{x^2} - x + 1} \right)\left( {x + 1} \right)}}.$

Khử mẫu ta được:

$\begin{array}{l}1.\left( {{x^2} - x + 1} \right) - x\left( {x + 1} \right) = 3x\\ - 2x + 1 = 3x\\5x = 1\\x = \frac{1}{5}\left( {t/m} \right).\end{array}$ $\begin{array}{l}1.\left( {{x^2} - x + 1} \right) - x\left( {x + 1} \right) = 3x\\ - 2x + 1 = 3x\\5x = 1\\x = \frac{1}{5}\left( {t/m} \right).\end{array}$

Vậy nghiệm của phương trình đã cho là $x = \frac{1}{5}.$ $x = \frac{1}{5}.$

Bài 2.4 trang 30 Toán 9 Tập 1:

Bác An có một mảnh đất hình chữ nhật với chiều dài 14 m và chiều rộng 12 m. Bác dự định xây nhà trên mảnh đất đó và dành một phần diện tích đất để làm sân vườn như Hình 2.2. Biết diện tích đất làm nhà là 100 m2. Hỏi x bằng bao nhiêu mét?

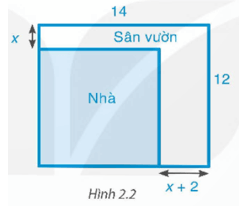
Bài 2.4 trang 30 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Hướng dẫn giải

Chiều dài của phần đất làm nhà là: 14 – (x + 2) = 12 – x (m). Điều kiện x < 12.

Chiều rộng của phần đất làm nhà là: 12 – x (m).

Diện tích đất làm nhà là: (12 – x)² (m²).

Theo bài, diện tích đất làm nhà là 100 m ² nên ta có phương trình:

(12 – x)² = 100. (*)

Giải phương trình (*):

(12 – x)² = 100

(12 – x)² – 10² = 0

(12 – x – 10)(12 – x + 10) = 0

(2 – x)(22 – x) = 0

Suy ra 2 – x = 0 hoặc 22 – x = 0

Do đó x = 2 hoặc x = 22.

Ta thấy x = 2 thỏa mãn điều kiện x < 12.

Vậy x = 2.

Bài 2.5 trang 30 Toán 9 Tập 1:

Hai người cùng làm chung một công việc thì xong trong 8 giờ. Hai người cùng làm được 4 giờ thì người thứ nhất bị điều đi làm công việc khác. Người thứ hai tiếp tục làm việc trong 12 giờ nữa thì xong công việc. Gọi x là thời gian người thứ nhất làm một mình xong công việc (đơn vị tính là giờ, $x > 0$).

a) Hãy biểu thị theo x:

- Khối lượng công việc mà người thứ nhất làm được trong 1 giờ;

- Khối lượng công việc mà người thứ hai làm được trong 1 giờ;

b) Hãy lập phương trình theo x và giải phương trình đó. Sau đó cho biết, nếu làm một mình thì mỗi người phải làm trong bao lâu mới xong công việc đó.

Hướng dẫn giải

a)

- Một giờ người thứ nhất làm được số công việc là $\frac{1}{x}$ $\frac{1}{x}$ (công việc)

- Hai người làm công việc 8 giờ thì xong nên một giờ hai người làm được số công việc là $\frac{1}{8}$ $\frac{1}{8}$ (công việc)

Nên một giờ người thứ hai làm được $\frac{1}{8} - \frac{1}{x}$ $\frac{1}{8} - \frac{1}{x}$ (công việc)

b) Hai người cùng làm trong 4 giờ thì làm được $4.\frac{1}{8} = \frac{1}{2}$ $4.\frac{1}{8} = \frac{1}{2}$ (công việc)

Người thứ hai làm tiếp tục một mình trong 12h làm được $12.\left( {\frac{1}{8} - \frac{1}{x}} \right) = \frac{3}{2} - \frac{{12}}{x}$ $12.\left( {\frac{1}{8} - \frac{1}{x}} \right) = \frac{3}{2} - \frac{{12}}{x}$ (công việc) thì xong công việc nên ta có phương trình:

$\frac{1}{2} + \left( {\frac{3}{2} - \frac{{12}}{x}} \right) = 1$ $\frac{1}{2} + \left( {\frac{3}{2} - \frac{{12}}{x}} \right) = 1$ hay $\frac{3}{2} - \frac{{12}}{x} = \frac{1}{2}$ $\frac{3}{2} - \frac{{12}}{x} = \frac{1}{2}$ suy ra $\frac{{12}}{x} = 1$ $\frac{{12}}{x} = 1$ nên $x = 12\left( {t/m} \right)$ $x = 12\left( {t/m} \right)$

Với $x = 12$ thì một giờ người thứ hai làm được $\frac{1}{8} - \frac{1}{{12}} = \frac{1}{{24}}$ $\frac{1}{8} - \frac{1}{{12}} = \frac{1}{{24}}$ (công việc)

Do đó thời gian hoàn thành công việc của người thứ hai nếu làm một mình là $1:\frac{1}{{24}} = 24$ $1:\frac{1}{{24}} = 24$ (giờ)

Vậy nếu làm riêng người thứ nhất hoàn thành công việc trong 12 h.

Người thứ hai hoàn thành công việc trong 24 h.

Câu hỏi trong bài

Chia sẻ, đánh giá bài viết

1

235

Bài trước

Bài sau