Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
VnDoc.com Lớp 9 Toán 9 Kết nối tri thức

Giải Toán 9 trang 67 tập 1 Kết nối tri thức

Giải Toán 9 trang 67 Tập 1

Giải Toán 9 trang 67 tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 1 trang 67.

Câu hỏi Trang 67 Toán 9 Tập 1

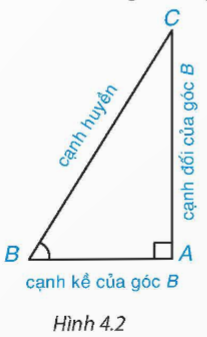
Xét góc C của tam giác ABC vuông tại A (H.4.3). Hãy chỉ ra cạnh đối và cạnh kề của góc C.

Hướng dẫn giải:

Cạnh đối của góc C là cạnh AB

Cạnh kề của góc C là cạnh AC

Hoạt động 1 Trang 67 Toán 9 Tập 1

Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \widehat B = \widehat {B'} = \alpha . Chứng minh rằng:

a) \Delta ABC\backsim \Delta A'B'C'

b) \frac{{AC}}{{BC}} = \frac{{A'C'}}{{B'C'}};\ \frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}};\ \frac{{AC}}{{AB}} = \frac{{A'C'}}{{A'B'}};\ \frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}

Hướng dẫn giải:

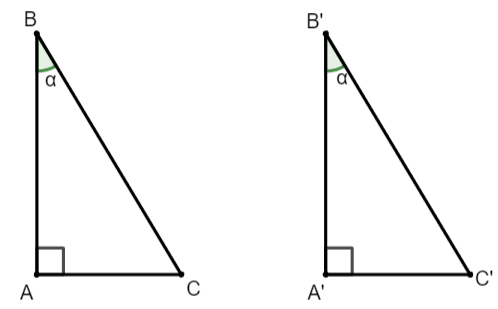
a) Xét tam giác ABC và tam giác A’B’C’ ta có:

\widehat A = \widehat {A'} = {90^0}

\widehat B = \widehat {B'} = \alpha

Do đó \Delta ABC\backsim \Delta A'B'C'\left( g-g \right)

b) Ta có \Delta ABC\backsim \Delta A'B'C' (cma)

Suy ra \frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}

Từ đó suy ra các tỉ lệ thức: \frac{{AC}}{{BC}} = \frac{{A'C'}}{{B'C'}};\ \frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}};

\ \frac{{AC}}{{AB}} = \frac{{A'C'}}{{A'B'}};\ \frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}

-----------------------------------------------

---> Xem thêm: Giải Toán 9 trang 68 tập 1 Kết nối tri thức

Toán 9 Kết nối tri thức Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Lời giải Toán 9 trang 67 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 11: Tỉ số lượng giác của góc nhọn, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết
1
1 Bài viết đã được lưu
Mục lục
Tìm thêm: toán 9 giải toán 9 giải toán 9 kntt
Sắp xếp theo
Xóa Đăng nhập để Gửi
    Toán lớp 9 Sách mới

    Tham khảo thêm

    Toán 9 Kết nối tri thức

    Xem thêm