VnDoc.com

Toán 9 Kết nối tri thức Bài 18: Hàm số y = ax^2 (a khác 0)

Giải Toán 9 KNTT tập 2

Bài trước

Tải về

Bài sau

Bài 18: Hàm số y = ax² (a khác 0)

Giải Toán 9 Kết nối tri thức Bài 18: Hàm số y = ax² (a khác 0) hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 2 trang 5, 6, 7, 8, giúp các em nắm vững kiến thức và luyện giải môn Toán lớp 9. Mời các bạn tham khảo.

Mở đầu trang 4 Toán 9 Tập 2

Một cây cầu treo có trụ tháp đôi cao 75 m so với mặt của cây cầu và cách nhau 400 m. Các dây cáp có dạng đồ thị của hàm số y = ax² (a ≠ 0) như Hình 6.1 và được treo trên các đỉnh tháp. Tìm chiều cao CH của dây cáp biết điểm H cách tâm O của cây cầu 100 m (giả sử mặt của cây cầu là bằng phẳng).

Hướng dẫn giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

Vì các dây cáp có dạng đồ thị của hàm số y = ax² (a ≠ 0) được treo trên các đỉnh tháp nên đồ thị hàm số y = ax² (a ≠ 0) đi qua điểm B(200; 75).

Thay x = 200 và y = 75 vào hàm số y = ax², ta được:

75 = a . 200², hay 40 000a = 75, suy ra a = 0,001875 (thỏa mãn a ≠ 0).

Khi đó ta có hàm số y = 0,001875x².

Chiều cao CH của dây cáp chính là tung độ của điểm C thuộc đồ thị hàm số y = 0,001875x².

Thay hoành độ điểm C là x = 100 vào hàm số y = 0,001875x², ta được:

y = 0,001875 . 100² = 18,75.

Vậy chiều cao CH của dây cáp là 18,75 mét.

1. Hàm số y = ax² (a≠0)

HĐ1 trang 5 Toán 9 Tập 2: Khi thả một vật rơi tự do và bỏ qua sức cản của không khí, quãng đường chuyển động s (mét) của vật được cho bằng công thức s = 4,9t², trong đó t là thời gian chuyển động của vật (giây).

a) Hoàn thành bảng sau vào vở:

b) Giả sử một vật rơi tự do từ độ cao 19,6 m so với mặt đất. Hỏi sau bao lâu vật chạm đất?

Hướng dẫn giải:

a) Thay t = 0 vào công thức s = 4,9t², ta được: s = 4,9 . 0² = 0.

Thay t = 1 vào công thức s = 4,9t², ta được: s = 4,9 . 1² = 4,9.

Thay t = 2 vào công thức s = 4,9t², ta được: s = 4,9 . 2² = 19,6.

Ta hoàn thành được bảng như sau:

t (giây)	0	1	2
s (m)	0	4,9	19,6

b) Vật rơi tự do từ độ cao 19,6 mét so với mặt đất tức là quãng đường chuyển động của vật là s = 19,6 (m).

Từ bảng kết quả câu a, ta thấy khi t = 2 (giây) thì s = 19,6 (mét).

Vậy nếu một vật rơi tự do từ độ cao 19,6 m so với mặt đất thì sau 2 giây vật sẽ chạm đất.

HĐ2 trang 5 Toán 9 Tập 2 :

a) Viết công thức tính diện tích S của hình tròn bán kính r.

b) Hoàn thành bảng sau vào vở (lấy π = 3,14 và làm tròn kết quả đến chữ số thập phân thứ hai):

Hướng dẫn giải:

a) Công thức tính diện tích S của hình tròn bán kính r là:

S = πr² (đơn vị diện tích).

b) Thay r = 1 và π = 3,14 vào công thức S = πr², ta được: S = 3,14 . 1² = 3,14.

Thay r = 2 và π = 3,14 vào công thức S = πr², ta được: S = 3,14 . 2² = 12,56.

Thay r = 3 và π = 3,14 vào công thức S = πr², ta được: S = 3,14 . 3² = 28,26.

Thay r = 4 và π = 3,14 vào công thức S = πr², ta được: S = 3,14 . 4² = 50,24.

Ta hoàn thành được bảng như sau:

r (cm)	1	2	3	4
S (cm²)	3,14	12,56	28,26	50,24

2. Đồ thị của hàm số y = ax² (a≠0)

HĐ3 trang 6 Toán 9 Tập 2 : Cho hàm số y = 2x².

a) Hoàn thành bảng giá trị sau vào vở:

b) Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; 2x²) với x ∈ ℝ và nối lại, ta được đồ thị của hàm số y = 2x².

Hướng dẫn giải:

a) Thay lần lượt các giá trị x = –3; x = –2; …; x = 3 vào hàm số y = 2x², ta được bảng giá trị:

x	–3	–2	–1	0	1	2	3
y = 2x²	18	8	2	0	2	8	18

b) Biểu diễn các điểm (–3; 18); (–2; 8); (–1; 2); (0; 0); (1; 2); (2; 8) và (3; 18) trong bảng giá trị ở câu a và các điểm (x; 2x²) với x ∈ ℝ trên mặt phẳng tọa độ Oxy, sau đó nối lại, ta được đồ thị của hàm số y = 2x² như sau:

Vận dụng 2 trang 8 Toán 9 Tập 2 : Giải quyết bài toán ở tình huống mở đầu.

Hướng dẫn giải:

Vì các dây cáp có dạng đồ thị của hàm số y = ax² (a ≠ 0) được treo trên các đỉnh tháp nên đồ thị hàm số y = ax² (a ≠ 0) đi qua điểm B(200; 75).

Thay x = 200 và y = 75 vào hàm số y = ax², ta được:

75 = a . 200², hay 40 000a = 75, suy ra a = 0,001875 (thỏa mãn a ≠ 0).

Khi đó ta có hàm số y = 0,001875x².

Chiều cao CH của dây cáp chính là tung độ của điểm C thuộc đồ thị hàm số y = 0,001875x².

Thay hoành độ điểm C là x = 100 vào hàm số y = 0,001875x², ta được:

y = 0,001875 . 100² = 18,75.

Vậy chiều cao CH của dây cáp là 18,75 mét.

Bài 18.1 trang 8 Toán 9 Tập 2 : Cho hàm số y = 0,25x². Hoàn thành bảng giá trị sau vào vở:

Bài 6.1 trang 8 Toán 9 Kết nối tri thức Tập 2 | Giải Toán 9

Hướng dẫn giải:

Thay lần lượt các giá trị x = –3; x = –2; …; x = 3 vào hàm số y = 0,25x², ta được bảng giá trị:

x	–3	–2	–1	0	1	2	3
y	2,25	1	0,25	0	0,25	1	2,25

Bài 18.2 trang 8 Toán 9 Tập 2 : Cho hình lăng trụ đứng có đáy là hình vuông cạnh a (cm) và chiều cao 10 cm.

a) Viết công thức tính thể tích V của lăng trụ theo a và tính giá trị của V khi a = 2 cm.

b) Nếu độ dài cạnh đáy tăng lên hai lần thì thể tích của hình lăng trụ thay đổi thế nào?

Hướng dẫn giải:

a) Thể tích của hình lăng trụ đứng đó là: V = Bh = 10a² (cm³).

Vậy công thức tính thể tích V của lăng trụ là V = 10a² (cm³).

Khi a = 2 cm, thay vào công thức V = 10a², ta được:

V = 10 . 2² = 40 (cm³).

Vậy V = 40 cm³ khi a = 2 cm.

b) Nếu độ dài cạnh đáy tăng lên hai lần thì độ dài cạnh đáy lúc này là 2a (cm).

Thể tích của hình lăng trụ lúc này là:

V’ = B’.h = 10 . (2a)² = 40a² = 4V (cm³).

Vậy nếu độ dài cạnh đáy tăng lên hai lần thì thể tích của hình lăng trụ tăng lên 4 lần.

Bài 18.3 trang 8 Toán 9 Tập 2 : Diện tích toàn phần S (cm²) của hình lập phương, tức là tổng diện tích xung quanh và diện tích của hai mặt đáy là một hàm số của độ dài cạnh a (cm).

a) Viết công thức của hàm số này.

b) Sử dụng công thức nhận được ở câu a để tính độ dài cạnh của một hình lập phương có diện tích toàn phần là 54 cm².

Hướng dẫn giải:

a) Diện tích toàn phần của hình lập phương là:

S = 2 . a² + 4 . a² = 6a² (cm²).

Vậy công thức của hàm số cần tìm là: S = 6a² (cm²).

b) Ta có S = 54 cm², thay vào công thức S = 6a², ta được:

54 = 6a², hay a² = 9. Suy ra a = 3 (do a > 0).

Vậy một hình lập phương có diện tích toàn phần là 54 cm² thì có độ dài cạnh bằng 3 cm.

Bài 18.3 trang 8 Toán 9 Tập 2:

Diện tích toàn phần $S\left( {c{m^2}} \right)$ $S (c m^{2})$ của hình lập phương, tức là tổng diện tích xung quanh và diện tích đáy hai mặt của hai mặt đáy là một hàm số của độ dài cạnh a (cm).

a) Viết công thức của hàm số này.

b) Sử dụng công thức nhận được ở câu a để tính độ dài cạnh của một hình lập phương có diện tích toàn phần là $54c{m^2}$ $54 c m^{2}$ .

Hướng dẫn giải:

a) Diện tích toàn phần của hình lập phương cạnh a là: $S = 6{a^2}\left( {c{m^2}} \right)$ $S = 6 a^{2} (c m^{2})$ .

b) Với $S = 54c{m^2}$ $S = 54 c m^{2}$ thay vào công thức $S = 6{a^2}$ $S = 6 a^{2}$ ta có: $54 = 6.{a^2} \Rightarrow {a^2} = 9 \Rightarrow a = 3$ $54 = 6. a^{2} \Rightarrow a^{2} = 9 \Rightarrow a = 3$ (do $a > 0$ )

Vậy với một hình lập phương có diện tích toàn phần là $54c{m^2}$ $54 c m^{2}$ thì độ dài cạnh là 3cm.

Chú ý khi giải: Độ dài cạnh của hình lập phương luôn lớn hơn 0.

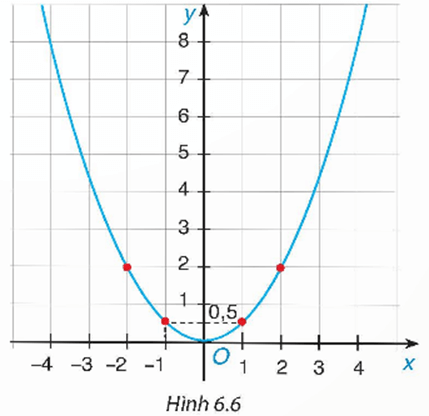
Bài 18.5 trang 8 Toán 9 Tập 2 : Biết rằng đường cong trong Hình 6.6 là một parabol y = ax².

a) Tìm hệ số a.

b) Tìm tung độ của điểm thuộc parabol có hoành độ x = –2.

c) Tìm các điểm thuộc parabol có tung độ y = 8.

Bài 6.5 trang 8 Toán 9 Kết nối tri thức Tập 2 | Giải Toán 9

Hướng dẫn giải:

a) Do parabol y = ax² trong Hình 6.6 đi qua điểm có tọa độ (2; 2) nên ta thay x = 2 và y = 2 vào hàm số y = ax² thì được:

2 = a . 2², hay 4a = 2. Suy ra a = $\frac{1}{2}$ $\frac{1}{2}$ .

b) Trên Hình 6.6, ta thấy parabol đi qua điểm có tọa độ (–2; 2).

Vậy điểm thuộc parabol có hoành độ x = –2 thì có tung độ là 2.

c) Với a = $\frac{1}{2}$ $\frac{1}{2}$ ta có hàm số $y=\frac{1}{2} x^{2}$ $y = \frac{1}{2} x^{2}$

Thay y = 8 vào hàm số trên, ta được: $8=\frac{1}{2} x^{2}$ $8 = \frac{1}{2} x^{2}$ , hay x² = 16.

Suy ra x = 4 hoặc x = –4.

Vậy các điểm thuộc parabol cần tìm là (–4; 8) và (4; 8).

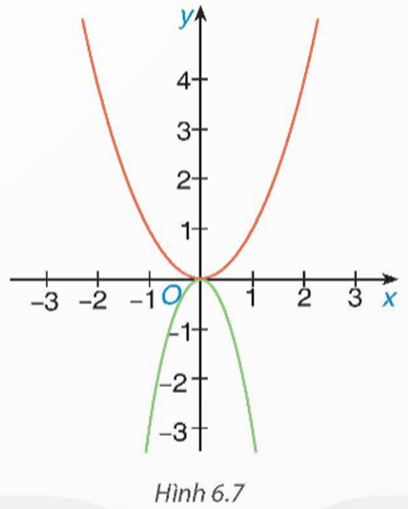
Bài 18.6 trang 9 Toán 9 Tập 2 : Trong Hình 6.7 có hai đường cong là đồ thị của hai hàm số y = –3x² và y = x². Hãy cho biết đường nào là đồ thị của hàm số y = –3x².

Bài 6.6 trang 9 Toán 9 Kết nối tri thức Tập 2 | Giải Toán 9

Hướng dẫn giải:

Đồ thị hàm số y = ax² (a ≠ 0) là đường cong parabol nằm phía trên trục hoành nếu a > 0 và nằm phía dưới trục hoành nếu a < 0.

Quan sát Hình 6,7, ta thấy đường cong màu đỏ nằm phía trên trục hoành và đường cong màu xanh nằm phía dưới trục hoành.

Mặt khác, hàm số y = –3x² có hệ số a = –3 < 0. Do vậy, đường cong màu xanh chính là đồ thị của hàm số y = –3x².

Chia sẻ, đánh giá bài viết

1

301

Bài trước

Bài sau

Chia sẻ bởi:
Đậu Phộng

Tải về

Chọn file muốn tải về:

Toán 9 Kết nối tri thức Bài 18: Hàm số y = ax^2 (a khác 0)

351,6 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!