Toán 9 Kết nối tri thức Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng
Giải Toán 9 Kết nối tri thức Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 1 trang 54, 55, 56, 57.
Giải Toán 9 KNTT bài 12
Bài 4.8 trang 78 Toán 9 Tập 1:
Giải tam giác ABC vuông tại A có BC = a,AC = b,AB = c, trong các trường hợp:
a) a = 21, b = 18;
b) b = 10,
\(\widehat C = {30^0};\)
c) c = 5, b = 3.
Hướng dẫn
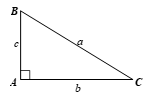
a) a = 21,b = 18;
Tam giác ABC vuông tại A, ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lý Pythagore)
Thay số ta có: \(A{B^2} + {18^2} = {21^2}\) hay \(AB = \sqrt {{{21}^2} - {{18}^2}} = 3\sqrt {13}\)(vì AB > 0)
Ta có \(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{{18}}{{21}} = \frac{6}{7}\)nên\(\widehat B \approx {59^0}\)
Mà \(\widehat B + \widehat C = {90^0}\) nên \(\widehat C = {90^0} - \widehat B \approx {90^0} - {59^0} = {31^0}\)
b) b = 10,\(\widehat C = {30^0};\)
Tam giác ABC vuông tại A, ta có \(\tan \widehat C = \frac{{AC}}{{AB}}\) hay \(\tan {30^0} = \frac{{10}}{{AB}}\) suy ra \(AB = \frac{{10}}{{\tan {{30}^0}}} = 10\sqrt 3\)
\(\sin \widehat C = \frac{{AC}}{{BC}}\) hay \(\sin {30^0} = \frac{{10}}{{BC}}\) suy ra \(BC = \frac{{10}}{{\sin {{30}^0}}} = 20\)
Mà \(\widehat B + \widehat C = {90^0} nên \widehat C = {90^0} - \widehat B = {90^0} - {30^0} = {60^0}\)
c) c = 5,b = 3.
Tam giác ABC vuông tại A, ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lý Pythagore)
Thay số ta có: \(B{C^2} = {5^2} + {3^2} = 34\) hay \(BC = \sqrt {34} (vì BC > 0)\)
Ta có \(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{3}{{\sqrt {34} }} nên \widehat B \approx {30^0}58'\)
Mà \(\widehat B + \widehat C = {90^0}\) nên \(\widehat C = {90^0} - \widehat B \approx {90^0} - {30^0}57' = {59^0}02'\)
Bài 4.9 trang 78 Toán 9 Tập 1:
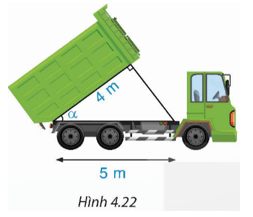
Hướng dẫn
Theo định nghĩa tỉ số lượng giác cos, ta có \(cosα=4/5\), từ đó tính được α ≈ 36°52’.
Vậy góc nghiêng α của thùng xe chở rác khoảng 36°52’.
Bài 4.10 trang 78 Toán 9 Tập 1:
Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23.
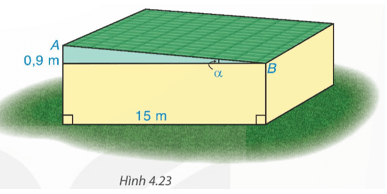
Ta có: \(\tan \alpha = \frac{{0,9}}{{15}}\) hay \(\alpha \approx {3^0}26'\)
Độ dài cạnh AB là AB = \(\sqrt {0,{9^2} + {{15}^2}} = \sqrt {225,81} \approx 15,03 m\)
Vậy góc nghiêng \alpha của mái nhà kho khoảng \({3^0}26'\) và chiều rộng \(AB \approx 15,03\)
Bài 4.11 trang 78 Toán 9 Tập 1:
Tính các góc của hình thoi có hai đường chéo dài \(2\sqrt 3\) và 2.
Hướng dẫn
Xét hình thoi ACBE có hai đường chéo ED và đường chéo AB lần lượt là \(2\sqrt 3\) và 2.
Hai đường chéo cắt nhau tại C nên C là trung điểm của hai đường chéo
Do đó: \(CE = CD = \sqrt 3\) ;AC = CB = 1
Tam giác ACD vuông tại C (tính chất hai đường chéo của hình thoi) ta có:
\(CE = CD = \sqrt 3\) hay \(\widehat {DAC} = {60^0}\) nên \(\widehat {DAE} = 2\widehat {DAC} = {2.60^0} = {120^0}\) (tính chất hình thoi)
\(\widehat {DAC} + \widehat {ADC} = {90^0}\) (Do tam giác ACD vuông tại C)
Nên\(\widehat {ADC} = {90^0} - {60^0} = {30^0}\) nên \(\widehat {ADB} = 2.\widehat {ADC} = {2.30^0} = {60^0}\)
Vậy hình thoi có các góc là 1200 và 600
Bài 4.12 trang 78 Toán 9 Tập 1:
Cho hình thang ABCD (AD // BC) có AD = 16cm,BC = 4cm,\(\widehat A = \widehat B = \widehat {ACD} = {90^0}.\)
a) Kẻ đường cao CE của tam giác ACD. Chứng minh \widehat {ADC} = \widehat {ACE}. Tính sin của các góc \widehat {ADC},\widehat {ACE} và suy ra A{C^2} = AE.AD. Từ đó tính AC.
b) Tính góc D của hình thang.
Hướng dẫn
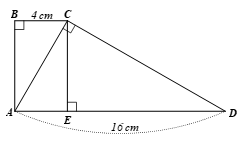
a) Ta có \(\widehat {ADC} = \widehat {ACE}\) (cùng phụ với góc DCE)
Ta có \(\sin \widehat {ADC} = \frac{{AC}}{{AD}};\sin \widehat {ACE} = \frac{{AE}}{{AC}}\). Từ đó ta có \(\frac{{AC}}{{AD}} = \frac{{AE}}{{AC}}\) hay \(A{C^2} = AE.AD.\)
AECB là hình chữ nhật do \(\widehat {BAE} = \widehat {ABC} = \widehat {AEC} = {90^0}\) do đó ta có AE = BC = 4 cm.
Nên \(A{C^2} = AE.AD = 4.16 = 64\) hay \(AC = \sqrt {64} = 8 cm (vì AC > 0)\)
b) \(\sin \widehat {ADC} = \frac{{AC}}{{AD}}\) hay \(\sin \widehat {ADC} = \frac{8}{{16}} = \frac{1}{2}\) hay \(\sin \widehat {ADC} = {30^0}\)
Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24).
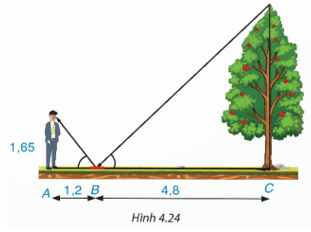
Hướng dẫn
Gọi D là điểm tại mắt của người đứng, E là điểm trên đầu ngọn cây, ta có hình vẽ sau;
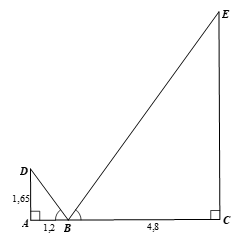
Chiều cao của cây là đoạn EC
Ta có \(\tan \widehat {ABD} = \frac{{1,65}}{{1,2}} = \frac{{11}}{8}\) hay \(\tan \widehat {EBC} = \frac{{11}}{8}\) (do\(\widehat {ABC} = \widehat {DBC})\)
Mà \(\tan \widehat {EBC} = \frac{{EC}}{{BC}}\) suy ra \(\frac{{EC}}{{4,8}} = \frac{{11}}{8}\) hay \(EC = \frac{{11}}{8}.4,8 = 6,6 m\)
Vậy chiều cao của cây là 6,6 m.
