Toán 9 Kết nối tri thức Luyện tập chung (trang 79)
Phần Luyện tập chung (trang 79) trong sách giáo khoa Toán 9 – Kết nối tri thức là cơ hội để học sinh ôn tập, hệ thống hóa và củng cố kiến thức đã học về đường tròn, tam giác, các yếu tố hình học cơ bản cũng như kỹ năng giải bài toán tổng hợp. Thông qua các bài tập đa dạng, học sinh không chỉ rèn luyện tư duy logic mà còn nâng cao khả năng vận dụng linh hoạt các định lý, tính chất hình học. Dưới đây là phần giải chi tiết giúp các em nắm vững phương pháp và tự tin hoàn thành bài học một cách hiệu quả.
Mục lục bài viết
Bài 9.13 trang 79 Toán 9
Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng 
. Tính số đo các góc của tam giác ABC.
Lời giải:
Bài 9.14 trang 79 Toán 9
Cho ABC là tam giác đều có cạnh bằng 4 cm. Tính bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp tam giác ABC.
Lời giải:
Vẽ đường tròn (O) ngoại tiếp tam giác đều ABC.
Vì tam giác ABC đều nên đường tròn (O) có tâm là trọng tâm của tam giác và có bán kính là 
\(R=\frac{\sqrt{3}}{3}4=4\frac{\sqrt{3}}{3}\ \left(cm\right)\)
Mặt khác, ta đã biết đường tròn nội tiếp tam giác đều có tâm là trọng tâm của tam giác đó, nên trọng tâm O cũng là tâm đường tròn nội tiếp tam giác đó.
Khi đó bán kính đường tròn nội tiếp tam giác ABC là \(r=\frac{\sqrt{3}}{6}4=\frac{2\sqrt{3}}{3}\) cm.
Bài 9.15 trang 79 Toán 9
Cho tam giác đều ABC có cạnh bằng 3 cm và nội tiếp đường tròn (O) như Hình 9.26.
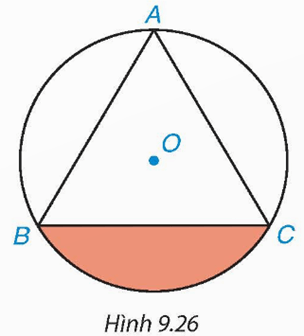
a) Tính bán kính R của đường tròn (O).
b) Tính diện tích hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC.
Lời giải:
a) Đường tròn (O) ngoại tiếp tam giác đều ABC nên có bán kính là \(R=\frac{\sqrt{3}}{3}3\ =\ \sqrt{3}\ \left(cm\right)\)
b)
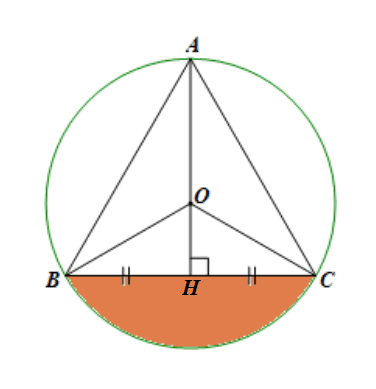
Do ∆ABC là tam giác đều nên \(\widehat {BAC} = \widehat {ABC}=60°\).
Xét đường tròn (O) có \(\widehat {BAC} = \widehat {BOC}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BC nên \(\widehat {BAC} = 1/2\widehat {BOC}\), suy ra \(\widehat {BOC} = 2\widehat {BAC} = 2\times60^{\circ} =120^{\circ}\)
Do đó cung nhỏ BC có số đo bằng 120°.
Diện tích hình quạt tròn bán kính R=√3cm ứng với cung nhỏ BC có số đo bằng 120° là:
\(Sq=n\pi R2360=120⋅\pi⋅(\sqrt{3})2360=\pi(cm2)\ S_q=\frac{n\pi R^2}{360}=\frac{120\pi\left(\sqrt{3}\right)^2}{360}=\pi\ \left(cm^2\right)\)
Gọi H là giao điểm của AO và BC. Khi đó AH vừa là đường trung trực, vừa là đường phân giác, cũng là đường cao của tam giác.
Vì BO là phân giác của góc ABC nên \(\widehat {OBH} = \frac{1}{2} \widehat {ABC}= \frac{1}{2} 60°=30^{\circ}\).
Xét ∆OBH vuông tại H, có:
\(O
H
=
O
B
⋅
sin
\widehat {BOH}
=
R
⋅
sin
30
°
=
√
\frac{3}{2}
(cm).\)
Diện tích của tam giác OBC là:
\(S_{OBC}=\frac{1}{2}OH⋅BC=\frac{12⋅\sqrt{3}}{2}3=3\sqrt{\frac{3}{4}}(cm2).\)
Gọi S là diện tích viên phân giới hạn bởi dây cung BC và cung nhỏ BC.
Ta có: S=SOBC−Sq=π−\(3\sqrt{\frac{3}{4}}\)(cm2).
Vậy hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC có diện tích bằng π−\(3\sqrt{\frac{3}{4}}\)(cm2).
