Toán 9 Kết nối tri thức Luyện tập chung (trang 106, 107)
Giải Toán 9 – Luyện tập chung (trang 106, 107) – Kết nối tri thức giúp học sinh ôn tập toàn diện các kiến thức hình học không gian đã học trong chương, bao gồm hình trụ, hình nón và hình cầu. Với lời giải chi tiết, rõ ràng và dễ hiểu, tài liệu hỗ trợ học sinh rèn luyện kỹ năng tính toán, củng cố kiến thức và chuẩn bị tốt cho các bài kiểm tra. Đây là nguồn tham khảo hữu ích dành cho học sinh lớp 9 trong quá trình học và ôn luyện theo chương trình sách mới.
Mục lục bài viết
Bài 10.11 trang 106
Cho một hình trụ có đường kính của đáy bằng với chiều cao và có thể tích bằng 2π cm3.
a) Tính chiều cao của hình trụ.
b) Diện tích toàn phần của hình trụ bằng tổng diện tích xung quanh và diện tích hai đáy hình trụ. Tính diện tích toàn phần của hình trụ trên.
Lời giải:
a) Gọi R (cm) là đường kính đáy của hình trụ (R > 0).
Khi đó, bán kính đáy của hình trụ là R2 (cm) và chiều cao là R (cm).
Thể tích hình trụ là: V=π⋅(
\(\frac{R}{2}\))2⋅R=\(\frac{R^3\pi}{4}\)(cm3).
Vì thể tích hình trụ bằng 2π cm3 nên ta có: \(\frac{R^3\pi}{4}\)=2π.
Suy ra R3 = 8 nên R = 2 cm (do R > 0).
Vậy chiều cao hình trụ là h = 2 cm.
b) Diện tích xung quanh của hình trụ bán kính 1 cm và chiều cao 2 cm là:
Sxq = 2π . 1 . 2 = 4π (cm2).
Diện tích hai đáy của hình trụ bán kính 1 cm là:
S1 = 2π . 1.2 = 2π (cm2).
Diện tích toàn phần của hình trụ là:
S = Sxq + S1 = 4π + 2π = 6π (cm2).
Vậy diện tích toàn phần của hình trụ là 6π cm2.
Bài 10.12 trang 107
Một vòng bi bằng thép có hình dạng (phần thép giữa hai hình trụ) và kích thước như Hình 10.30. Tính thể tích của vòng bi đó.
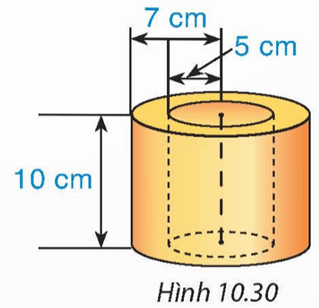
Lời giải:
Thể tích hình trụ có bán kính 7 cm, chiều cao 10 cm là:
V1 = π . 72 . 10 = 490π (cm3).
Thể tích hình trụ có bán kính 5 cm, chiều cao 10 cm là:
V2 = π . 52 . 10 = 250π (cm3).
Thể tích của vòng bi là:
V = V1 − V2 = 490π − 250π = 240π (cm3).
Vậy thể tích của vòng bi đó là 240π cm3.
Bài 10.13 trang 107
Chiếc mũ của chú hề với các kích thước như Hình 10.31. Hãy tính tổng diện tích vải cần để làm chiếc mũ (coi mép khâu không đáng kể và làm tròn kết quả đến hàng phần mười của cm2).
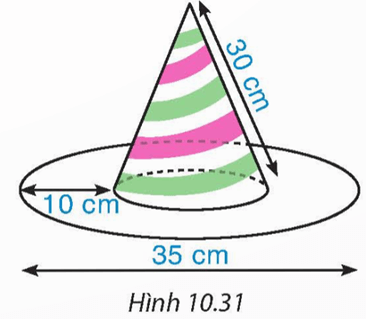
Lời giải:
Bán kính đường tròn đáy của hình nón là:
r=\(\frac{35−2⋅10}{2}\)=7,5(cm).
Diện tích xung quanh hình nón là:
Sxq = πrℓ = π . 7,5 . 30 = 225π (cm2).
Diện tích vành nón là:
S1 = π . 17,52 – π . 7,52 = 250π (cm2).
Diện tích vải cần dùng là:
S = Sxq + S1 = 225π + 250π = 475π ≈ 1 492,3 (cm2).
Vậy tổng diện tích vải cần để làm chiếc mũ khoảng 1 492,3 cm2.
Bài 10.14 trang 107
Người ta nhấn chìm hoàn toàn 5 viên bi có dạng hình cầu vào một chiếc cốc hình trụ đựng đầy nước, mỗi viên bi có đường kính 2 cm. Tính lượng nước tràn ra khỏi cốc.
Lời giải:
Bán kính mỗi viên bi là: R=\(\frac{2}{2}\)=1(cm).
Thể tích nước tràn ra khỏi cốc bằng thể tích của 5 viên bi nên thể tích nước tràn ra ngoài là:
5⋅\(\frac{4}{3}\)π⋅13=\(\frac{20}{3}\)π(cm3).
Vậy lượng nước tràn ra khỏi cốc bằng \(\frac{20}{3}\)πcm3.
Bài 10.15 trang 107
Một bồn chứa xăng gồm hai nửa hình cầu có đường kính bằng 1,8 m và một hình trụ có chiều cao bằng 3,6 m (H.10.32). Tính thể tích của bồn chứa xăng (làm tròn kết quả đến hàng trăm của m3).
Lời giải:
Bán kính hai nửa hình cầu là: \(\frac{1,8}{2}\)=0,9(m).
Thể tích hình trụ chiều cao 3,6 m và bán kính 0,9 m là:
V1 = π . 0,92 . 3,6 = 2,916π (m3).
Thể thể tích hai nửa hình cầu bán kính 0,9 m là:
V2=\(\frac{4}{3}\)⋅π⋅0,93=0,972π(m3).
Thể tích bồn chứa xăng là:
V = V1 + V2 = 2,916π + 0,972π = 3,888π ≈ 12,21(m3).
Vậy thể tích của bồn chứa xăng khoảng 12,21 m3.
Bài 10.16 trang 107
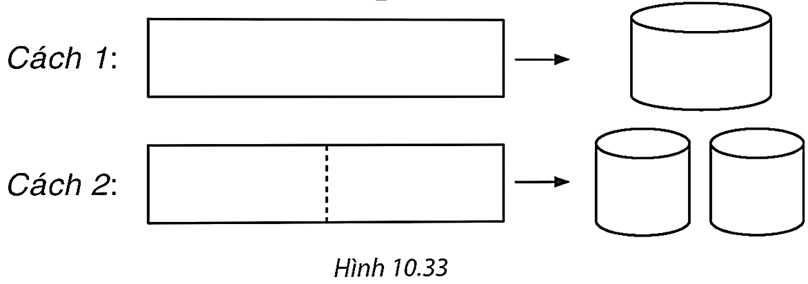
Từ một tấm tôn hình chữ nhật có kích thước 50 cm × 240 cm, người ta làm mặt xung quanh của các thùng đựng nước hình trụ có chiều cao bằng 50 cm, theo hai cách sau (H.10.33):
• Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng nước hình trụ.
• Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau hình chữ nhật, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu V1 là thể tích của thùng gò theo Cách 1 và V2 là tổng thể tích của hai thùng gò được theo Cách 2. Tính tỉ số V1V2 (giả sử các mối hàn là không đáng kể).
Lời giải:
• Theo Cách 1, chu vi đường tròn đáy bằng 240 cm, ta có: 2πR1 = 240 nên R1=\(\frac{120}{\pi}\)cm.
Thể tích của thùng gò hình trụ là:
V1=π⋅(\(\frac{120}{\pi}\))2⋅50=\(\frac{720000}{\pi}\)(cm3).
• Theo Cách 2, chu vi đường tròn đáy bằng 120 cm, ta có: 2πR2 = 120 nên R2=\(\frac{60}{\pi}\)cm.
Tổng thể tích hai hình trụ gò được là:
V2=π⋅(\(\frac{60}{\pi}\))2⋅50=\(\frac{360000}{\pi}\)(cm3).
Do đó, V1V2=\(\frac{720000}{\pi}\):\(\frac{360000}{\pi}\)=2.
Vậy V1V2=2.
