Giải Toán 9 trang 8 tập 2 Kết nối tri thức
Giải Toán 9 trang 8 Tập 2
Trong chương trình Toán 9 – Kết nối tri thức, các bài học đầu tập 2 giữ vai trò quan trọng trong việc hình thành và củng cố kiến thức nền tảng cho học sinh. Đặc biệt, nội dung Giải Toán 9 trang 8 tập 2 thường được nhiều học sinh và phụ huynh tìm kiếm nhằm kiểm tra kết quả, hiểu rõ phương pháp làm bài và tránh những sai sót cơ bản.
Bài viết Giải Toán 9 trang 8 tập 2 Kết nối tri thức được biên soạn chi tiết, bám sát SGK, trình bày lời giải rõ ràng, dễ hiểu, giúp học sinh không chỉ có đáp án đúng mà còn nắm vững cách tư duy và vận dụng kiến thức hiệu quả.
Luyện tập 2 trang 8 Toán 9 Tập 2 Kết nối
Vẽ đồ thị của hàm số 
. Tìm các điểm thuộc đồ thị có tung độ bằng 2 và nhận xét về tính đối xứng giữa các điểm đó.
Hướng dẫn giải:
a) Lập bảng một số giá trị tương ứng giữa x và y:
| x | – 2 | – 1 | 0 | 1 | 2 |
|
2 | |
0 | |
2 |
Biểu diễn các điểm (– 2; 2), (– 1; ), (0; 0), (1; ) và (2; 2) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị của hàm số như hình sau:
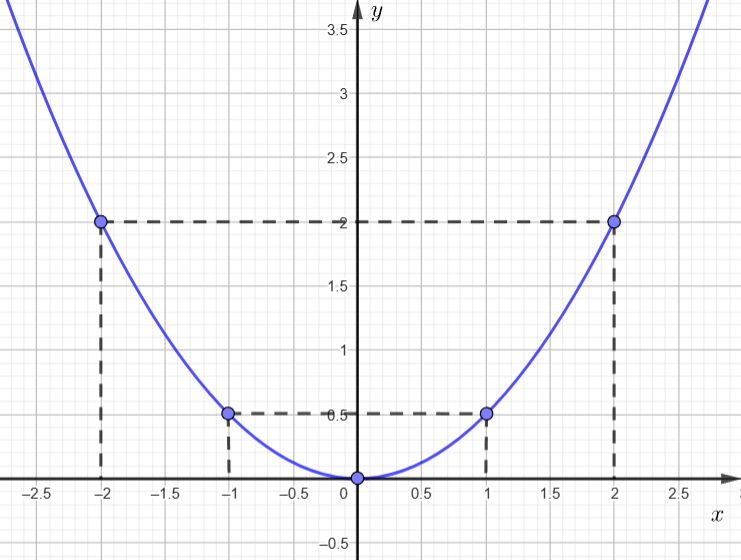
b) Ta có: y = 2 nên hay x2 = 4
⇒ x = 2 hoặc x = – 2
Vậy có hai điểm cần tìm là (2; 2) và (–2; 2). Hai điểm này đối xứng với nhau qua trục tung Oy.
Vận dụng 2 trang 8 Toán 9 Tập 2 Kết nối
Giải quyết bài toán ở tình huống mở đầu.
Tình huống: Một cây cầu treo có trụ tháp đôi cao 75 m so với mặt của cây cầu và cách nhau 400 m. Các dây cáp có dạng đồ thị của hàm số y = ax2 (a ≠ 0) như Hình 6.1 và được treo trên các đỉnh tháp. Tìm chiều cao CH của dây cáp biết điểm H cách tâm O của cây cầu 100 m (giả sử mặt của cây cầu là bằng phẳng).
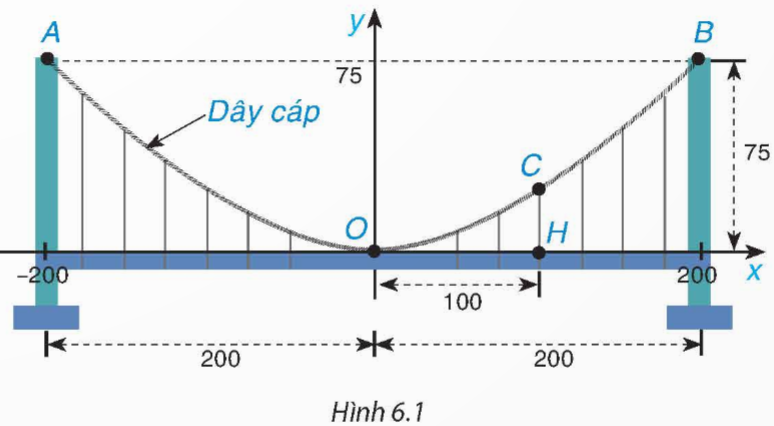
Hướng dẫn giải:
Vì các dây cáp có dạng đồ thị của hàm số y = ax2 (a ≠ 0) được treo trên các đỉnh tháp nên đồ thị hàm số y = ax2 (a ≠ 0) đi qua điểm B(200; 75).
⇒ 75 = a . 2002
⇒ 40 000a = 75
⇒ a = 0,001875 (tmđk).
Khi đó hàm số có dạng
Do đó chiều cao CH của dây cáp chính là tung độ của điểm C(100; CH) trên đồ thị hàm số
⇒ (m)
Bài 6.1 trang 8 Toán 9 Tập 2 Kết nối
Cho hàm số y = 0,25x2. Hoàn thành bảng giá trị sau vào vở:
Hướng dẫn giải:
Ta có bảng giá trị:
|
x |
– 3 |
– 2 |
– 1 |
0 |
1 |
2 |
3 |
|
y = 0,25x2 |
2,25 |
1 |
0,25 |
0 |
0,25 |
1 |
2,25 |
Bài 6.2 trang 8 Toán 9 Tập 2 Kết nối
Cho hình lăng trụ đứng có đáy là hình vuông cạnh a (cm) và chiều cao 10 cm.
a) Viết công thức tính thể tích V của lăng trụ theo a và tính giá trị của V khi a = 2 cm.
b) Nếu độ dài cạnh đáy tăng lên hai lần thì thể tích của hình lăng trụ thay đổi thế nào?
Hướng dẫn giải:
a) Thể tích V của hình lăng trụ đứng là:
V = B . h = 10a2 (cm3)
Tại a = 2 cm, ta có:
V = 10 . 22 = 40 (cm3)
b) Nếu độ dài cạnh đáy tăng lên hai lần thì diện tích đáy tăng lên 4 lần
Khi đó V' = B' . h = 4a2 . 10 = 40a2 = 4V
Vậy nếu độ dài cạnh đáy tăng lên hai lần thì thể tích của hình lăng trụ tăng lên 4 lần.
Bài 6.3 trang 8 Toán 9 Tập 2 Kết nối
Diện tích toàn phần S (cm2) của hình lập phương, tức là tổng diện tích xung quanh và diện tích của hai mặt đáy là một hàm số của độ dài cạnh a (cm).
a) Viết công thức của hàm số này.
b) Sử dụng công thức nhận được ở câu a để tính độ dài cạnh của một hình lập phương có diện tích toàn phần là 54 cm2.
Hướng dẫn giải:
a) Diện tích toàn phần của hình lập phương hay công thức của hàm số là:
S = 6a2 (cm2)
b) Diện tích toàn phần của hình lập phương là 54 cm2, ta có:
6a2 = 54
⇒ a2 = 9
⇒ a = 3 (a > 0)
Vậy độ dài cạnh bằng 3 cm thì hình lập phương có diện tích toàn phần là 54 cm2.
Bài 6.4 trang 8 Toán 9 Tập 2 Kết nối
Vẽ đồ thị của các hàm số sau:
a) y = 3x2
b)
Hướng dẫn giải:
a) y = 3x2
Lập bảng một số giá trị tương ứng giữa x và y:
| x | – 2 | – 1 | 0 | 1 | 2 |
| y = 3x2 | 12 | 3 | 0 | 3 | 12 |
Biểu diễn các điểm (– 2; 12), (– 1; 3), (0; 0), (1; 3) và (2; 12) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị của hàm số như hình sau:
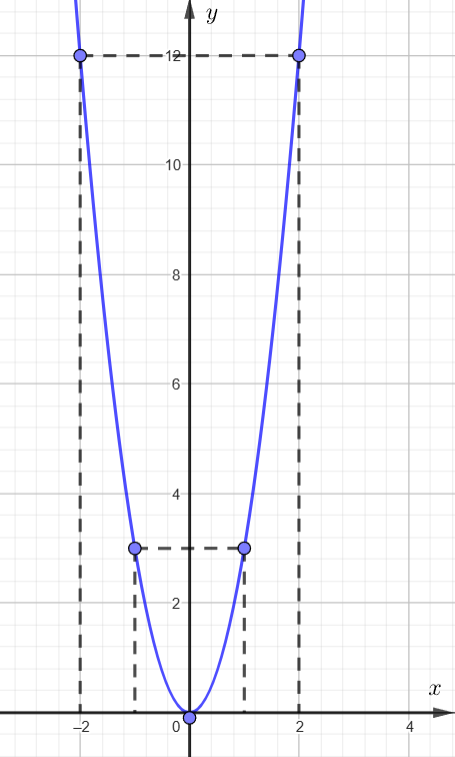
b)
Lập bảng một số giá trị tương ứng giữa x và y:
| x | – 2 | – 1 | 0 | 1 | 2 |
|
|
|
0 | |
|
Biểu diễn các điểm (– 2; ), (– 1; ), (0; 0), (1; ) và (2; ) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị của hàm số như hình sau:
Bài 6.5 trang 8 Toán 9 Tập 2 Kết nối
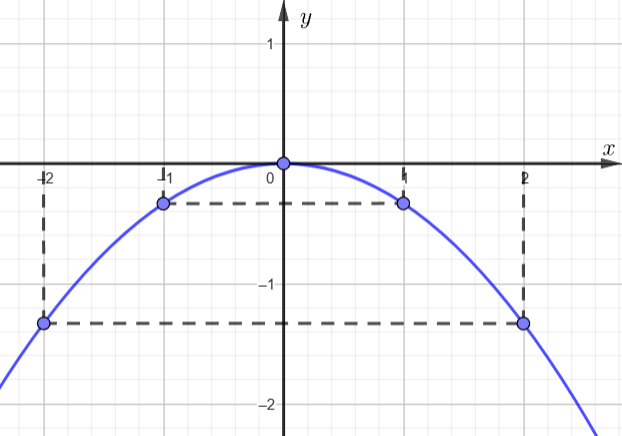
Biết rằng đường cong trong Hình 6.6 là một parabol y = ax2.
a) Tìm hệ số a.
b) Tìm tung độ của điểm thuộc parabol có hoành độ x = – 2.
c) Tìm các điểm thuộc parabol có tung độ y = 8.
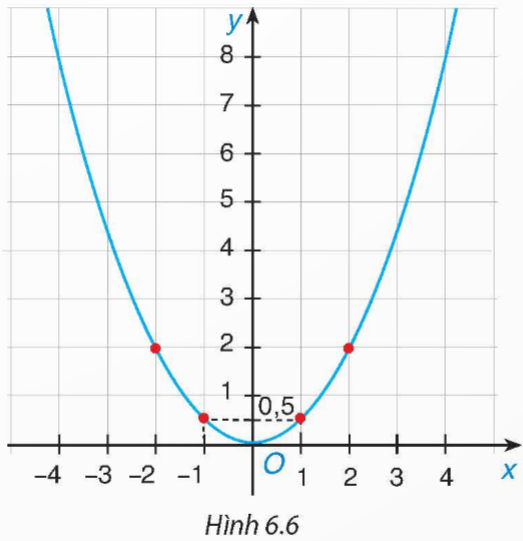
Hướng dẫn giải:
a) Trong Hình 6.6 ta thấy đồ thị hàm số y = ax2 đi qua điểm (2; 2)
⇒ 2 = a . 22
⇒ 4a = 2
⇒ a =
b) Quan sát đồ thị hàm số, ta có tung độ của điểm thuộc parabol có hoành độ x = – 2 là 2.
c) Từ câu a ta có đồ thị của hàm số
Ta có y = 8 nên
⇒ x2 = 16.
⇒ x = 4 hoặc x = – 4.
Vậy có hai điểm cần tìm là (– 4; 8) và (4; 8).
-----------------------------------------------
Thông qua việc tham khảo lời giải SGK Toán 9 KNTT trang 8, học sinh sẽ củng cố kiến thức đã học, rèn luyện kỹ năng trình bày và nâng cao khả năng tự học tại nhà. Việc hiểu rõ từng bước giải không chỉ giúp làm tốt bài tập hiện tại mà còn tạo nền tảng vững chắc cho các nội dung tiếp theo trong chương trình Toán 9.
Hy vọng bài viết sẽ trở thành tài liệu tham khảo đáng tin cậy, hỗ trợ học sinh học tốt Toán và đạt kết quả cao trong các bài kiểm tra, đánh giá định kỳ.
