Toán 9 Kết nối tri thức Luyện tập chung (trang 91)

Giải Toán 9 Kết nối tri thức – Luyện tập chung (trang 91) cung cấp lời giải chi tiết, dễ hiểu cho các bài tập tổng hợp sau chương. Đây là phần quan trọng giúp học sinh hệ thống lại kiến thức, rèn luyện tư duy giải toán và chuẩn bị tốt cho các bài kiểm tra. Với cách trình bày khoa học, rõ ràng, nội dung sẽ hỗ trợ học sinh lớp 9 học tập hiệu quả và tự tin hơn khi làm bài.

Bài 9.31 trang 91 Toán 9 

Cho tam giác ABC có các đường cao AD, BE, CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.

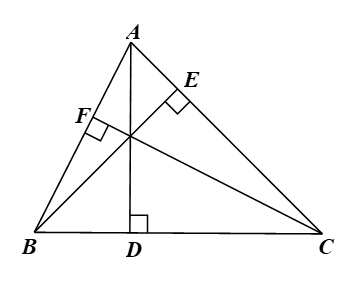
Lời giải:

⦁ Vì ∆BEC vuông tại E (do BE ⊥ AC) nên tam giác có đường tròn ngoại tiếp đường tròn đường kính BC. Do đó ba điểm B, E, C cùng nằm trên đường tròn đường kính BC.

Vì ∆BFC vuông tại F (do CF ⊥ AB) nên tam giác có đường tròn ngoại tiếp là đường tròn đường kính BC. Do đó ba điểm B, F, C cùng nằm trên đường tròn đường kính BC.

Suy ra bốn điểm B, C, E, F cùng nằm trên một đường tròn hay tứ giác BCEF là tứ giác nội tiếp.

⦁ Chứng minh tương tự, ta cũng có tứ giác CAFD nội tiếp đường tròn đường kính AC và tứ giác ABDE nội tiếp đường tròn đường kính AB.

Vậy BCEF, CAFD, ABDE là những tứ giác nội tiếp.

Bài 9.32 trang 91 Toán 9

Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như Hình 9.58. Biết \(\widehat {BEC}\)=40° và \(\widehat {DFC}\)=20°, tính số đo các góc của tứ giác ABCD.

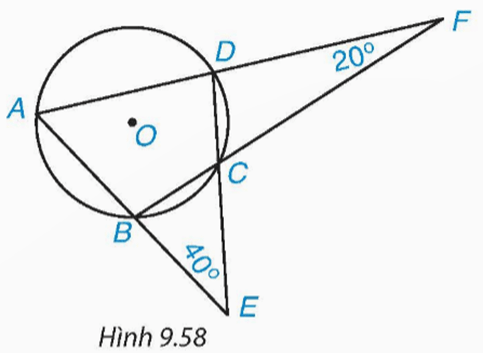
Lời giải:

Xét ∆ABF có \(\widehat {A}+\widehat {ABF}+\widehat {F}\)=180° (tổng ba góc của tam giác)

Do đó \(\widehat {ABF}=180^{\circ} -\widehat {F}-\widehat {A}=180^{\circ} -20^{\circ} -\widehat {A}=160^{\circ} -\widehat {A} ˆABF=180°−ˆF−ˆA=180°−20°−ˆA=160°−ˆA\)

Xét ∆ADE có \(\widehat {A}+\widehat {ADE}+\widehat {E}\)=180° (tổng ba góc của tam giác)

Do đó \(\widehat {ADE}=180^{\circ} -\widehat {E}-\widehat {A}=180^{\circ} -40^{\circ} -\widehat {A} =140^{\circ} -\widehat {A}\).

Vì ABCD là tứ giác nội tiếp đường tròn (O) nên tổng các góc đối nhau của tứ giác bằng 180°, do đó \(\widehat {A}+\widehat {BCD}\)=180°, suy ra\(\widehat {BCD} = 180^{\circ} -\widehat {A}\).

Xét tứ giác ABCD có:

\(\widehat {A}+\widehat {ABC}+\widehat {BCD}+\widehat {ADC}\)=360° (tổng các góc của một tứ giác)

Suy ra\(\widehat {A}+(160^{\circ}-\widehat {A})+(180^{\circ} -\widehat {A})+(140^{\circ} -\widehat {A})=360^{\circ}\)

Hay \(2\widehat {A}=120°\), nên \(\widehat {A}=60^{\circ}\)°.

Do đó \(\widehat {ABC}=160^{\circ} - \widehat {A}\)=160°−60°=100°;

\(\widehat {ADC}=140^{\circ} -\widehat {A}\)=140°−60°=80°;

\(\widehat {BCD}=180^{\circ} -\widehat {A}\)=180°−60°=120°.

Vậy tứ giác ABCD có \(\widehat {A}=60°;\widehat {ABC}=100°;\widehat {BCD}=120°;\widehat {ADC}=80°\).

Bài 9.33 trang 91 Toán 9 

Cho hình vuông ABCD có cạnh bằng 4 cm. Tính chu vi, diện tích của các đường tròn nội tiếp và ngoại tiếp hình vuông ABCD.

Lời giải:

Gọi R là bán kính đường tròn ngoại tiếp hình vuông ABCD.

Khi đó ta có R = 1/2AC.

Xét ∆ABC vuông tại B (do ABCD là hình vuông), theo định lí Pythagore, ta có:

AC² = AB² + BC² = 4² + 4² = 32.

Do đó AC = √32=4√2 (cm).

Suy ra R=\(\frac{1}{2}\)AC=\(\frac{1}{2}\)⋅4√2=2√2(cm).

Chu vi của đường tròn ngoại tiếp hình vuông ABCD là:

2πR=2π⋅2√2=4π√2(cm).

Diện tích của đường tròn ngoại tiếp hình vuông ABCD là:

πR2=π⋅(2√2)²=8π(cm²).

Gọi r là bán kính đường tròn nội tiếp hình vuông ABCD.

Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA.

Vì ABCD là hình vuông nên hai đường chéo AC, BD vuông góc với nhau tại trung điểm O của mỗi đường.

Xét ∆OAB vuông tại O có OM là đường trung tuyến ứng với cạnh huyền nên OM = 12AB.

Mặt khác, ∆OAB cân tại O (vì OA = OB) nên đường trung tuyến OM đồng thời là đường cao, do đó OM ⊥ AB tại M.

Tương tự, ta có:

⦁ ON ⊥ BC tại N, OP ⊥ CD tại P, OQ ⊥ AD tại Q.

⦁ ON = 12BC, OP = 12CD, OQ = 12DA.

Mà AB = BC = CD = DA (do ABCD là hình vuông)

Nên OM = ON = OP = OQ.

Vậy đường tròn (O; OM) là đường tròn nội tiếp hình vuông ABCD.

Khi đó ta có r = OM = 1/2AB = 1/2.4 = 2 (cm).

Chu vi của đường tròn nội tiếp hình vuông ABCD là:

2πr = 2π.2 = 4π (cm).

Diện tích của đường tròn nội tiếp hình vuông ABCD là:

πr² = π.2² = 4π (cm²).

Bài 9.34 trang 91 Toán 9 

Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều quay của kim đồng hồ. Phép quay thuận chiều 45° biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H.

a) Vẽ đa giác EAFBGCHD.

b) Đa giác EAFBGCHD có phải là một bát giác đều hay không? Vì sao?

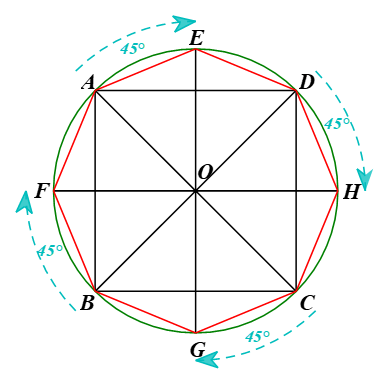
Lời giải:

a)

⦁ Vẽ đường tròn (O). Trên đường tròn (O) vẽ hình vuông ABCD sao cho các đỉnh ABCD sao cho các đỉnh A, B, C, D theo thứ tự ngược chiều kim đồng hồ.

⦁ Lấy điểm E thuộc đường tròn (O) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OE và \(\widehat {AOE}\)=45°.

⦁ Xác định các điểm F, G, H tương tự như cách xác định điểm E ở trên. Nối A với E, E với D, D với H, H với C, C với G, G với B, B với F và F với A. Khi đó ta được đa giác EAFBGCHD.

b) Vì ABCD là hình vuông nên đường tròn (O) ngoại tiếp hình vuông có tâm O là giao điểm hai đường chéo. Do đó AC ⊥ BD tại O hay \(\widehat {AOD}\)=90°.

Suy ra\(\widehat {AOE} +\widehat {EOD}\)=90°, suy ra \(\widehat {AOE} = 90^{\circ} - \widehat {EOD}\)=90°−45°=45°.

Xét ∆OAE và ∆OED có:

OA = OE, \(\widehat {AOE} = \widehat {EOD}\) (cùng bằng 45°), OE = OD.

Do đó ∆OAE = ∆OED (c.g.c).

Tương tự, ta sẽ chứng minh được:

∆OAE = ∆OED = ∆ODH = ∆OHC = ∆OCG = ∆OGB = ∆OBF = ∆OFA.

Suy ra:

⦁ AE = ED = DH = HC = CG = GB = BF = FA; (1)

⦁ \(\widehat {OAE}=\widehat {OED}=\widehat {ODH}=\widehat {OHC}=\widehat {OCG}=\widehat {OGB}=\widehat {OBF}=\widehat {OFA}\);

⦁ \(\widehat {OEA}=\widehat {ODE}=\widehat {OHD}=\widehat {OCH}=\widehat {OGC}=\widehat {OBG}=\widehat {OFB}=\widehat {OAF}\).

Xét ∆OAE có OA = OE nên ∆OAE cân tại O, suy ra \(\widehat {OAE}=\widehat {OEA}\).

Suy ra \(\widehat {OAE}+\widehat {OAF}=\widehat {OED}+\widehat {OEA}=\widehat {ODH}+\widehat {ODE}=\widehat {OHC}+\widehat {OHD}\)

=\(\widehat {OCG}+\widehat {OCH}=\widehat {OGB}+\widehat {OGCD}=\widehat {OBF}+\widehat {OBG}=\widehat {OFA}+\widehat {OFB}\).

Hay\(\widehat {EAF}=\widehat {AFB}=\widehat {FBG}=\widehat {BGC}=\widehat {GCH}=\widehat {CHD}=\widehat {HDE}=\widehat {DEA}\).(2)

Từ (1) và (2) suy ra EAFBGCHD có các cạnh bằng nhau và các góc bằng nhau.

Vậy EAFBGCHD là bát giác đều.