Toán 9 Kết nối tri thức Bài 30: Đa giác đều

Với lời giải chi tiết và dễ hiểu cho Bài 30: Đa giác đều – SGK Toán 9 (Kết nối tri thức), tài liệu này sẽ giúp học sinh lớp 9 nắm vững kiến thức và rèn luyện kỹ năng giải bài tập hình học một cách hiệu quả. Nội dung được trình bày theo từng trang sách (trang 87, 88, 89), phù hợp để học sinh tra cứu, tham khảo khi học trên lớp hoặc tự học tại nhà. Đây sẽ là trợ thủ đắc lực giúp các em học tốt môn Toán 9 và đạt điểm cao trong các bài kiểm tra.

Bài 9.24 trang 89 Toán 9

Trong các hình phẳng sau (H.9.52), hình nào là hình phẳng có dạng đa giác đều?

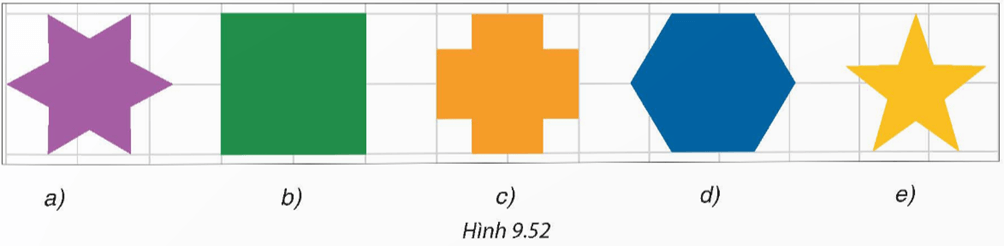
Lời giải:

Hình b là hình vuông, hình d là hình lục giác đều vì hai hình đều có các cạnh bằng nhau và các góc bằng nhau.

Trong các hình dưới đây (H.9.53), hình nào vẽ hai điểm M và N thỏa mãn phép quay thuận chiều 60° tâm O biến điểm M thành điểm N?

Bài 9.25 trang 89 Toán 9

Trong các hình dưới đây (H.9.53), hình nào vẽ hai điểm M và N thỏa mãn phép quay thuận chiều 60° tâm O biến điểm M thành điểm N?

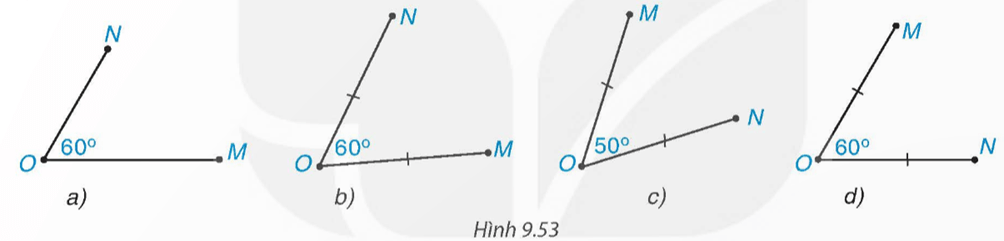
Lời giải:

Phép quay thuận chiều 60° tâm O biến điểm M thành điểm N tức là điểm N thuộc đường tròn (O; OM) sao cho tia OM quay thuận kim đồng hồ đến tia ON và điểm M tạo nên cung MN có số đo là 60°.

Trong các hình đã cho, hình d là hình cần tìm.

Bài 9.26 trang 89 Toán 9 

Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2 cm. Tính độ dài các cạnh của tam giác ABC.

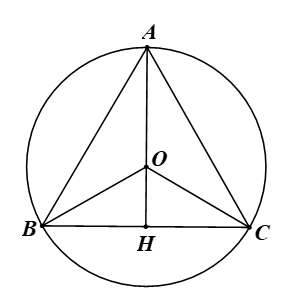
Lời giải:

Vì tam giác đều ABC nội tiếp đường tròn (O) bán kính 2 cm nên ta có OA = OB = OC = 2 cm.

Vì ABC là tam giác đều nên tâm O của đường tròn ngoại tiếp tam giác là trọng tâm của tam giác.

Gọi H là giao điểm của AO và BC. Khi đó AH vừa là đường trung trực, vừa đường cao, vừa là đường trung tuyến của tam giác.

Do đó

\(AO=\frac{2}{3}AH\ suy\ ra\ AH=\frac{3}{2}AO=\frac{3}{2}2=3\ \left(cm\right)\)

Vì ∆ABC đều nên \(\widehat {ABC}=60^{\circ}\)°.

Xét ∆ABH vuông tại H, ta có:

\(BH=\frac{AH}{tan\widehat {ABH}} = \frac{3}{tan60^{\circ} } = \frac{3}{\sqrt{3} } =\sqrt{3}\)

Vì AH là đường trung tuyến của ∆ABC nên H là trung điểm của BC, do đó BC = 2BH = 2√3 (cm)

Vậy các cạnh của tam giác ABC có độ dài bằng 2√3 cm.

Bài 9.27 trang 89 Toán 9

Cho hình thoi ABCD có ˆA=60°. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.

Lời giải:

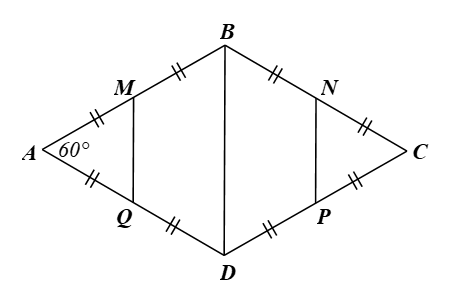
Vì ABCD là hình thoi nên AB = BC = CD = DA.

Vì M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên MA = MB = 12AB; NB = NC = 12BC; PC = PD = 12CD; QD = QA = 12DA.

Do đó AM = MB = NB = NC = PC = PD = QD = QA = 12AB. (1)

Xét ∆ABD có AB = AD nên ∆ABD cân tại A, lại có ˆA=60° nên ∆ABD là tam giác đều. Do đó AB = BD (2) và \(\widehat {ABD} = \widehat {ADB} = 60^{\circ}\).

Lại có M, Q là lần lượt là trung điểm của AB, AD nên MQ là đường trung bình của tam giác. Do đó MQ // BD và MQ = 12BD. (3)

Chứng minh tương tự, ta cũng có NP = 12BD. (4)

Từ (1), (2), (3) và (4) suy ra MB = BN = NP = PD = DQ = QM.

⦁ Vì MQ // BD nên \(\widehat {AMQ} = \widehat {ABD}= 60^{\circ}\) (so le trong).

Mà ˆAMQ+ˆBMQ=180° (hai góc kề bù)

Suy ra \(\widehat {BMQ}=180^{\circ} -\widehat {AMQ} = 180 ^{\circ} - 60^{\circ} = 120^{\circ}\).

Tương tự, ta có \(\widehat {BNP} = \widehat {NPD} = \widehat {DQM} = 120^{\circ}\).

Tam giác BCD có BC = CD và \(\widehat {C} = \widehat {A} = 60^{\circ}\) (tính chất hình thoi) nên ∆BCD là tam giác đều. Do đó ˆCBD=ˆCDB=60°.

Ta có \(\widehat {ABC} = \widehat {ABD} + \widehat {CBD} = 60^{\circ} + 60 ^{\circ}\);

\(\widehat {ADC} = \widehat {ADB} + \widehat {CDB} = 60^{\circ} + 60 ^{\circ}\)=120⁰

Khi đó, \(\widehat {MBN} = \widehat {BNP} = \widehat {NPD}= \widehat {PDQ}= \widehat {DQM}=120^{\circ}\)

Như vậy MBNPDQ có các cạnh bằng nhau và các góc bằng nhau.

Vậy MBNPDQ là lục giác đều.

Bài 9.28 trang 89 Toán 9 

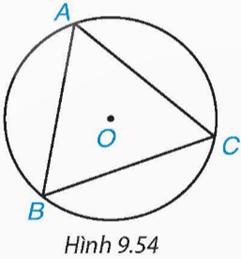
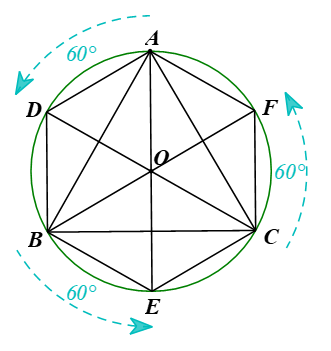
Cho tam giác đều ABC nội tiếp đường tròn (O) như Hình 9.54. Phép quay ngược chiều 60° tâm O biến các điểm A, B, C lần lượt thành các điểm D, E, F. Chứng minh rằng ADBECF là một lục giác đều.

Lời giải:

⦁ Vì ∆ABC là tam giác đều nên \(\widehat {BAC}=\widehat {ABC}=\widehat {ACB}=60^{\circ}\).

Xét đường tròn (O) có \(\widehat {ACB}, \widehat {AOB}\)lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung AB nên \(\widehat {ACB}=\frac{1}{2} \widehat {AOB}\), suy ra \(\widehat {AOB} = 2\widehat {ACB} = 2.60^{\circ} = 120^{\circ}\).

⦁ Vì phép quay ngược chiều 60° tâm O biến điểm A thành các điểm D nên điểm D nằm trên đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OD thì điểm A tạo nên cung AD có số đo 60°.

Khi đó ta có OA = OD và \(\widehat {AOD} = 60^{\circ}\) nên ∆OAD là tam giác đều.

Suy ra AD = OA = OD và \(\widehat {ODA} = 60^{\circ}\)(1)

⦁ Mặt khác,  \(\widehat {A O B} = \widehat {A O D} + \widehat {B O D}\)(hai góc kề nhau)

Nên\(\widehat {BOD} = \widehat {AOB} - \widehat {AOD}\)=120°−60°=60°.

Xét ∆BOD có OB = OD (cùng bằng OA) và \(\widehat {BOD}\)=60° nên ∆BOD là tam giác đều.

Do đó BD = OB = OD và \(\widehat {ODB}\)=60°.(2)

Từ (1) và (2) ta có AD = DB và \(\widehat {ADB} = \widehat {ODA} +\widehat {ODB}\)=60°+60°=120°.

Tương tự, ta sẽ chứng minh được:

AD = DB = BE = EC = CF = FA và \(\widehat {ADB} = \widehat {DBE} =\widehat {BEC} =\widehat {ECF}=\widehat {CFA}=\widehat {FAD}=120^{\circ}\).

Vậy ADBECF có các cạnh bằng nhau và các góc đều bằng 120° nên là một lục giác đều.