Toán 9 Kết nối tri thức bài 31: Hình trụ và hình nón
Giải Toán 9 – Bài 31: Hình trụ và hình nón (Kết nối tri thức) cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong bài học. Qua đó, học sinh sẽ nắm vững các kiến thức về hình học không gian như tính thể tích, diện tích xung quanh, diện tích toàn phần của hình trụ và hình nón. Tài liệu là công cụ hỗ trợ đắc lực giúp các em luyện tập hiệu quả, phát triển tư duy hình học và học tốt môn Toán 9 theo chương trình sách mới.
Mục lục bài viết
Bài 10.1 trang 100
Thay dấu “?” bằng giá trị thích hợp và hoàn thành bảng sau vào vở:
|
Hình |
Bán kính đáy (cm) |
Chiều cao (cm) |
Diện tích xung quanh (cm2) |
Thể tích (cm3) |
 |
4 |
6 |
? |
? |
|
3 |
5 |
? |
? |
|
|
? |
10 |
? |
50π |
|
|
8 |
? |
192π |
? |
Lời giải:
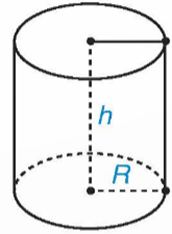
Hình vẽ trong bảng trên là hình trụ:
• Xét hình trụ có bán kính đáy là R = 4 cm và chiều cao h = 6 cm:
Diện tích xung quanh hình trụ là: Sxq = 2πRh = 2π . 4 . 6 = 48π (cm2).
Thể tích hình trụ là: V = πR2h = π . 42 . 6 = 96π (cm3).
• Xét hình trụ có bán kính đáy là R = 3 cm và chiều cao h = 5 cm:
Diện tích xung quanh hình trụ là: Sxq = 2πRh = 2π . 3 . 5 = 30π (cm2).
Thể tích hình trụ là: V = πR2h = π . 32 . 5 = 45π (cm3).
• Xét hình trụ có chiều cao h = 10 cm và thể tích 50π cm3:
Bán kính đáy của hình trụ là: R2=
\(\frac{V}{\pi h}\)=\(\frac{50\pi}{\pi10}\)=5⇒R=√5(cm).
Diện tích xung quanh hình trụ là: Sxq=2πRh=2π⋅√5⋅10=20√5π(cm2).
• Xét hình trụ có bán kính đáy là R = 8 cm và diện tích xung quanh là 192π cm2:
Chiều cao của hình trụ là: h=\(\frac{S_{xp}}{2\pi R}=\frac{192\pi}{2\pi8}=12\)(cm).
Thể tích hình trụ là: V = πR2h = π . 82 . 12 = 768π (cm3).
Từ đó, ta có điền vào bảng như sau:
|
Hình |
Bán kính đáy (cm) |
Chiều cao (cm) |
Diện tích xung quanh (cm2) |
Thể tích (cm3) |
|
4 |
6 |
48π |
96π |
|
3 |
5 |
30π |
45π |
|
|
√ 5 |
10 |
20 √ 5 π |
50π |
|
|
8 |
12 |
192π |
768π |
Bài 10.2 trang 100
Cho hình chữ nhật ABCD có AB = 3 cm, BC = 4 cm. Quay hình chữ nhật quanh cạnh AB một vòng, ta được một hình trụ. Tính diện tích xung quanh và thể tích của hình trụ tạo thành.
Lời giải:
Khi quay hình chữ nhật quanh cạnh AB một vòng, ta được hình trụ có chiều cao h = 3 cm và bán kính R = 4 cm.
Diện tích xung quanh của hình trụ là:
Sxq = 2πRh = 2π . 4 . 3 = 24π (cm2).
Thể tích của hình trụ là:
V = Sđáy . h = πR2h = π . 42 . 3 = 48π (cm3).
Vậy hình trụ được tạo thành có diện tích xung quanh bằng 24π cm2 và thể tích bằng 48π cm3.
Bài 10.3 trang 100
Khi cho tam giác SOA vuông tại O quay quanh cạnh SO một vòng, ta được một hình nón. Biết OA = 8 cm, SA = 17 cm (H.10.14).
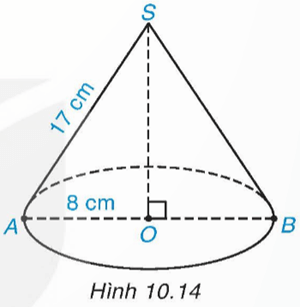
a) Tính diện tích xung quanh của hình nón.
b) Tính thể tích của hình nón.
Lời giải:
a) Diện tích xung quanh của hình nón là:
Sxq = π . OA . SA = π . 8 . 17 = 136π (cm2).
Vậy diện tích xung quanh của hình nón là 136π cm2.
b) Áp dụng định lí Pythagore vào tam giác SAO vuông tại O có:
SO2 + AO2 = SA2
Suy ra \(SO=\sqrt{SA^2-\ AO^2}\ =\sqrt{17^2-8^2}=15\)(cm).
Thể tích của hình nón là:
V=\(\frac{1}{3}\)π⋅AO2⋅SO=\(\frac{1}{3}\)π⋅82⋅15=320π(cm3).
Vậy thể tích của hình nón là 320π cm3.
Bài 10.4 trang 100
Một bóng đèn huỳnh quang có dạng hình trụ được đặt khít vào một hộp giấy cứng dạng hình hộp chữ nhật (H.10.15). Hộp giấy có chiều dài bằng 0,6 m, đáy là hình vuông cạnh 4 cm. Tính diện tích xung quanh và thể tích của bóng đèn (giả sử bề dày của hộp giấy không đáng kể).
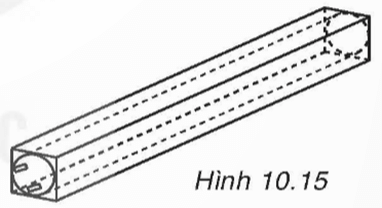
Lời giải:
Bóng đèn huỳnh quang đó có chiều cao bằng h = 0,6 m = 60 cm và đường kính đáy 4 cm nên bán kính đáy là R = 2 m.
Diện tích xung quanh của bóng đèn là:
Sxq = 2πRh = 2π . 60 . 2 = 240π (cm2).
Thể tích của bóng đèn là:
V = Sđáy . h = πR2h = π . 22 . 60 = 240π (cm3).
Vậy bóng đèn có diện tích xung quanh bằng 240π cm2 và thể tích bằng 240π cm3.
