Giải Toán 9 trang 103 tập 1 Kết nối tri thức
Giải Toán 9 trang 103 Tập 1
Giải Toán 9 trang 103 tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 1 trang 103.
Bài 5.20 Trang 103 Toán 9 Tập 1
Bạn Thanh cắt 4 hình tròn bằng giấy có bán kính lần lượt là 4 cm, 6 cm, 7 cm và 8 cm để dán trang trí trên một mảnh giấy, trên đó có vẽ trước hai đường thẳng a và b. Biết rằng a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 6 cm (nghĩa là mọi điểm trên đường thẳng b đều cách a một khoảng 6 cm). Hỏi nếu bạn Thanh dán sao cho tâm của cả 4 hình tròn đều nằm trên đường thẳng b thì hình nào đè lên đường thẳng a, hình nào không đè lên đường thẳng a?
Hướng dẫn giải:
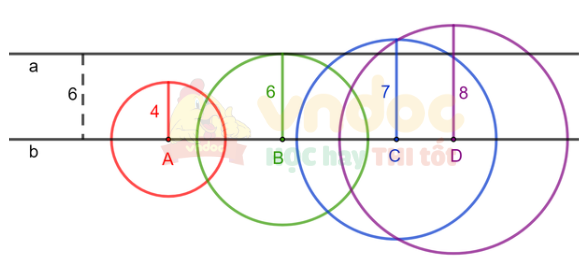
Giả sử bốn hình tròn có tâm là A, B, C, D. Khi đó ta có các đường tròn (A; 4 cm), (B; 6 cm), (C; 7 cm), (D; 8 cm)
- Đường tròn (A; 4 cm) có R1 = 4 cm < d = 6 cm nên không cắt lên đường thẳng a
- Đường tròn (B; 6 cm) có R2 = d = 6 cm nên tiếp xúc với đường thẳng a
- Đường tròn (C; 7 cm) có R3 = 7 cm > d = 6 cm nên cắt lên đường thẳng a
- Đường tròn (D; 8 cm) có R4 = 8 cm > d = 6 cm nên cắt lên đường thẳng a
Vậy các hình tròn có bán kính 4 cm và 6 cm không đè lên đt a; các đường tròn có bán kính 7 cm và 8 cm đè lên đường thẳng a.
Bài 5.21 Trang 103 Toán 9 Tập 1
Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A, Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O).
Hướng dẫn giải:
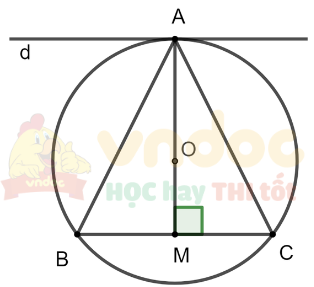
Giả sử d đi qua A và song song với BC
Ta có O là tâm đường tròn đi qua A, B, C nên O khác A và OB = OC
Mà AB = AC (tam giác ABC cân tại A)
Suy ra AO là đường trung trực của BC hay AO ⊥ BC
Mà d // BC, suy ra d ⊥ OA tại A
Vậy d là một tiếp tuyến của đường tròn (O) tại A.
Bài 5.22 Trang 103 Toán 9 Tập 1
Cho góc xOy với tia phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).
Hướng dẫn giải:
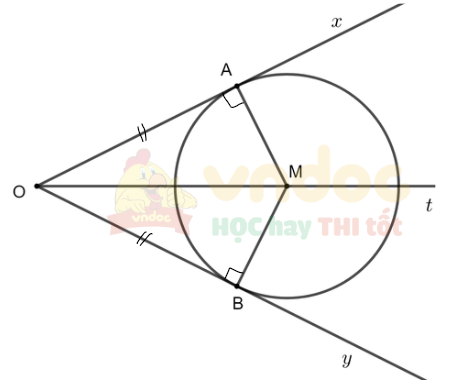
Xét tam giác OAM và tam giác OBM có:
OM chung
\(\widehat{AOM}=\widehat{BOM}\) (OM là tia phân giác của góc AOB)
OA = OB (gt)
Do đó, Δ OAM = Δ OBM (c . g . c)
Suy ra \(\widehat{OAM}=\widehat{OBM} =90^{\circ}\) (hai góc tương ứng)
Ta có AM = BM (Δ OAM = Δ OBM) nên B thuộc đường tròn tâm M, đường kính MA.
Ta có: MA ⊥ AO tại A
MB ⊥ BO tại A
Do đó OA và OB là hai tiếp tuyến cắt nhau của (O).
Bài 5.23 Trang 103 Toán 9 Tập 1
Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F.
a) Chứng minh rằng chu vi của tam giác SEF bằng SA + SB.
b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng SE = SF.
Hướng dẫn giải:
-----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 104 tập 1 Kết nối tri thức
Lời giải Toán 9 trang 103 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 16: Vị trí tương đối của đường thẳng và đường tròn, được VnDoc biên soạn và đăng tải!
