Toán 9 Kết nối tri thức Luyện tập chung trang 19
Giải Toán 9 Kết nối tri thức: Luyện tập chung trang 19 cung cấp lời giải chi tiết, khoa học cho các câu hỏi và bài tập thực hành trong Sách giáo khoa (Tập 2) từ trang 19 đến trang 20. Qua đó, các em không chỉ thành thạo kỹ năng giải các dạng toán phức hợp mà còn rèn luyện tư duy phân tích, cách trình bày bài giải logic và chính xác. Đây là nguồn tham khảo hữu ích giúp học sinh tự tin ôn tập, khắc phục những lỗi sai thường gặp và chuẩn bị nền tảng vững chắc cho các bài kiểm tra định kỳ. Mời quý thầy cô và các em cùng theo dõi, luyện tập để bứt phá điểm số môn Toán lớp 9.
Luyện tập chung trang 19 Kết nối tri thức tập 2
Giải Toán 9 trang 19
Bài 6.16 trang 19 Toán 9 Tập 2:
Biết rằng parabol ![]() đi qua điểm
đi qua điểm ![]() .
.
a) Tìm hệ số a và vẽ đồ thị của hàm số ![]() với a vừa tìm được.
với a vừa tìm được.
b) Tìm tung độ của điểm thuộc parabol có hoành độ ![]() .
.
c) Tìm các điểm thuộc parabol có tung độ ![]() .
.
Hướng dẫn giải:
a) Vì parabol ![]() đi qua điểm
đi qua điểm ![]() nên ta có:
nên ta có: ![]()
Suy ra, parabol cần tìm là: ![]() .
.
Vẽ đồ thị hàm số ![]() :
:
Lập bảng một số cặp giá trị tương ứng của x và y:
|
x |
–2 |
–1 |
0 |
1 |
2 |
|
y |
4√3 |
√3 |
0 |
√3 | 4√3 |
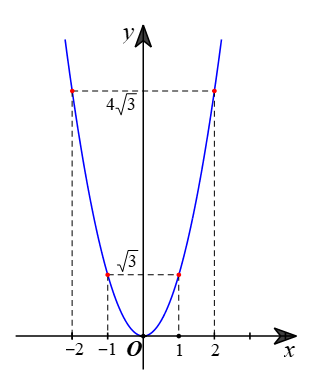
Biểu diễn các điểm ![]() trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số
trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số ![]() như hình vẽ.
như hình vẽ.
b) Thay ![]() vào hàm số
vào hàm số ![]() ta có:
ta có: ![]() . Vậy tung độ của điểm thuộc parabol có hoành độ
. Vậy tung độ của điểm thuộc parabol có hoành độ ![]() là
là ![]() .
.
c) Thay ![]() vào hàm số
vào hàm số ![]() ta có:
ta có: ![]() , suy ra
, suy ra ![]() hoặc
hoặc ![]() .
.
Vậy các điểm thuộc parabol có tung độ ![]() là
là ![]() .
.
Giải Toán 9 trang 20
Bài 6.17 trang 20 Toán 9 Tập 2:
Công thức ![]() được dùng để tính động năng của một vật có khối lượng m (kg) khi chuyển động với vận tốc v (m/s) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).
được dùng để tính động năng của một vật có khối lượng m (kg) khi chuyển động với vận tốc v (m/s) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).
a) Giả sử một quả bóng có khối lượng 2kg đang bay với vận tốc 6m/s. Tính động năng của quả bóng đó.
b) Giả sử động năng của quả bóng đang bay có khối lượng 1,5kg là 48J, hãy tính vận tốc bay của quả bóng đó.
Hướng dẫn giải:
a) Thay ![]() vào công thức
vào công thức ![]() ta có:
ta có: ![]()
Vậy động năng của quả bóng là 36J.
b) Thay ![]() vào công thức
vào công thức ![]() ta có:
ta có: ![]() , suy ra
, suy ra ![]() , do đó
, do đó ![]() (do
(do ![]() )
)
Vậy vận tốc bay của quả bóng là 8m/s khi động năng của quả bóng đang bay có khối lượng 1,5kg là 48J.
Chú ý khi giải: Vận tốc của vật trong chuyển động không âm, tức là ![]() .
.
Bài 6.18 trang 20 Toán 9 Tập 2:
Cho hình chóp tam giác đều có đáy là tam giác đều cạnh a (cm) và chiều cao 10 cm.
a) Tính diện tích đáy S của hình chóp theo a.
b) Từ kết quả câu a, tính thể tích V của hình chóp theo a và tính giá trị của V khi a = 4 cm.
c) Nếu độ dài cạnh đáy giảm đi hai lần thì thể tích hình chóp thay đổi như thế nào?
Hướng dẫn giải:
a) Ta có đáy hình chóp là tam giác đều cạnh a nên đường cao đồng thời là đường trung tuyến.
Suy ra đường cao là một cạnh của tam giác vuông có cạnh huyền là a và cạnh góc vuông còn lại là ![]()
Áp dụng định lí Pythagore, ta có đường cao của đáy là:

Diện tích đáy S của hình chóp là:
![]()
b) Khi a = 4 cm, ta có: ![]()
Thể tích V của hình chóp là:
![]()
c) Độ dài cạnh đáy mới là ![]()
Chiều cao đáy mới là:
hmới = ![]()
![]()
Diện tích đáy mới là:
Smới = ![]() =
= ![]() .Scũ.
.Scũ.
Suy ra Vmới = ![]() .Smới.h =
.Smới.h = ![]() .Scũ.h =
.Scũ.h = ![]() .Vcũ
.Vcũ
Vậy nếu độ dài cạnh đáy giảm đi hai lần thì thể tích hình chóp giảm đi 4 lần.
Bài 6.19 trang 20 Toán 9 Tập 2:
Sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn, giải các phương trình sau:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() ;
;
d) ![]() .
.
Hướng dẫn giải:
a) Ta có: ![]() nên phương trình có hai nghiệm phân biệt:
nên phương trình có hai nghiệm phân biệt: ![]()
b) Ta có: ![]() nên phương trình có hai nghiệm phân biệt:
nên phương trình có hai nghiệm phân biệt: ![]()
c) Ta có: ![]() nên phương trình vô nghiệm.
nên phương trình vô nghiệm.
d) Ta có: ![]() nên phương trình có nghiệm kép
nên phương trình có nghiệm kép ![]() .
.
Bài 6.21 trang 20 Toán 9 Tập 2:
Từ một tấm tôn hình vuông, người ta cắt bỏ bốn hình vuông có độ dài cạnh 8 cm ở bốn góc, sau đó gập thành một chiếc thùng có dạng hình hộp chữ nhật không có nắp và có thể tích là 200 cm3. Tính độ dài cạnh của tấm tôn hình vuông ban đầu.
Hướng dẫn giải
Gọi độ dài cạnh của tấm tôn ban đầu là x (cm) (x > 16).
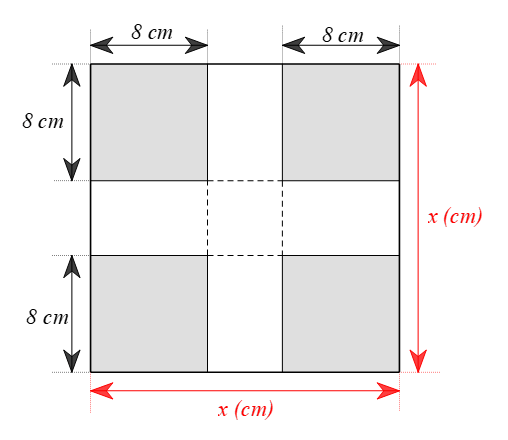
Sau khi người ta cắt bỏ bốn hình vuông có độ dài cạnh 8 cm ở bốn góc, sau đó gập thành một chiếc thùng có dạng hình hộp chữ nhật thì:
⦁ cạnh đáy (đáy hình vuông) là: x – 8.2 = x – 16 (cm);
⦁ chiều cao là: 8 (cm).
Thể tích hình hộp chữ nhật: 8(x – 16)2 (cm3).
Theo đề bài ta có phương trình: 8(x – 16)2 = 200.
Giải phương trình:
8(x – 16)2 = 200
(x – 16)2 = 25
x – 16 = 5 hoặc x – 16 = –5
x = 21 hoặc x = 11.
Ta thấy chỉ có giá trị x = 21 thỏa mãn điều kiện x > 16.
Vậy độ dài cạnh của tấm tôn ban đầu là 21 cm.
Bài 6.22 trang 20 Toán 9 Tập 2:
Giả sử doanh thu (nghìn đồng) của một cửa hàng bán phở trong một ngày có thể mô hình hoá bằng công thức R(x) = x(220 – 4x) với 30 ≤ x ≤ 50, trong đó x (nghìn đồng) là giá tiền của một bát phở. Nếu muốn doanh thu của cửa hàng đạt 3 triệu đồng thì giá bán của mỗi bát phở phải là bao nhiêu?
Hướng dẫn giải
Để doanh thu cửa hàng đạt 3 triệu đồng thì ![]()
hay ![]()
Ta có: ![]() nên phương trình có hai nghiệm phân biệt
nên phương trình có hai nghiệm phân biệt
![]()
Vậy để doanh thu cửa hàng đạt 3 triệu đồng thì giá bán của mỗi bát phở phải là 30 000 đồng.








