VnDoc.com

Giải Toán 9 trang 90 tập 1 Kết nối tri thức

Bài trước

Bài sau

Giải Toán 9 trang 90 Tập 1

Luyện tập 2 Trang 90 Toán 9 Tập 1
Bài 5.5 Trang 90 Toán 9 Tập 1
Bài 5.6 Trang 90 Toán 9 Tập 1
Bài 5.7 Trang 90 Toán 9 Tập 1
Bài 5.8 Trang 90 Toán 9 Tập 1

Giải Toán 9 trang 90 tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 1 trang 90.

Luyện tập 2 Trang 90 Toán 9 Tập 1

Cho điểm C nằm trên đường tròn (O). Đường trung trực của đoạn OC cắt (O) tại A và B. Tính số đo của các cung $\overset \frown {ACB}$ $\overset \frown {ACB}$ và $\overset \frown { ABC}$ $\overset \frown { ABC}$.

Hướng dẫn giải:

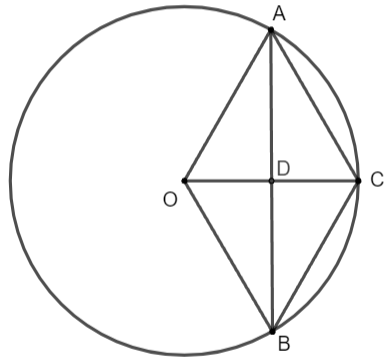
Gọi D là trung điểm của OC.

Xét tam giác vuông OAD có OD = 1/2 OC = 1/2 OA

$\cos \widehat{AOD}=\frac{OD}{OA}=\frac{1}{2}$ $\cos \widehat{AOD}=\frac{OD}{OA}=\frac{1}{2}$

Suy ra $\widehat{AOC} =\widehat{BOC} =60^{\circ}$ $\widehat{AOC} =\widehat{BOC} =60^{\circ}$

Do đó $\widehat{AOB} =2\widehat{AOC} =120^{\circ}$ $\widehat{AOB} =2\widehat{AOC} =120^{\circ}$

Vậy sđ $\overset \frown {ACB}$ $\overset \frown {ACB}$ = 120^o.

Ta có: sđ $\overset \frown {ACB}$ $\overset \frown {ACB}$ = 360^o - 60^o = 300^o.

Bài 5.5 Trang 90 Toán 9 Tập 1

Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó. Chứng minh rằng khoảng cách từ M đến AB không lớn hơn $\frac{AB}{2}$ $\frac{AB}{2}$.

Hướng dẫn giải:

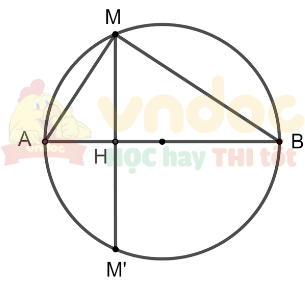
Kẻ MH ⊥ AB (M thuộc AB)

Gọi M' đối xứng với M qua AB và cắt AB tại H.

Khi đó H là trung điểm của MM'

Mặt khác: Do AB là trục đối xứng của đường tròn nên M' thuộc đường tròn đó.

Vậy MM' là một dây của đường tròn.

Do đó MM' ≤ AB hay 2MH ≤ AB

Vậy $MM'\le\frac{AB}{2}$.

Bài 5.6 Trang 90 Toán 9 Tập 1

Cho đường tròn (O; 5 cm) và AB là một dây bất kì của đường tròn đó. Biết AB = 6 cm.

a) Tính khoảng cách từ O đến đường thẳng AB.

b) Tính tan α nếu góc ở tâm chắn cung AB bằng 2α.

Hướng dẫn giải:

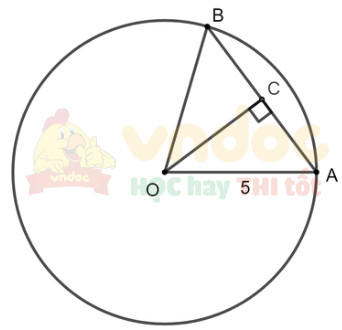
a) Gọi C là trung điểm của AB nên AC = CB = 3 cm

Tam giác OAB cân tại O (OA = OB) có OC là đường trung tuyến

Suy ra OC cũng là đường cao hay OC ⊥ AB

Vậy khoảng cách từ O đến đường thẳng AB là OC

Xét tam giác OAC vuông tại C có:

OC² + AC² = OA² (định lý Pythagore)

Suy ra OC² = OA² - AC² = 5² - 3² = 16

Vậy OC = 4 cm.

b) Tam giác cân OAB có OC là đường trung tuyến nên OC cũng là đường phân giác

Do đó $\widehat {AOC} = \widehat {BOC} =\frac{\widehat {AOB}}{ 2} =\alpha$ $\widehat {AOC} = \widehat {BOC} =\frac{\widehat {AOB}}{ 2} =\alpha$

Xét tam giác OAC vuông tại C ta có:

$\tan \alpha =\tan \widehat{AOC}=\frac{AC}{OC} =\frac{3}{4}$ $\tan \alpha =\tan \widehat{AOC}=\frac{AC}{OC} =\frac{3}{4}$

Bài 5.7 Trang 90 Toán 9 Tập 1

Tâm O của một đường tròn cách dây AB của nó một khoảng 3 cm. Tính bán kính của đường tròn (O), biết rằng dây cung nhỏ AB có số đo bằng 100^o (làm tròn kết quả đến hàng phần mười).

Hướng dẫn giải:

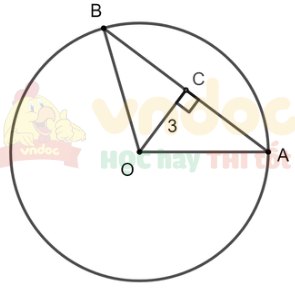
Do cung nhỏ AB có số đo bằng 100^o nên $\widehat {AOB} = \text{sđ }\overset\frown{AB}=100{}^\circ$ $\widehat {AOB} = \text{sđ }\overset\frown{AB}=100{}^\circ$

Gọi C là trung điểm của AB.

Tam giác OAB cân tại O (OA = OB) có OC là đường trung tuyến

Suy ra OC cũng là đường cao và là đường phân giác

Do đó OC ⊥ AB và $\widehat {AOC} =\widehat {BOC}= \frac{{100^\circ }}{2} = 50^\circ$ $\widehat {AOC} =\widehat {BOC}= \frac{{100^\circ }}{2} = 50^\circ$

Xét tam giác OAC vuông tại C có:

$\cos \widehat {AOC} = \frac{{OC}}{{OA}}$ $\cos \widehat {AOC} = \frac{{OC}}{{OA}}$

$\Rightarrow OA = \frac{{OC}}{{\cos \widehat {AOC}}} = \frac{3}{{\cos 50^\circ }} \approx 4,67$ $\Rightarrow OA = \frac{{OC}}{{\cos \widehat {AOC}}} = \frac{3}{{\cos 50^\circ }} \approx 4,67$ cm