Giải Toán 9 trang 73 tập 1 Kết nối tri thức
Giải Toán 9 trang 73 Tập 1
Giải Toán 9 trang 73 tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 1 trang 73.
Bài 4.1 Trang 73 Toán 9 Tập 1
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, côsin, tang, côtang của các góc nhọn B và C khi biết:
a) AB = 8 cm, BC = 17 cm;
b) AC = 0,9 cm, AB = 1,2 cm.
Hướng dẫn giải:
a) Xét tam giác ABC vuông tại A, theo định lí Pythagore, ta có:
BC2 = AB2 + AC2
⇒ AC2 = BC2 - AB2 = 172 - 82 = 225
⇒ AC = 15 cm
Theo định nghĩa của tỉ số lượng giác sin, côsin, tang, côtang, ta có:
\(\sin B = \cos C=\frac{AC}{BC}=\frac{15}{17}\)
\(\cos B = \sin C=\frac{AB}{BC}=\frac{8}{17}\)
\(\tan B = \cot C=\frac{AC}{AB}=\frac{15}{8}\)
\(\cot B = \tan C=\frac{AB}{AC}=\frac{8}{15}\)
b) Xét tam giác ABC vuông tại A, theo định lí Pythagore, ta có:
BC2 = AB2 + AC2 = 0,92 + 1,22 = 2,25
⇒ BC = 1,5 cm
Theo định nghĩa của tỉ số lượng giác sin, côsin, tang, côtang, ta có:
\(\sin B = \cos C=\frac{AC}{BC}=\frac{1,2}{1,5} =\frac{4}{5}\)
\(\cos B = \sin C=\frac{AB}{BC}=\frac{0,9}{1,5} =\frac{3}{ 5}\)
\(\tan B = \cot C=\frac{AC}{AB}=\frac{1,2}{0,9} =\frac{4}{3}\)
\(\cot B = \tan C=\frac{AB}{AC}=\frac{0,9}{1,2}=\frac{3}{4}\)
Bài 4.2 Trang 73 Toán 9 Tập 1
Cho tam giác vuông có một góc nhọn 60° và cạnh kề với góc 60° bằng 3 cm. Hãy tính cạnh đối của góc này.
Hướng dẫn giải:
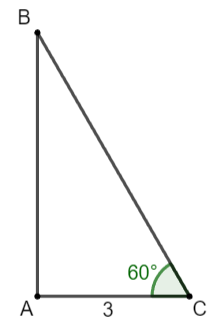
Xét tam giác ABC vuông tại A:
Theo định nghĩa của tỉ số lượng giác tan, ta có:
\(\tan60^o=\frac{AB}{AC}=\frac{AB}{3}\)
⇒ AB = 3 . tan 60o = \(3\sqrt{3}\) (cm)
Bài 4.3 Trang 73 Toán 9 Tập 1
Cho tam giác vuông có một góc nhọn bằng 30° và cạnh đối với góc này bằng 5 cm. Tính độ dài cạnh huyền của tam giác.
Hướng dẫn giải:
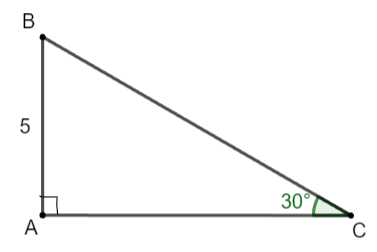
Xét tam giác ABC vuông tại A:
Theo định nghĩa của tỉ số lượng giác sin, ta có:
\(\sin30^o=\frac{AB}{BC}=\frac{5}{BC}\)
⇒ \(BC=\frac{5}{\sin30^o}=10\) (cm)
Bài 4.4 Trang 73 Toán 9 Tập 1
Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và \(\sqrt{3}\). Tính góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác trang 69).
Hướng dẫn giải:
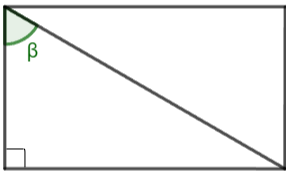
Góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật là góc β
Theo định nghĩa của tỉ số lượng giác tan, ta có:
\(\tan \beta=\frac{3 }{ \sqrt{3} } =\sqrt{3}\) ⇒ β = 60o.
Bài 4.5 Trang 73 Toán 9 Tập 1
a) Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45°:
sin 55o, cos 62o, tan 57o, cot 64o.
b) Tính \(\frac{\tan25^o}{\cot65^o}\), tan 34o − cot 56o.
Hướng dẫn giải:
a) Ta có:
sin 55o = cos (90o – 55o) = cos 35o
cos 62o = sin (90o – 62o) = sin 28o
tan 57o = cot (90o – 57o) = cot 33o
cot 64o = tan (90o – 64o) = tan 26o.
b) Ta có:
\(\frac{\tan25^o}{\cot65^o}=\frac{\cot65^o}{\cot65^o}=1\)
tan 34o − cot 56o = cot 56o − cot 56o = 0
Bài 4.6 Trang 73 Toán 9 Tập 1
Dùng MTCT, tính (làm tròn đến chữ số thập phân thứ ba):
a) sin 40o12'
b) cos 52o54'
c) tan 63o36'
d) cot 35o20'
Hướng dẫn giải:
Sử dụng MTCT, ta được:
a) sin 40o12' ≈ 0,645
b) cos 52o54' ≈ 0,603
c) tan 63o36' ≈ 2,014
d) cot 35o20' ≈ 1,411
Bài 4.7 Trang 73 Toán 9 Tập 1
Dùng MTCT, tìm số đo của góc nhọn x (làm tròn đến phút), biết rằng:
a) sin x = 0,2368
b) cos x = 0,6224
c) tan x = 1,236
d) cot x = 2,154
Hướng dẫn giải:
Sử dụng MTCT, ta được:
a) sin x = 0,2368 ⇒ x ≈ 13o42'
b) cos x = 0,6224 ⇒ x ≈ 51o3'
c) tan x = 1,236 ⇒ x ≈ 51o1'
d) cot x = 2,154 ⇒ x ≈ 24o54'
-----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 74 tập 1 Kết nối tri thức
Toán 9 Kết nối tri thức Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng
Lời giải Toán 9 trang 73 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 11: Tỉ số lượng giác của góc nhọn, được VnDoc biên soạn và đăng tải!
