Giải Toán 9 trang 81 tập 1 Cánh diều
Giải Toán 9 trang 81 Tập 1
- Bài 1 trang 81 Toán 9 Tập 1 Cánh diều
- Bài 2 trang 81 Toán 9 Tập 1 Cánh diều
- Bài 3 trang 81 Toán 9 Tập 1 Cánh diều
- Bài 4 trang 81 Toán 9 Tập 1 Cánh diều
- Bài 5 trang 81 Toán 9 Tập 1 Cánh diều
- Bài 6 trang 81 Toán 9 Tập 1 Cánh diều
- Bài 7 trang 81 Toán 9 Tập 1 Cánh diều
- Bài 8 trang 81 Toán 9 Tập 1 Cánh diều
Giải Toán 9 trang 81 Tập 1 Cánh diều hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Cánh diều tập 1 trang 81.
Bài 1 trang 81 Toán 9 Tập 1 Cánh diều
Cho tam giác ABC vuông tại A có AC = 4 cm, BC = 6 cm. Tính các tỉ số lượng giác của góc B.
Hướng dẫn giải
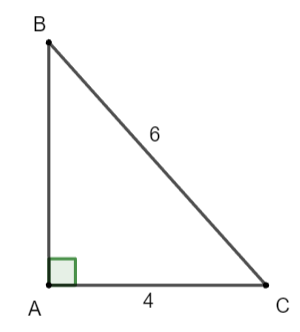
Áp dụng định lí Pythagore trong tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
Suy ra AB2 = BC2 − AC2 = 62 - 42 = 20
Do đó ![]() \(AB=2\sqrt{5}\) cm
\(AB=2\sqrt{5}\) cm
Ta có: ![]() \(\sin B=\frac{AC}{BC}=\frac{4}{6} =\frac{2}{3}\)
\(\sin B=\frac{AC}{BC}=\frac{4}{6} =\frac{2}{3}\)
![]() \(\cos B=\frac{AB}{BC}=\frac{2\sqrt{5} }{6} =\frac{\sqrt{5}}{3}\)
\(\cos B=\frac{AB}{BC}=\frac{2\sqrt{5} }{6} =\frac{\sqrt{5}}{3}\)
![]() \(\tan B=\frac{AC}{AB}=\frac{4}{2\sqrt{5} } =\frac{2}{ \sqrt{5} }\)
\(\tan B=\frac{AC}{AB}=\frac{4}{2\sqrt{5} } =\frac{2}{ \sqrt{5} }\)
![]() \(\cot B=\frac{AB}{AC}=\frac{2\sqrt{5} }{4} = \frac{ \sqrt{5} }{2}\)
\(\cot B=\frac{AB}{AC}=\frac{2\sqrt{5} }{4} = \frac{ \sqrt{5} }{2}\)
Bài 2 trang 81 Toán 9 Tập 1 Cánh diều
Cho tam giác ABC vuông tại A có AB = 2 cm, AC = 3 cm. Tính các tỉ số lượng giác của góc C.
Hướng dẫn giải
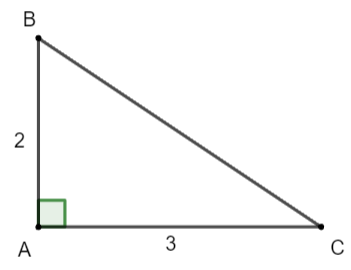
Áp dụng định lí Pythagore trong tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2 = 22 + 32 = 13
Do đó ![]() \(BC= \sqrt{13}\) cm
\(BC= \sqrt{13}\) cm
Ta có: ![]() \(\sin C=\frac{AB}{BC}=\frac{2}{\sqrt{5} }\)
\(\sin C=\frac{AB}{BC}=\frac{2}{\sqrt{5} }\)
![]() \(\cos C=\frac{AC}{BC}=\frac{3 }{\sqrt{5}}\)
\(\cos C=\frac{AC}{BC}=\frac{3 }{\sqrt{5}}\)
![]() \(\tan C=\frac{AB}{AC}=\frac{2}{3}\)
\(\tan C=\frac{AB}{AC}=\frac{2}{3}\)
![]() \(\cot C=\frac{AC}{AB}=\frac{3 }{2}\)
\(\cot C=\frac{AC}{AB}=\frac{3 }{2}\)
Bài 3 trang 81 Toán 9 Tập 1 Cánh diều
Cho tam giác MNP có MN = 5 cm, MP = 12 cm, NP = 13 cm. Chứng minh tam giác MNP vuông tại M. Từ đó, tính các tỉ số lượng giác của góc N.
Hướng dẫn giải
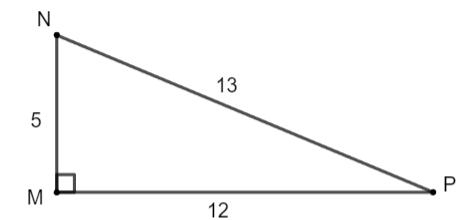
Ta có: 132 = 52 + 122 = 169 hay NP2 = MN2 + MP2.
Xét tam giác MNP có NP2 = MN2 + MP2 nên tam giác MNP vuông tại M (định lí Pythagore đảo).
Khi đó: ![]() \(\sin N=\frac{MP}{NP}=\frac{12}{13 }\)
\(\sin N=\frac{MP}{NP}=\frac{12}{13 }\)
![]() \(\cos N=\frac{MN}{NP}=\frac{5}{13}\)
\(\cos N=\frac{MN}{NP}=\frac{5}{13}\)
![]() \(\tan N=\frac{MP}{MN}=\frac{12}{5}\)
\(\tan N=\frac{MP}{MN}=\frac{12}{5}\)
![]() \(\cot N=\frac{MN}{MP}=\frac{5}{12}\)
\(\cot N=\frac{MN}{MP}=\frac{5}{12}\)
Bài 4 trang 81 Toán 9 Tập 1 Cánh diều
Mỗi tỉ số lượng giác sau đây bằng tỉ số lượng giác nào của góc 63o? Vì sao?
a) sin 27o
b) cos 27o
c) tan 27o
d) cot 27o
Hướng dẫn giải
Do 27o và 63o là hai góc phụ nhau, ta có:
a) sin 27o = cos63o
b) cos 27o = sin 63o
c) tan 27o = cot 63o
d) cot 27o = tan 63o
Bài 5 trang 81 Toán 9 Tập 1 Cánh diều
Sử dụng máy tính cầm tay để tính các tỉ số lượng giác của mỗi góc sau (làm tròn kết quả đến hàng phần trăm):
a) 41o
b) 28o 35'
c) 70o 27' 46''
Hướng dẫn giải
a) sin 41o ≈ 0,66
cos 41o ≈ 0,75
tan 41o ≈ 0,87
cot 41o ≈ 1,15
b) sin 28o 35' ≈ 0,48
cos 28o 35' ≈ 0,88
tan 28o 35' ≈ 0,54
cot 28o 35' ≈ 1,84
c) sin 70o 27' 46'' ≈ 0,94
cos 70o 27' 46'' ≈ 0,33
tan 70o 27' 46'' ≈ 2,82
cot 70o 27' 46'' ≈ 0,35
Bài 6 trang 81 Toán 9 Tập 1 Cánh diều
Sử dụng tỉ số lượng giác của hai góc phụ nhau, tính giác trị biểu thức:
A = sin 25o + cos 25o – sin 65o – cos 65o.
Hướng dẫn giải
Ta có: A = sin 25o + cos 25o – sin 65o – cos 65o
= cos 65o + cos 25o – cos 25o – cos 65o
= 0
Bài 7 trang 81 Toán 9 Tập 1 Cánh diều
Cho góc nhọn α. Biết rằng, tam giác ABC vuông tại A có ![]() \(\widehat{B} = \alpha\)
\(\widehat{B} = \alpha\)
a) Biểu diễn các tỉ số lượng giác của góc nhọn α theo AB, BC, CA
b) Chứng minh: sin2 α + cos2 α = 1; ![]() \(\tan\alpha=\frac{\sin\alpha}{\cos\alpha};\ \cot\alpha=\frac{\cos\alpha}{\sin\alpha}\); tan α . cot α = 1
\(\tan\alpha=\frac{\sin\alpha}{\cos\alpha};\ \cot\alpha=\frac{\cos\alpha}{\sin\alpha}\); tan α . cot α = 1
Từ đó, tính giá trị của biểu thức:
S = sin2 35o + cos2 35o; T = tan 61o . cot 61o.
Hướng dẫn giải
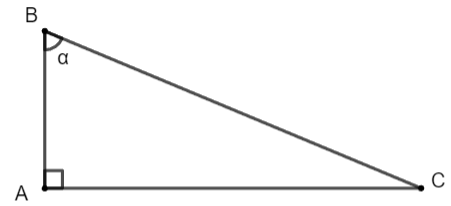
a) Xét tam giác ABC vuông tại A, ta có:
AB2 + AC2 = BC2 (định lí Pythagore)
![]() \(\sin \alpha=\frac{AC}{BC}\);
\(\sin \alpha=\frac{AC}{BC}\); ![]() \(\cos \alpha=\frac{AB}{BC}\)
\(\cos \alpha=\frac{AB}{BC}\)
![]() \(\tan \alpha=\frac{AC}{AB}\);
\(\tan \alpha=\frac{AC}{AB}\); ![]() \(\cot \alpha=\frac{AB}{AC}\)
\(\cot \alpha=\frac{AB}{AC}\)
b) Từ câu a, ta có:
![]() \(\sin^2\alpha+\cos^2\alpha=\frac{AB^2}{BC^2}+\frac{AC^2}{BC^2}=\frac{BC^2}{BC^2}=1\)
\(\sin^2\alpha+\cos^2\alpha=\frac{AB^2}{BC^2}+\frac{AC^2}{BC^2}=\frac{BC^2}{BC^2}=1\)
![]() \(\tan\alpha=\frac{AC}{AB}=\frac{AC}{BC}. \frac{BC}{AB}=\frac{AC}{BC}:\frac{AB}{BC}=\frac{\sin\alpha}{\cos\alpha}\)
\(\tan\alpha=\frac{AC}{AB}=\frac{AC}{BC}. \frac{BC}{AB}=\frac{AC}{BC}:\frac{AB}{BC}=\frac{\sin\alpha}{\cos\alpha}\)
![]() \(\cot\alpha=\frac{AB}{AC}=\frac{AB}{BC}. \frac{BC}{AC}=\frac{AB}{BC}:\frac{AC}{BC}=\frac{\cos\alpha}{\sin\alpha}\)
\(\cot\alpha=\frac{AB}{AC}=\frac{AB}{BC}. \frac{BC}{AC}=\frac{AB}{BC}:\frac{AC}{BC}=\frac{\cos\alpha}{\sin\alpha}\)
![]() \(\tan\alpha\ .\ \cot\alpha=\frac{\sin\alpha}{\cos\alpha}\ .\ \frac{\cos\alpha}{\sin\alpha}=1\)
\(\tan\alpha\ .\ \cot\alpha=\frac{\sin\alpha}{\cos\alpha}\ .\ \frac{\cos\alpha}{\sin\alpha}=1\)
Vậy: S = sin2 35o + cos2 35o = 1
T = tan 61o . cot 61o = 1
Bài 8 trang 81 Toán 9 Tập 1 Cánh diều
Hình 10 mô tả tia nắng mặt trời dọc theo AB tạo với phương nằm ngang trên mặt đất một góc ![]() \(\alpha =\widehat {ABH}\). Sử dụng máy tính cầm tay, tính số đo góc α (làm tròn kết quả đến hàng đơn vị của độ) biết AH = 2 m, BH = 5 m.
\(\alpha =\widehat {ABH}\). Sử dụng máy tính cầm tay, tính số đo góc α (làm tròn kết quả đến hàng đơn vị của độ) biết AH = 2 m, BH = 5 m.
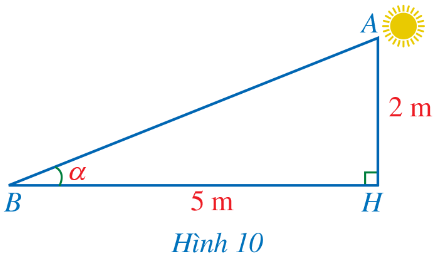
Hướng dẫn giải
Xét tam giác ABH vuông tại H, ta có:
![]() \(\tan\alpha=\tan B=\frac{HA}{HB}=\frac{2}{5}=0,4\)
\(\tan\alpha=\tan B=\frac{HA}{HB}=\frac{2}{5}=0,4\)
Vậy α ≈ 22o.
-----------------------------------------------
---> Trang tiếp theo: Giải Toán 9 trang 82 tập 1 Cánh diều
Lời giải Toán 9 trang 81 Tập 1 Cánh diều với các câu hỏi nằm trong Bài 1: Tỉ số lượng giác của góc nhọn, được VnDoc biên soạn và đăng tải!









