Toán 9 Cánh diều Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

Giải Toán 9 Cánh diều Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Cánh diều tập 1 trang 61, 62, 63, 64, 65, 66.

Giải Toán 9 trang 61

Hoạt động 1 trang 61 SGK Toán 9 Cánh diều

Cửa hàng điện máy trưng bày một chiếc ti vi màn hình phẳng 55in, tức là độ dài đường chéo của màn hình tivi bằng 55in (1in = 2,54cm). Gọi \(x\left( {in} \right)\) là chiều rộng của màn hìn tivi (Hình 5). Viết công thức tính chiều dài của màn hình ti vi theo \(x\).

Hướng dẫn giải

Chiều dài của màn hình ti vi là: \(\sqrt {{{55}^2} - {x^2}}\).

Giải Toán 9 trang 62

Luyện tập 1 trang 62 SGK Toán 9 Cánh diều

Mỗi biểu thức sau có phải là một căn thức bậc hai hay không?

a. \(\sqrt {2x - 5}\).

b. \(\sqrt {\frac{1}{x}}\).

c. \(\frac{1}{{x + 1}}\).

Hướng dẫn giải

a. Biểu thức \(\sqrt {2x - 5}\) là một căn thức bậc hai vì \(2x - 5\) là một biểu thức đại số.

b. Biểu thức \(\sqrt {\frac{1}{x}}\) là một căn thức bậc hai vì \(\frac{1}{x}\) là một biểu thức đại số.

c. Biểu thức \(\frac{1}{{x + 1}}\) không là một căn thức bậc hai.

Luyện tập 2 trang 62 SGK Toán 9 Cánh diều

Tính giá trị của \(\sqrt {2{x^2} + 1}\) tại:

a. \(x = 2\);

b. \(x = - \sqrt {12}\).

Hướng dẫn giải

a. Thay \(x = 2\) vào biểu thức, ta được:

\(\sqrt {{{2.2}^2} + 1} = \sqrt 9 = 3\).

b. Thay \(x = - \sqrt {12}\) vào biểu thức, ta được:

\(\sqrt {2.{{\left( { - \sqrt {12} } \right)}^2} + 1} = \sqrt {25} = 5\).

Hoạt động 2 trang 62 SGK Toán 9 Cánh diều

Cho căn thức bậc hai \(\sqrt {x - 1}\). Biểu thức đó có xác định hay không tại mỗi giá trị sau?

a. \(x = 0\).

b. \(x = 1\).

c. \(x = 2\).

Hướng dẫn giải

a. Thay \(x = 0\) vào biểu thức, ta được: \(\sqrt {0 - 1} = \sqrt { - 1}\).

Vậy biểu thức đã cho không xác định.

b. Thay \(x = 1\) vào biểu thức, ta được: \(\sqrt {1 - 1} = \sqrt 0 = 0\).

Vậy biểu thức đã cho xác định.

c. Thay \(x = 2\) vào biểu thức, ta được: \(\sqrt {2 - 1} = \sqrt 1 = 1\).

Vậy biểu thức đã cho xác định.

Giải Toán 9 trang 63

Luyện tập 3 trang 63 SGK Toán 9 Cánh diều

Tìm điều kiện xác định cho mỗi căn thức bậc hai sau:

a. \(\sqrt {x + 1}\);

b. \(\sqrt {{x^2} + 1}\).

Hướng dẫn giải

a. \(\sqrt {x + 1}\) xác định khi \(x + 1 \ge 0\) hay \(x \ge - 1\).

b. \(\sqrt {{x^2} + 1}\) xác định khi \({x^2} + 1 \ge 0\) (đúng \(\forall x \in \mathbb{R}\)).

Giải Toán 9 trang 65

Bài 1 trang 65 Toán 9 Tập 1 Cánh diều

Tính giá trị của mỗi căn thức bậc hai sau:

a. \(\sqrt[{}]{{17 - {x^2}}}\) tại x = 1; x = - 3; x = \(2\sqrt[{}]{2};\)

b.\(\sqrt[{}]{{{x^2} + x + 1}}\) tại x = 0;x = - 1; x = - 7.

Hướng dẫn giải:

a. Thay x = 1 vào biểu thức, ta được: \(\sqrt {17 - {1^2}} = \sqrt {17 - 1} = \sqrt {16} = 4.\)

Thay x = - 3 vào biểu thức, ta được: \(\sqrt {17 - {{\left( { - 3} \right)}^2}} = \sqrt {17 - 9} = \sqrt 8 .\)

Thay\(x = 2\sqrt 2\) vào biểu thức, ta được: \(\sqrt {17 - {{\left( {2\sqrt 2 } \right)}^2}} = \sqrt {17 - 8} = \sqrt 9 = 3.\)

b. Thay x = 0 vào biểu thức, ta được: \(\sqrt {{0^2} + 0 + 1} = \sqrt 1 = 1.\)

Thay x = - 1 vào biểu thức, ta được: \(\sqrt {{{\left( { - 1} \right)}^2} + \left( { - 1} \right) + 1} = \sqrt 1 = 1.\)

Thay x = - 7 vào biểu thức, ta được: \(\sqrt {{{\left( { - 7} \right)}^2} + \left( { - 7} \right) + 1} = \sqrt {49 - 7 + 1} = \sqrt {43} .\)

Căn thức bậc hai và căn thức bậc ba của biểu thức đại số trang 65 Toán 9 Tập 1 Cánh diều

Tìm điều kiện xác định cho mỗi căn thức bậc hai sau:

a. \(\sqrt[{}]{{x - 6}}\)

b.\(\sqrt[{}]{{17 - x}}\)

c.\(\sqrt[{}]{{\frac{1}{x}}}\)

Hướng dẫn giải:

a. \(\sqrt {x - 6}\)xác định khi \(x - 6 \ge 0\) hay \(x \ge 6.\)

b.\(\sqrt {17 - x}\) xác định khi 1\(7 - x \ge 0\) hay \(x \le 17.\)

c. \(\sqrt {\frac{1}{x}}\)xác định khi \(\frac{1}{x} \ge 0\) và \(x \ne 0\) hay x > 0.

Bài 3 trang 65 Toán 9 Tập 1 Cánh diều

Tính giá trị của mỗi căn thức bậc ba sau:

a. \(\sqrt[3]{{2x - 7}}\) tại x = - 10; x = 7,5; x = - 0,5

b. \(\sqrt[3]{{{x^2} + 4}}\) tại x = 0; x = 2 ;\(x = \sqrt[{}]{{23}}.\)

Hướng dẫn giải:

a. Thay x = - 10 vào biểu thức, ta được:

Thay x = 7,5 vào biểu thức, ta được: \(\sqrt[3]{{2.7,5 - 7}} = \sqrt[3]{{15 - 7}} = \sqrt[3]{8} = 2.\)

Thay x = - 0,5 vào biểu thức, ta được: \(\sqrt[3]{{2.\left( { - 0,5} \right) - 7}} = \sqrt[3]{{ - 1 - 7}} = \sqrt[3]{{ - 8}} = - 2.\)

b. Thay x = 0 vào biểu thức, ta được: \(\sqrt[3]{{{0^2} + 4}} = \sqrt[3]{4}.\)

Thay x = 2 vào biểu thức, ta được:\(\sqrt[3]{{{2^2} + 4}} = \sqrt[3]{{4 + 4}} = \sqrt[3]{8} = 2.\)

Thay \(x = \sqrt[{}]{{23}}\) vào biểu thức, ta được: \(\sqrt[3]{{{{\left( {\sqrt[{}]{{23}}} \right)}^2} + 4}} = \sqrt[3]{{23 + 4}} = \sqrt[3]{{27}} = 3.\)

Giải Toán 9 trang 66

Bài 4 trang 66 Toán 9 Tập 1 Cánh diều

Tìm điều kiện xác định cho mỗi căn thức bậc ba sau:

a. \(\sqrt[3]{{3x + 2}}\)

b. \(\sqrt[3]{{{x^3} - 1}}\)

c. \(\sqrt[3]{{\frac{1}{{2 - x}}}}\)

Hướng dẫn giải:

a. \(\sqrt[3]{{3x + 2}}\) xác định với mọi số thực x vì 3x + 2 xác định với mọi số thực x.

b. \(\sqrt[3]{{{x^3} - 1}}\) xác định với mọi số thực x vì \({x^3}\) - 1 xác định với mọi số thực x.

c. \(\sqrt[3]{{\frac{1}{{2 - x}}}}\) xác định với \(x \ne 2\) vì \(\frac{1}{{2 - x}}\) xác định với x \ne 2.

Bài 5 trang 66 Toán 9 Tập 1 Cánh diều

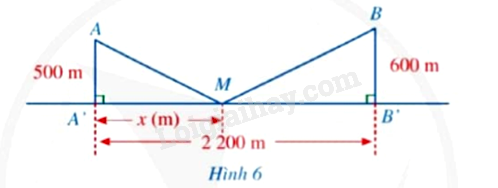
Có hai xã A, B cùng ở một bên bờ sông Lam, khoảng cách từ hai xác đó đến bờ sông lần lượt là AA' = 500m,BB' = 600m và người ta đo dược A'B' = 2200m. Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Giả sử vị trí của trạm cung cấp nước sạch đó là điểm M trên đoạn A'B' với MA' = x\left( m \right), 0 < x < 2200 (minh họa ở Hình 6).

a. Hãy tính tổng khoảng cách MA + MB theo x.

b. Tính tổng khoảng cách MA + MB khi x = 1200 (làm tròn kết quả đến hàng đơn vị của mét).

Hướng dẫn giải:

a. Ta có: MB = 2200 - x

Áp dụng định lý Py – ta – go vào tam giác MAA’ ta có:

\(\begin{array}{l}M{A^2} = MA{'^2} + AA{'^2}\\M{A^2} = {x^2} + {500^2}\\MA = \sqrt {{x^2} + {{500}^2}} \end{array}\)

Áp dụng định lý Py – ta – go vào tam giác MBB' ta có:

\(\begin{array}{l}M{B^2} = BB{'^2} + MB{'^2} \Rightarrow M{B^2} = {600^2} + {\left( {2200 - x} \right)^2}\\M{B^2} = 360000 + 4840000 - 4400x + {x^2} = 5200000 - 4400x + {x^2}\\MB = \sqrt {5200000 - 4400x + {x^2}} \end{array}\)

Vậy \(MA + MB = \sqrt {{x^2} + {{500}^2}} + \sqrt {5200000 - 4400x + {x^2}} .\)

b. Thay x = 1200vào biểu thức tính MA + MB, ta được:

\(\begin{array}{l}MA + MB = \sqrt {{{1200}^2} + {{500}^2}} + \sqrt {5200000 - 4400.1200 + {{1200}^2}} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {1440000 + 250000} + \sqrt {5200000 - 5280000 + 1440000} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {1690000} + \sqrt {1360000} \\MA + MB \approx 2466\left( {cm} \right) \approx 24\left( m \right).\end{array}\)

Bài 7 trang 66 Toán 9 Tập 1 Cánh diều

Chiều cao ngang vai của một con voi đực ở châu Phi là h (cm) có thể được tính xấp xỉ bằng công thức: \(h = 62,5.\sqrt[3]{t} + 75,8\) với t là tuổi của con voi tính theo năm.

a. Một con voi đực 8 tuổi có chiều cao ngang vai là bao nhiêu centimét?

b. Nếu một con voi đực có chiều cao ngang vai là 205cm thì con voi đó bao nhiêu tuổi (làm tròn kết quả đến hàng đơn vị)?

Hướng dẫn giải:

a. Một con voi đực 8 tuổi thì có chiều cao ngang vai là:

\(h = 62,5.\sqrt[3]{8} + 75,8 = 62,5.2 + 75,8 = 200,8\left( {cm} \right)\)

b. Nếu một con voi đực có chiều cao ngang vai là 205cm thì con voi đó số tuổi là:

\(\begin{array}{l}205 = 62,5\sqrt[3]{t} + 75,8\\\sqrt[3]{t} = 2,0672\\t \approx 9\end{array}\)

Vậy nếu một con voi đực có chiều cao ngang vai là 205cm thì con voi đó 9 tuổi.