Giải Toán 9 trang 107 tập 1 Cánh diều
Giải Toán 9 trang 107 Tập 1
Giải Toán 9 trang 107 Tập 1 Cánh diều hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Cánh diều tập 1 trang 107.
Luyện tập 1 trang 107 Toán 9 Tập 1 Cánh diều
Cho ba điểm A, B, C thẳng hàng, trong đó B nằm giữa A và C. Đường tròn (O) tiếp xúc với đường thẳng AB tại điểm C. Chứng minh AO2 + BC2 = BO2 + AC2.
Hướng dẫn giải
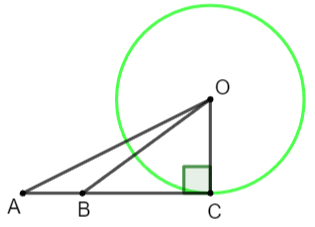
Do (O) tiếp xúc với AB tại C nên OC ⊥ AC
Xét tam giác OAC vuông tại C, ta có:
AO2 = AC2 + CO2 (định lí Pythagore)
Suy ra CO2 = AO2 - AC2 (1)
Xét tam giác OBC vuông tại C, ta có:
BO2 = BC2 + CO2 (định lí Pythagore)
Suy ra CO2 = BO2 - BC2 (2)
Từ (1) và (2) suy ra: AO2 - AC2 = BO2 - BC2
Vậy AO2 + BC2 = BO2 + AC2 (đpcm)
Hoạt động 2 trang 107 Toán 9 Tập 1 Cánh diều
Cho đường thẳng a và đường tròn (O; R) thỏa mãn đường thẳng a đi qua điểm H thuộc đường tròn (O; R) và a vuông góc với OH. Lấy điểm N thuộc đường thẳng a và N khác H (Hình 35).
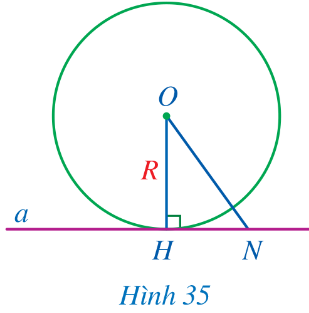
a) So sánh khoảng cách từ điểm O đến đường thẳng a và bán kính R.
b) So sánh ON và R. Điểm N có thuộc đường tròn (O; R) hay không?
c) Đường thẳng a có phải là tiếp tuyến của đường tròn (O; R) hay không?
Hướng dẫn giải
a) Vì OH ⊥ a và H thuộc đường tròn (O; R) nên OH = R
b) Áp dụng quan hệ về đường xiên và đường vuông góc, ta có ON > OH
Mà OH = R nên ON > OH
Do đó điểm N không thuộc đường tròn (O; R).
c) Ta có OH ⊥ a tại H nên a là tiếp tuyến của đường tròn (O; R).
Luyện tập 2 trang 107 Toán 9 Tập 1 Cánh diều
Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài nhau tại điểm I. Gọi d là tiếp tuyến của (O; R) tại điểm I. Chứng minh d là tiếp tuyến của (O'; R').
Hướng dẫn giải
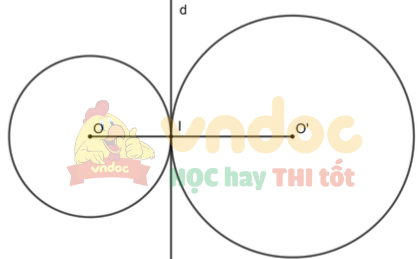
Do (O) và (O') tiếp xúc với nhau tại I nên I thuộc OO'
Mà d là tiếp tuyến của (O) nên d ⊥ OI
Do đó O'I ⊥ d
Suy ra d là tiếp tuyến tại I của (O')
-----------------------------------------------
---> Trang tiếp theo: Giải Toán 9 trang 108 tập 1 Cánh diều
Lời giải Toán 9 trang 107 Tập 1 Cánh diều với các câu hỏi nằm trong Bài 3: Tiếp tuyến của đường tròn, được VnDoc biên soạn và đăng tải!









