Toán 9 Kết nối tri thức Bài tập cuối chương 5

Giải Toán 9 Kết nối tri thức bài 17: Vị trí tương đối của hai đường tròn hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 1 trang 112, 113.

Giải SGK Toán 9 trang 112

Bài 5.32 trang 112 Toán 9 Tập KNTT

Cho đường tròn (O; 4 cm) và hai điểm A, B. Biết rằng OA=\(\sqrt{15}\) cm và OB = 4 cm. Khi đó:

A. Điểm A nằm trong (O), điểm B nằm ngoài (O).

B. Điểm A nằm ngoài (O), điểm B nằm trên (O).

C. Điểm A nằm trên (O), điểm B nằm trong (O).

D. Điểm A nằm trong (O), điểm B nằm trên (O).

Hướng dẫn giải

Đáp án đúng là: D

Vì OA = cm < 4 cm nên điểm A nằm trong (O; 4 cm).

Vì OB = 4 cm nên điểm B nằm trên (O; 4 cm).

Vậy điểm A nằm trong (O), điểm B nằm trên (O).

Bài 5.33 trang 112 Toán 9 Tập KNTT

Cho hình 5.43, trong đó BD là đường kính, \(\hat{AOB}\) =40°;  \(\hat{BOC}\)=100°.

Khi đó:

Hướng dẫn giải:

Vì \(\widehat {DOC}\) và \(\widehat {BOC}\) là hai góc kề bù nên \(\widehat {DOC}+\widehat {BOC}=180^0\).

Suy ra \(\widehat {DOC}=180^0−\widehat {BOC}=18^0−100^0=80^0\).

Do đó sđDC=80° .

Vì \(\widehat {AOD}\) và \(\widehat {AOB}\) là hai góc kề bù nên \(\widehat {AOD}+\widehat {AOB}=180^0\).

Suy ra\(\widehat {AOD}=180°−\widehat {AOB}=180^0−40^0=140^0\).

Do đó sđAD=140° .

Vậy sđDC=80° và sđAD=140° .

Đáp án đúng: D

Bài 5.34 trang 112 Toán 9 Tập KNTT

Cho hai đường tròn (A; R₁), (B; R₂), trong đó R₂ < R₁. Biết rằng hai đường tròn (A) và (B) cắt nhau (H.5.44).

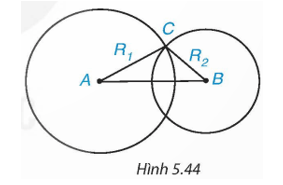
Khi đó:

A. AB < R₁ − R₂.

B. R₁ − R2 < AB < R₁ + R₂.

C. AB > R₁ + R₂.

D. AB = R₁ + R₂.

Hướng dẫn giải

Đáp án đúng là: B

Áp dụng bất đẳng thức trong tam giác ABC, ta có:

AC – BC < AB < AC + BC.

Do đó R₁ − R₂ < AB < R₁ + R₂.

Bài 5.35 trang 112 Toán 9 Tập KNTT

Cho đường tròn (O; R) và hai đường thẳng a₁ và a₂. Gọi d₁, d₂ lần lượt là khoảng cách từ điểm O đến a₁ và a₂. Biết rằng (O) cắt a₁ và tiếp xúc với a₂ (H.5.45).

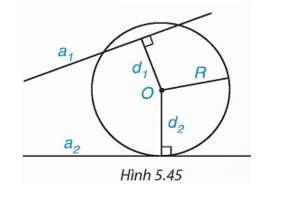
Khi đó:

A. d₁ < R, d₂ = R.

B. d₁ = R, d₂ < R.

C. d₁ > R, d₂ = R.

D. d₁ < R, d₂ < R.

Hướng dẫn giải

Đáp án đúng là: A

• Vì (O) cắt a₁ nên d₁ < R.

• Vì (O) tiếp xúc a₂ nên d₂ = R.

Vậy d₁ < R, d₂ = R.

Bài 5.36 trang 112 Toán 9 Tập KNTT

Cho đường tròn (O) đường kính BC và điểm A (khác B và C).

a) Chứng minh rằng nếu A nằm trên (O) thì ABC là một tam giác vuông; ngược lại, nếu ABC là tam giác vuông tại A thì nằm trên (O).

b) Giả sử A là một trong hai giao điểm của đường tròn (B; BO) với đường tròn (O). Tính các góc của tam giác ABC.

c) Với cùng giả thiết câu b), tính độ dài cung AC và diện tích hình quạt nằm trong (O) giới hạn bởi các bán kính OA và OC, biết rằng BC = 6 cm.

Hướng dẫn giải

Hình vẽ minh họa:

a) Nếu A thuộc (O) thì OA = R

Khi đó tam giác ABC có đường trung tuyến AO bằng nửa cạnh BC nên tg ABC vuông tại A.

Nếu tam giác ABC vuông tại A thì đường trung tuyến AO bằng nửa cạnh huyền BC

Khi đó OA = OB = OC = R. Nghĩa là A thuộc (O).

b) Vì OB = OC = R và A là giao điểm của hai đường tròn.

Suy ra OA = OB = AB = R hay tam giác ABC đều.

Do đó \(\widehat{ABO}=60^{\circ}\) hay \(\widehat{ABC}=60^{\circ}\)

Mà tam giác ABC vuông tại A, suy ra \(\widehat{ACB}=30^{\circ}\)

c) Do \(\widehat{AOB}=60^{\circ}\) (câu b) nên \(\widehat{AOC}=180^{\circ}- 60^{\circ} =120^{\circ}\)

Suy ra sđ \(\overset\frown{AC}\) = 120^o 

Độ dài cung AC là:

\(l=\frac{120}{180}.\pi.3=2\pi\) (cm)

Diện tích hình quạt tròn giới hạn bởi hai bán kính OA và OC ứng với cung 120^o là:

\(S=\frac{120}{360}.\pi.3^2=3\pi\) (cm²)

Giải SGK Toán 9 trang 113

Bài 5.37 trang 113 Toán 9 Tập KNTT

Cho AB là một dây bất kì (không phải là đường kính) của đường tròn (O; 4 cm). Gọi C và D lần lượt là các điểm đối xứng với A và B qua tâm O.

a) Hai điểm C và D có nằm trên đường tròn (O) không? Vì sao?

b) Biết rằng ABCD là một hình vuông. Tính độ dài cung lớn AB và diện tích hình quạt tròn tạo bởi hai bán kính OA và OB.

Hướng dẫn giải

Hình vẽ minh họa:

a) Ta có C, D đối xứng với A, B qua tâm O

Suy ra OA = OB = OC = OD = R

Do đó C và D có nằm trên đường tròn (O)

b) Do ABCD là hình vuông nên AC vuông góc với BD

Số đo cung nhỏ \(\overset\frown{AB}=\widehat{AOB}=90^{\circ}\)

=> Số đo cung lớn AB = 360^o - 90^o = 270^o 

Độ dài cung lớn AB là: 

\(l=\frac{270}{180}.\pi.4=6\pi\) (cm)

Diện tích hình quạt tròn tạo bởi hai bán kính OA và OB là:

\(S=\frac{90}{360}.\pi.4^2=4\pi\) (cm²)

Vậy độ dài cung lớn AB là \(6\pi\), diện tích hình quạt tròn tạo bởi hai bán kính OA và OB là: \(4\pi\).

Bài 5.38 trang 113 Toán 9 Tập KNTT

Cho điểm B nằm giữa hai điểm A và C, sao cho AB = 2 cm và BC = 1 cm. Vẽ các đường tròn (A; 1,5 cm), (B; 3 cm) và (C; 2 cm). Hãy xác định các cặp đường tròn:

a) Cắt nhau;

b) Không giao nhau;

c) Tiếp xúc với nhau.

Hướng dẫn giải

Hình vẽ minh họa: 

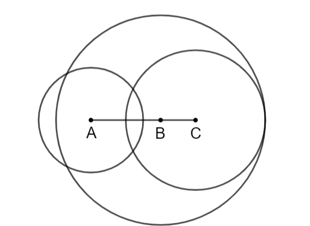
a) Cặp đường thẳng cắt nhau: (A) và (B); (A) và (C).

b) Không có cặp đường tròn nào không giao nhau.

c) Tiếp xúc với nhau: (B) và (C).

Bài 5.39 trang 113 Toán 9 Tập KNTT

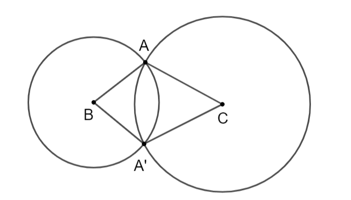
Cho tam giác vuông ABC ( góc A vuông). Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại A và A'. Chứng minh rằng:

a) BA và BA' là hai tiếp tuyến cắt nhau của (C; CA).

b) CA và CA' là hai tiếp tuyến cắt nhau của (B; BA).

Hướng dẫn giải

Hình vẽ minh họa:

a) Xét ΔABC và ΔA'BC có:

BA = BA'

BC chung

CA = CA'

Do đó ΔABC = ΔA'BC (c.c.c).

Suy ra \(\hat{BAC} = \hat{BA'C}\)=90° (hai góc tương ứng)

Khi đó CA′ ⊥ BA′ tại A′ nên BA′ là tiếp tuyến của (C; CA)

Lại có: CA ⊥ BA tại A nên BA là tiếp tuyến của (C; CA)

Vậy CA và CA′ là hai tiếp tuyến cắt nhau của (C; CA).

b) CA′ ⊥ BA′ tại A′ nên CA′ là tiếp tuyến của (B; BA).

CA ⊥ BA tại A nên CA là tiếp tuyến của (B; BA).

Vậy BA và BA′ là hai tiếp tuyến cắt nhau của (B; BA).

Bài 5.40 trang 113 Toán 9 Tập KNTT

Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Một đường thẳng d đi qua A cắt (O) tại E và cắt (O') tại F (E và F) khác A. Biết điểm A nằm trong đoạn EF. Gọi I và K lần lượt là trung điểm của AE và AF (H.5.46).

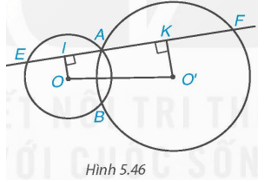
a) Chứng minh rằng tứ giác OO'KI là một hình thang vuông.

b) Chứng minh rằng IK=\(\frac{1}{2}\)EF.

c) Khi d ở vị trí nào (d vẫn qua A) thì OO'KI là một hình chữ nhật?

Hướng dẫn giải

a) Tam giác OAE cân tại O có OI là trung tuyến nên OI cũng là đường cao.

Tam giác O'AF cân tại O có O'K là trung tuyến nên O'K cũng là đường cao.

=> OI // O'K (cùng vuông góc với d).

=> OO'KI là hình thang.

Hình thang OO'KI có \(\widehat {OIA} = {90^0}\) nên OO'KI là một hình thang vuông (đpcm).

b) Vì I là trung điểm của AE nên \(IA = \frac{1}{2}AE\).

Vì K là trung điểm của AF nên \(AK = \frac{1}{2}AF\).

\(\Rightarrow IK = IA + AK = \frac{1}{2}AE + \frac{1}{2}AF = \frac{1}{2}EF\)

Vậy \(IK = \frac{1}{2}EF\).

c) Hình thang OO′KI là hình chữ nhật khi và chỉ khi \(\widehat {OIO\prime } = {90^0}\) hay OI ⊥ OO′.

Mà d ⊥ OI nên d // OO′.

Vậy d vẫn qua A và d // OO′ thì OO'KI là một hình chữ nhật.