Đề thi học kì 2 Toán 9 Chân trời sáng tạo (Cấu trúc mới) Đề 5
Đề kiểm tra cuối kì 2 toán 9 CTST
Đề thi cuối học kì 2 lớp 9 môn Toán sách Chân trời sáng tạo được VnDoc biên soạn bám sát nội dung cấu trúc ma trận đề thi theo Công văn 7991 của Bộ Giáo dục và Đào tạo. Gồm có 3 phần:
- Phần 1: Trắc nghiệm khách quan
- Phần 2: Trắc nghiệm đúng sai
- Phần 3: Tự luận.
Hy vọng thông qua nội dung tài liệu, sẽ giúp bạn học ôn tập, củng cố kiến thức, chuẩn bị tốt cho bài kiểm tra đánh giá học kì 2 môn Toán lớp 9.
|
Trường THCS Đề thi thử số 5 Chân trời sáng tạo |
ĐỀ KIỂM TRA CUỐI HỌC KỲ II MÔN: TOÁN - LỚP 9 NĂM HỌC: 2024 – 2025 Thời gian làm bài: 90 phút |
Họ và tên học sinh: …………………………….. Lớp: …………………………..
PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN (5,0 ĐIỂM)
Thí sinh trả lời từ câu 1 đến câu 20. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.
Câu 1 <NB> Trong các điểm ![]() \(A(1;1),B(
- 2;4),C(10;200),D\left( \sqrt{10};10 \right)\). Có bao nhiêu điểm thuộc đồ thị hàm số
\(A(1;1),B(
- 2;4),C(10;200),D\left( \sqrt{10};10 \right)\). Có bao nhiêu điểm thuộc đồ thị hàm số ![]() \(y =
x^{2}\)?
\(y =
x^{2}\)?
A. ![]() \(1\) B.
\(1\) B. ![]() \(4\) C.
\(4\) C. ![]() \(2\) D.
\(2\) D. ![]() \(3\)
\(3\)
Câu 2: <NB > Điểm ![]() \(A\) thuộc đồ thị hàm số
\(A\) thuộc đồ thị hàm số ![]() \(y = - 2x^{2}\) và có hoành độ bằng
\(y = - 2x^{2}\) và có hoành độ bằng ![]() \(1\) thì có tung độ là
\(1\) thì có tung độ là
A. ![]() \(2\). B.
\(2\). B. ![]() \(- \frac{1}{2}\). C.
\(- \frac{1}{2}\). C. ![]() \(- 2\) . D.
\(- 2\) . D. ![]() \(\frac{1}{2}\).
\(\frac{1}{2}\).
Câu 3: <NB> Cho hàm số ![]() \(y = f(x) =
4x^{2}\) có đồ thị là parabol
\(y = f(x) =
4x^{2}\) có đồ thị là parabol ![]() \((P)\). Xác định tọa độ điểm
\((P)\). Xác định tọa độ điểm ![]() \(A\). Biết điểm
\(A\). Biết điểm ![]() \(A\) nằm trên
\(A\) nằm trên ![]() \((P)\) có hoành độ bằng
\((P)\) có hoành độ bằng ![]() \(- \frac{1}{2}\)?
\(- \frac{1}{2}\)?
A. ![]() \(A\left( - \frac{1}{2}; - 1
\right)\) B.
\(A\left( - \frac{1}{2}; - 1
\right)\) B. ![]() \(A\left( - \frac{1}{2};1
\right)\) C.
\(A\left( - \frac{1}{2};1
\right)\) C. ![]() \(A\left( - \frac{1}{2};\frac{1}{4}
\right)\) D.
\(A\left( - \frac{1}{2};\frac{1}{4}
\right)\) D. ![]() \(A\left( - \frac{1}{2}; - 2
\right)\)
\(A\left( - \frac{1}{2}; - 2
\right)\)
Câu 4: Tổng tất cả các nghiệm của phương trình ![]() \(x^{2} - x - 20 = 0\) bằng:
\(x^{2} - x - 20 = 0\) bằng:
A. ![]() \(1\) B.
\(1\) B. ![]() \(9\) C.
\(9\) C. ![]() \(- 3\) D.
\(- 3\) D. ![]() \(2\)
\(2\)
Câu 5: <VD> Cho phương trình ![]() \(x^{2}
- mx + m - 2 = 0\\)hai nghiệm phân biệt
\(x^{2}
- mx + m - 2 = 0\\)hai nghiệm phân biệt ![]() \(x_{1},x_{2}\) để
\(x_{1},x_{2}\) để ![]() \(x_{1}^{2} + x_{2}^{2} = 7\). Tổng các giá trị của
\(x_{1}^{2} + x_{2}^{2} = 7\). Tổng các giá trị của ![]() \(m\) bằng:
\(m\) bằng:
A. ![]() \(4\). B.
\(4\). B. ![]() \(- 4\). C.
\(- 4\). C. ![]() \(- 2\). D.
\(- 2\). D. ![]() \(2\).
\(2\).
Câu 6 <TH> Sau khi điều tra 48 hộ gia đình ở vùng dân cư về số nhân khẩu của mỗi hộ gia đình, người ta được dãy số liệu sau:
|
5 |
4 |
6 |
7 |
5 |
5 |
4 |
3 |
|
6 |
5 |
6 |
7 |
5 |
8 |
6 |
5 |
|
4 |
5 |
5 |
6 |
6 |
4 |
5 |
7 |
|
6 |
4 |
5 |
6 |
5 |
7 |
4 |
5 |
|
6 |
5 |
4 |
4 |
6 |
7 |
5 |
6 |
|
5 |
4 |
5 |
7 |
6 |
4 |
5 |
6 |
Chọn biểu đồ tần số tương đối ứng với dãy số liệu đã cho?
A.![]()
B.![]()
C. ![]()
D. ![]()
Câu 7 <NB> Trong bài thơ “Quê hương” của tác giả Đỗ Trung Quân có hai câu thơ:
“Quê hương nếu ai không nhớ
Sẽ không lớn nổi thành người”.
Mẫu dữ liệu thống kê các chữ cái H; N; G; L lần lượt xuất hiện trong hai câu thơ trên là: H; N; G; N; H; N; G; N; H; H; N; G; L; N; N; H; N; H; N; G.
Tần số tương đối của giá trị nào là lớn nhất?
A. H B. G C. L D. N
Câu 8: <NB> Kết quả điều tra cân nặng của một số học sinh lớp 9 được ghi lại trong bảng sau:
|
Cân nặng (Kg) |
47 |
48 |
49 |
50 |
52 |
|
Số học sinh |
2 |
8 |
3 |
5 |
2 |
Hãy cho biết số học sinh có cân nặng ít nhất là 49 kg là bao nhiêu em?
A. 8 B. 7 C. 10 D. 13
Câu 9: <TH> Khảo sát một số bạn học sinh trong lớp 9A về thể loại phim yêu nhất. Mỗi bạn chỉ chọn đúng một thể loại phim. Kết quả được cho ở bảng sau:
|
Thể loại |
Hài |
Kinh dị |
Khoa học viễn tưởng |
|
Tần số |
20 |
8 |
12 |
Chọn biểu đồ tần số tương đối thích hợp?
A. 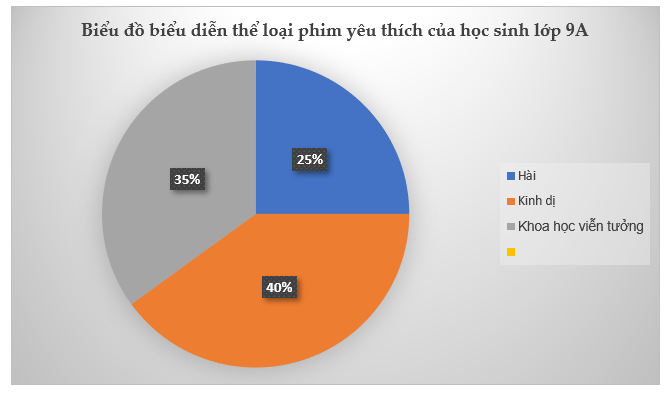 B.
B. 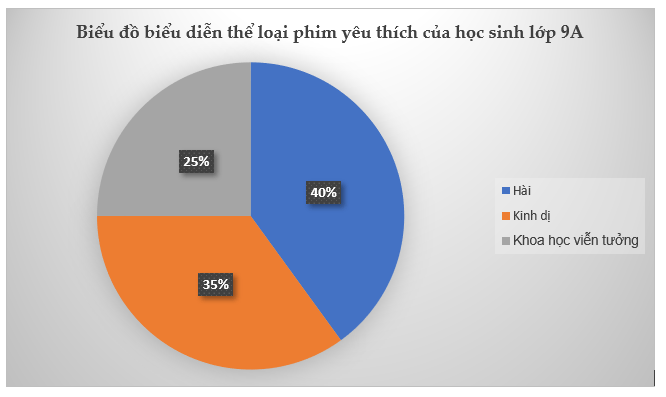
C. 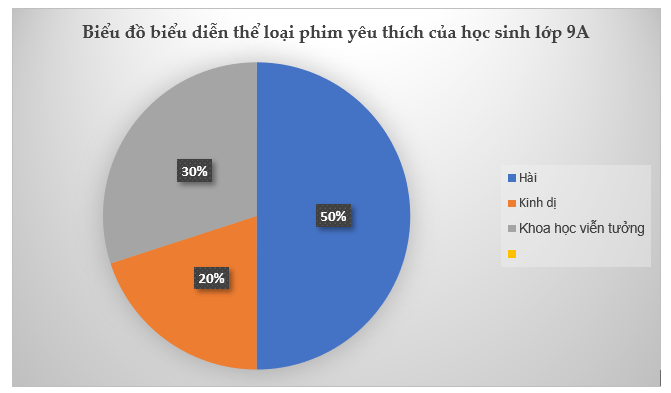 D.
D. 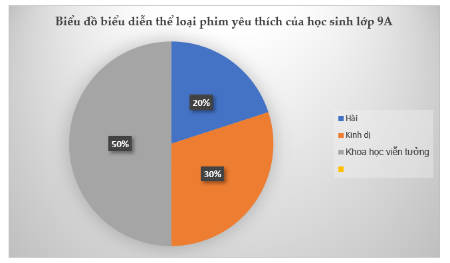
Câu 10: <TH> Chiều cao của một nhóm học sinh 30 em ( đơn vị mét) lớp 9A2 được ghi lại ở bảng sau:
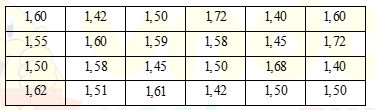
Bảng tần số tương đối ghép nhóm với các nhóm ![]() \(\lbrack 1,40;1,55)\);
\(\lbrack 1,40;1,55)\); ![]() \(\lbrack 1,55;1,65)\);
\(\lbrack 1,55;1,65)\); ![]() \(\lbrack 1,65;1,72\rbrack\) lập được từ bảng số liệu trên là
\(\lbrack 1,65;1,72\rbrack\) lập được từ bảng số liệu trên là
A. 
B. 
C. 
D. 
Câu 11: <NB> Gieo hai đồng tiền một lần. Kí hiệu ![]() \(S;\ N\) để chỉ đồng tiền lật sấp, lật ngửa. Mô tả không gian mẫu của phép thử trên
\(S;\ N\) để chỉ đồng tiền lật sấp, lật ngửa. Mô tả không gian mẫu của phép thử trên
A. ![]() \(\Omega = \left\{ SS;\ NN;\ SN;\ NS
\right\}\) B.
\(\Omega = \left\{ SS;\ NN;\ SN;\ NS
\right\}\) B. ![]() \(\Omega = \left\{ S;\ N;\ N;\ S
\right\}\)
\(\Omega = \left\{ S;\ N;\ N;\ S
\right\}\)
C. ![]() \(\Omega = \left\{ SS;\ NN
\right\}\) D.
\(\Omega = \left\{ SS;\ NN
\right\}\) D. ![]() \(\Omega = \left\{ SN;\ NS
\right\}\)
\(\Omega = \left\{ SN;\ NS
\right\}\)
Câu 12: <NB> Một lớp học có 60 học sinh, trong đó 15 học sinh tham gia câu lạc bộ toán học. Xác suất chọn 1 học sinh CLB Toán học của lớp để tham gia biểu diễn là:
A. ![]() \(0,15\). B.
\(0,15\). B. ![]() \(0,25\). C.
\(0,25\). C. ![]() \(0,4\). D.
\(0,4\). D. ![]() \(\frac{1}{2}\).
\(\frac{1}{2}\).
Câu 13: <TH> Cho tập hợp ![]() \(A =
\left\{ 1;\ 0;\ 5;\ 6 \right\}\). Bạn Mai dùng
\(A =
\left\{ 1;\ 0;\ 5;\ 6 \right\}\). Bạn Mai dùng ![]() \(2\) chữ số khác nhau từ
\(2\) chữ số khác nhau từ ![]() \(A\) để tạo thành số có
\(A\) để tạo thành số có ![]() \(2\) chữ số. Xác suất của biến cố: “Số tạo thành chia hết cho
\(2\) chữ số. Xác suất của biến cố: “Số tạo thành chia hết cho ![]() \(5\)” là.
\(5\)” là.
A. ![]() \(\frac{1}{2}\). B.
\(\frac{1}{2}\). B. ![]() \(\frac{5}{9}\). C.
\(\frac{5}{9}\). C. ![]() \(\frac{4}{9}\) . D.
\(\frac{4}{9}\) . D. ![]() \(\frac{1}{3}\).
\(\frac{1}{3}\).
Câu 14: <VD> Một tổ học sinh có ![]() \(3\) nam và
\(3\) nam và ![]() \(7\) nữ. Chọn ngẫu nhiên đồng thời
\(7\) nữ. Chọn ngẫu nhiên đồng thời ![]() \(2\) người. Tính xác suất sao cho
\(2\) người. Tính xác suất sao cho ![]() \(2\) người được chọn đều là nữ
\(2\) người được chọn đều là nữ
A. ![]() \(\frac{7}{15}\). B.
\(\frac{7}{15}\). B. ![]() \(\frac{1}{15}\). C.
\(\frac{1}{15}\). C. ![]() \(\frac{8}{15}\). D.
\(\frac{8}{15}\). D. ![]() \(\frac{1}{5}\).
\(\frac{1}{5}\).
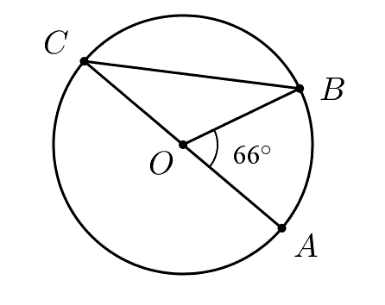
Câu 15: <TH> Cho ![]() \(\widehat{AOB} =
66{^\circ}\) như hình vẽ. Số đo của
\(\widehat{AOB} =
66{^\circ}\) như hình vẽ. Số đo của ![]() \(\widehat{OCB}\) là
\(\widehat{OCB}\) là
A. ![]() \(132{^\circ}\). B.
\(132{^\circ}\). B. ![]() \(33{^\circ}\). C.
\(33{^\circ}\). C. ![]() \(24{^\circ}\). D.
\(24{^\circ}\). D. ![]() \(114{^\circ}\).
\(114{^\circ}\).
Câu 16: <NB> Tâm đường tròn ngoại tiếp tam giác là:
A. Giao của ba đường phân giác.
B. Giao của ba đường trung trực.
C. Giao của ba đường cao.
D. Giao của ba đường trung tuyến.
Câu 17: <NB> Số đường tròn nội tiếp của một tam giác đều là
A. ![]() \(1\). B.
\(1\). B. ![]() \(2\). C.
\(2\). C. ![]() \(3\). D.
\(3\). D. ![]() \(0\).
\(0\).
Câu 18: <NB> Các hình nào sau đây nội tiếp đường tròn?
A. Hình thoi, hình chữ nhật. B. Hình vuông, hình bình hành.
C. Hình thoi, hình vuông. D. Hình chữ nhật, hình vuông.
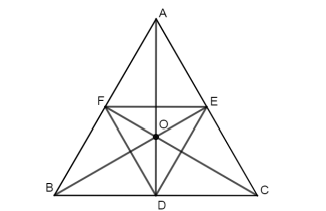
Câu 19: <NB> Cho tam giác ABC đều có O là trọng tâm, gọi ![]() \(D,E,F\) lần lượt là trung điểm các cạnh
\(D,E,F\) lần lượt là trung điểm các cạnh ![]() \(BC,CA,AB\). Phép quay thuận chiều tâm O góc quay 120° biến điểm F thành điểm nào dưới đây?
\(BC,CA,AB\). Phép quay thuận chiều tâm O góc quay 120° biến điểm F thành điểm nào dưới đây?
A. Điểm E. B. Điểm A. C. Điểm B. D. Điểm D
Câu 20: <TH> Cho hình cầu có diện tích bề mặt là ![]() \(324\pi\ \ \left( cm^{2} \right)\). Thể tích hình cầu đó là
\(324\pi\ \ \left( cm^{2} \right)\). Thể tích hình cầu đó là
A. ![]() \(792\pi\ \ \left( cm^{3}
\right)\). B.
\(792\pi\ \ \left( cm^{3}
\right)\). B. ![]() \(108\pi\ \ \left( cm^{3}
\right)\). C.
\(108\pi\ \ \left( cm^{3}
\right)\). C. ![]() \(972\pi\ \ \left( cm^{3}
\right)\). D.
\(972\pi\ \ \left( cm^{3}
\right)\). D. ![]() \(972\ \ \left( cm^{3}
\right)\).
\(972\ \ \left( cm^{3}
\right)\).
PHẦN II. PHẦN TRẮC NGHIỆM ĐÚNG SAI (2,0 ĐIỂM)
Thí sinh trả lời câu hỏi sau, trong mỗi ý a), b), c), d) thí sinh chọn đúng hoặc sai
Câu 21: Cho phương trình ![]() \(x^{2} - 4x -
m^{2} - 1 = 0\)
\(x^{2} - 4x -
m^{2} - 1 = 0\)
a. <NB> Hệ số a là -4.
b. <NB> Biệt thức  \(\Delta^{'} =
m^{2} + 5\).
\(\Delta^{'} =
m^{2} + 5\).
c. <TH> Tổng hai nghiệm bằng 4.
d) <VD> Khi ![]() \(m = \pm 2\) thì phương trình có hai nghiệm phân biệt
\(m = \pm 2\) thì phương trình có hai nghiệm phân biệt ![]() \(x_{1},\
x_{2}\) thỏa mãn
\(x_{1},\
x_{2}\) thỏa mãn![]() \(x_{2} = -
5x_{1}\) .
\(x_{2} = -
5x_{1}\) .
Câu 22: Gieo một con xúc xắc cân đối đồng chất một lần.
a) <NB> Nếu gieo con xúc xắc 36 lần và có 6 lần xuất hiện mặt 1 chấm thì xác suất thực nghiệm của biến cố “Xuất hiện mặt một chấm” ước lượng khoảng ![]() \(\frac{1}{6}.\)
\(\frac{1}{6}.\)
b) <NB> Xác suất xuất hiện măt có số chấm là số lẻ là ![]() \(\frac{1}{2}.\)
\(\frac{1}{2}.\)
c) <TH> Xác suất xuất hiện mặt có số chấm là số nguyên tố là ![]() \(\frac{1}{3}\).
\(\frac{1}{3}\).
d) <VD> Xác suất để phương trình ![]() \(x^{2} - ax + 3 = 0\) có nghiệm là 3 (với a là số chấm xuất hiện khi tung xúc xắc) là
\(x^{2} - ax + 3 = 0\) có nghiệm là 3 (với a là số chấm xuất hiện khi tung xúc xắc) là ![]() \(\frac{1}{6}\)
\(\frac{1}{6}\)
PHẦN III. TỰ LUẬN (3,0 ĐIỂM)
Thí sinh trình bày lời giải chi tiết.
Câu 23: Cho phương trình ![]() \(x^{2} - 2(m +
1)x + 4m = 0\).
\(x^{2} - 2(m +
1)x + 4m = 0\).
a) Giải phương trình với m =1
b) Tìm ![]() \(m\) để phương trình có hai nghiệm phân biệt
\(m\) để phương trình có hai nghiệm phân biệt ![]() \(x_{1},x_{2}\)thỏa mãn
\(x_{1},x_{2}\)thỏa mãn ![]() \(x_{1} = - 3x_{2}\)
\(x_{1} = - 3x_{2}\)
Câu 24: Cho ![]() \(\Delta ABC\)vuông tại
\(\Delta ABC\)vuông tại ![]() \(C\) có
\(C\) có ![]() \((AC < BC)\), đường cao
\((AC < BC)\), đường cao ![]() \(CK\) và đường phân giác
\(CK\) và đường phân giác ![]() \(BD(K \in AB;\ D \in AC)\)Qua
\(BD(K \in AB;\ D \in AC)\)Qua ![]() \(D\)kẻ đường thẳng vuông góc với AC cắt
\(D\)kẻ đường thẳng vuông góc với AC cắt ![]() \(CK,\ AB\) lần lượt tại
\(CK,\ AB\) lần lượt tại ![]() \(H\) và
\(H\) và ![]() \(I\).
\(I\).
a.Chứng minh tứ giác ![]() \(CDKI\) nội tiếp một đường tròn.
\(CDKI\) nội tiếp một đường tròn.
b.Chứng minh ![]() \(AK.CI = AH.CK\).
\(AK.CI = AH.CK\).
c.Gọi ![]() \(F\) là trung điểm của
\(F\) là trung điểm của ![]() \(AD\) đường tròn tâm
\(AD\) đường tròn tâm ![]() \(I\) bán kính
\(I\) bán kính ![]() \(ID\) cắt
\(ID\) cắt ![]() \(BC\) tại
\(BC\) tại ![]() \(M\)(
\(M\)(![]() \(M\) khác
\(M\) khác ![]() \(B\)) và cắt
\(B\)) và cắt ![]() \(AM\) tại
\(AM\) tại ![]() \(N\)(
\(N\)(![]() \(N\) khác
\(N\) khác ![]() \(M\)). Chứng minh ba điểm
\(M\)). Chứng minh ba điểm ![]() \(B,\ N,\ F\) thẳng hàng.
\(B,\ N,\ F\) thẳng hàng.
Câu 25: Một khối gỗ hình trụ có chiều cao gấp 3 lần đường kính đáy, Biết diện tích toàn phần của khối gỗ là ![]() \(7\pi\left( m^{2} \right)\). Tính thế tích của khối gỗ theo đơn vị
\(7\pi\left( m^{2} \right)\). Tính thế tích của khối gỗ theo đơn vị ![]() \(m^{3}\). (Lấy
\(m^{3}\). (Lấy ![]() \(\pi \approx 3,14\) và làm tròn kết quả đến hai chữ số thập phân).
\(\pi \approx 3,14\) và làm tròn kết quả đến hai chữ số thập phân).
- Hết -
------------------------------------------
Mời bạn đọc tải tài liệu tham khảo đáp án chi tiết!










