Đề thi học kì 2 Toán 9 Kết nối tri thức CV 7991 Đề 3

Đề kiểm tra cuối kì 2 toán 9

Đề thi cuối học kì 2 lớp 9 môn Toán sách Kết nối tri thức được VnDoc biên soạn bám sát nội dung cấu trúc ma trận đề thi theo Công văn 7991 của Bộ Giáo dục và Đào tạo. Gồm có 3 phần:

• Phần 1: Trắc nghiệm khách quan
• Phần 2: Trắc nghiệm đúng sai
• Phần 3: Tự luận.

Hy vọng thông qua nội dung tài liệu, sẽ giúp bạn học ôn tập, củng cố kiến thức, chuẩn bị tốt cho bài kiểm tra đánh giá học kì 2 môn Toán lớp 9.

Họ và tên học sinh: …………………………….. Lớp: …………………………..

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN (5,0 ĐIỂM)

Thí sinh trả lời từ câu 1 đến câu 20. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1. Cho hàm số \(y = 2x^{2}.\) Khẳng định nào sau đây là đúng?

A. Đồ thị hàm số nhận trục hoành làm trục đối xứng.

B. Đồ thị hàm số nhận trục tung làm trục đối xứng.

C. Đồ thị hàm số nằm phía dưới trục hoành.

D. Đồ thị hàm số nằm bên phải trục tung.

Câu 2. Điểm nào sau đây thuộc đồ thị hàm số \(y = - \frac{1}{2}x^{2}\)?

A. \(\left( 1; - \frac{1}{2} \right)\).

B. \((1; - 2)\).

C. \(( - 2;1)\).

D. \(\left( - 1;\frac{1}{2} \right)\).

Câu 3. Giá trị của hàm số \(y = - 3x^{2}\) tại \(x = - 2\) là:

A. \(12.\)

B. \(- 6\).

C. \(- 12.\)

D. \(6\).

Câu 4. Trong các phương trình sau, phương trình nào là phương trình bậc hai một ẩn?

A. \(0x^{2}–3x + 2 = 0.\)

B. \(x + 3 = 0\).

C. \(x^{2} - 3xy + 4 = 0\).

D. \(3x^{2} - 5x + 2 = 0\).

Câu 5. Nếu \(x_{1},x_{2}\) là hai nghiệm của phương trình \(x^{2}–3x + 2 = 0\) thì \(x_{1} + x_{2}\) bằng

A. \(3.\)

B. \(- 3\).

C. \(- 2\).

D. \(2\).

Câu 6. Điều tra về sự tiêu thụ điện năng (tính theo kwh) của một số gia đình ở một

tổ dân số, ta có kết quả sau:

Có bao nhiêu hộ gia đình tham gia điều tra?

A. \(22.\)

B. \(20.\)

C. \(28.\)

D. \(30.\)

Câu 7. Thời gian giải bài toán (tính theo phút) của học sinh lớp 9 được ghi lại trong

bảng sau:

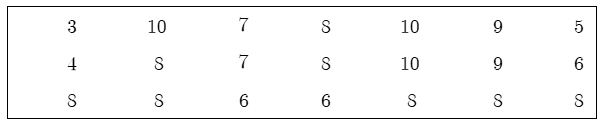
Số các giá trị khác nhau của dấu hiệu là:

A. \(5.\)

B. \(6.\)

C. \(7.\)

D. \(8.\)

Câu 8. Điều tra về sự tiêu thụ điện năng (tính theo kwh) của một số gia đình ở một

tổ dân phố, ta có kết quả sau:

Có bao nhiêu hộ gia đình tiêu thụ với mức điện năng nhỏ hơn 100 kwh?

A. \(20.\)

B. \(10.\)

C. \(12.\)

D. \(15.\)

Câu 9. Tần số tương đối của “Tỉ lệ học sinh bình chọn rơi vào khối \(6\)” trong bảng

sau là bao nhiêu?

A. \(32\%\).

B. \(23,5\%\).

C. \(30\%\).

D. \(14,5\%\).

Câu 10. Có mấy loại dữ liệu khác nhau trong bảng tần số tương đối sau:

A.\(1\).

B. \(2\).

C. \(3\).

D. \(4.\)

Câu 11. Gieo hai đồng tiền một lần. Kí hiệu \(S;\ N\) để chỉ đồng tiền lật sấp, lật ngửa.

Mô tả không gian mẫu của phép thử trên:

A. \(\Omega = \left\{ SS;\ NN;\ SN;\ NS \right\}\).	B. \(\Omega = \left\{ S;\ N;\ N;\ S \right\}\).
C. \(\Omega = \left\{ SS;\ NN \right\}\).	D. \(\Omega = \left\{ SN;\ NS \right\}\).

Câu 12. Một lớp học có 60 học sinh, trong đó 15 học sinh tham gia câu lạc bộ toán

học. Xác suất chọn 1 học sinh CLB Toán học của lớp để tham gia biểu diễn là:

A. \(0,15\).

B. \(0,25\).

C. \(0,4\).

D. \(\frac{1}{2}\).

Câu 13. Gieo đồng thời hai con xúc xắc cân đối, đồng chất. Xác suất của biến cố

“Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 9” là:

A. \(\frac{1}{4}.\)

B. \(0.\)

C.\(\frac{1}{2}.\)

D. \(\frac{1}{3}.\)

Câu 14. Cho tập hợp \(A = \left\{ 1;\ 0;\ 5;\ 6 \right\}\). Bạn Linh dùng \(2\) chữ số khác nhau từ \(A\) để tạo

thành số có \(2\) chữ số. Xác suất của biến cố: “Số tạo thành chia hết cho \(5\)” là.

A. \(\frac{1}{2}\).

B. \(\frac{5}{9}\).

C. \(\frac{4}{9}\) .

D. \(\frac{1}{3}\).

Câu 15. Cho \(\widehat{AOB} = 66{^\circ}\) như hình vẽ. Số đo của \(\widehat{OCB}\) là:

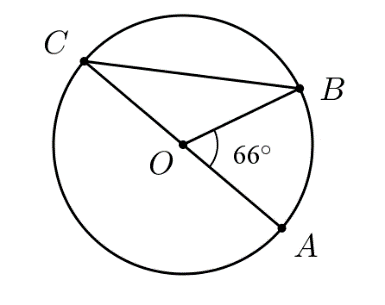
A. \(132{^\circ}\).

B. \(33{^\circ}\).

C. \(24{^\circ}\).

D. \(114{^\circ}\).

Câu 16. Tâm đường tròn ngoại tiếp tam giác là giao điểm của các đường

Câu 17. Cho tam giác \(ABC\) vuông tại A, có \(AB = 3\) cm, \(AC = 4\) cm. Độ dài của bán kính đường tròn ngoại tiếp tam giác \(ABC\) là

A. \(5\ \ cm\).

B. \(2cm\).

C. \(3,5\ \ cm\).

D. \(2,5\ \ cm\).

Câu 18. Cho tứ giác\(ABCD\) nội tiếp được đường tròn, Biết \(\widehat{C} = 60^{0},\widehat{D} = 80^{0}\). Khi đó:

A. \(\widehat{A} = 60^{0};\widehat{B} = 80^{0}\).	B. \(\widehat{A} = 120^0;\widehat{B} =100^0\).
C. \(\widehat{A} = 120^{0};\widehat{B} = 130^{0}\).	D. \(\widehat{A} = 90^{0};\widehat{B} = 100^{0}\)

Câu 19. Khi quay một hình chữ nhật quanh một cạnh của nó ta thu được

Câu 20. Cho mặt cầu có thể tích \(V = 288\pi\)(cm³). Tính đường kính mặt cầu:

A. \(6cm\).

B. 12cm.

C. \(8cm.\)

D. \(16cm.\)

PHẦN II. PHẦN TRẮC NGHIỆM ĐÚNG SAI (2,0 ĐIỂM)

Thí sinh trả lời câu 21 và câu 22. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 21. Cho phương trình \(x^{2} - 5x + m + 4 = 0\)

a) Hệ số b của phương trình là \(5.\)

b) Biệt thức \(\Delta = - 4m + 9.\)

c) Phương trình đã cho có hai nghiệm phân biệt khi \(m < \frac{9}{4}.\)

d) Khi \(m = 29\) thì phương trình có hai nghiệm phân biệt \(x_{1},\ x_{2}\) thỏa mãn hệ thức\(\frac{x_{1}}{x_{2}} + \frac{x_{2}}{x_{1}} = - 3.\)

Câu 22. Một cuộc thi bắn cung có 20 người tham gia. Trong lần bắn đầu tiên có 18 người bắn trúng mục tiêu. Trong lần bắn thứ hai có 15 người bắn trúng mục tiêu. Trong lần bắn thứ ba chỉ có 17 người bắn trúng mục tiêu.

a) Số người bắn trúng mục tiêu lần đầu là 18.

b) Tỉ lệ người bắn trượt mục tiêu lần thứ hai là 25%.

c) Tỉ lệ người bắn trượt mục tiêu trong lần bắn thứ nhất lớn hơn trong lần bắn thứ hai là 15%.

d) Tần suất trung bình người bắn trượt trong cả ba lần bắn lớn hơn 10%.

PHẦN III. TỰ LUẬN (3,0 ĐIỂM)

Câu 23. Cho phương trình \(x^{2} - 2x - m = 0\).

a) Giải phương trình với \(m = 3.\)

b) Tìm \(m\) để phương trình có hai nghiệm phân biệt \(x_{1},x_{2}\) thỏa mãn

\(x_{1}^{2} + x_{2}^{2} + x_{1} + x_{2} = 2024.\)

Câu 24. Từ điểm \(A\) bên ngoài đường tròn \((O)\) vẽ hai tiếp tuyến \(AB,\ AC\ \ (B,\ C\) là các tiếp điểm). Qua \(A\) vẽ cát tuyến \(AMN\) với đường tròn \((O)\) không đi qua tâm \(O\ \ (M\) nằm giữa \(A\) và \(N).\)

a) Chứng minh rằng bốn điểm \(A,\ B,\ C,\ O\) cùng nằm trên một đường tròn.

b) Chứng minh rằng tam giác \(AMB\) đồng dạng với tam giác \(ABN.\)

c) Chứng minh rằng \(\frac{AM}{AB} = \frac{AC}{AN}\).

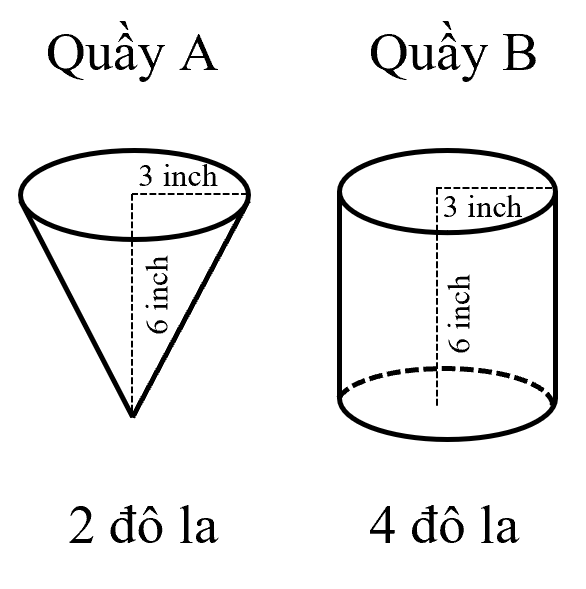
Câu 25. Ở hai quầy hàng A và B trong một hội hoa xuân người ta bán cùng 1 loại hạt bắp rang bơ lần lượt được đựng trong hai loại hộp hình nón và hình trụ với thông tin giá cả và định lượng như trong hình dưới đây. Vỏ hộp đều được làm từ giấy phần này nhận được sự tài trợ của công ty giấy nên cả hai quầy không tốn chi phí làm vỏ hộp. Hỏi bạn H nên mua bắp rang bơ ở quầy A hay quầy B để có lợi hơn ? Tại sao?

……………………….HẾT…………………….

Mời bạn đọc tải tài liệu tham khảo đáp án chi tiết của đề thi!