Đề thi học kì 2 Toán 9 Chân trời sáng tạo (Cấu trúc mới) Đề 3

Đề kiểm tra cuối kì 2 toán 9 CTST

Đề thi cuối học kì 2 lớp 9 môn Toán sách Chân trời sáng tạo được VnDoc biên soạn bám sát nội dung cấu trúc ma trận đề thi theo Công văn 7991 của Bộ Giáo dục và Đào tạo. Gồm có 3 phần:

• Phần 1: Trắc nghiệm khách quan
• Phần 2: Trắc nghiệm đúng sai
• Phần 3: Tự luận.

Hy vọng thông qua nội dung tài liệu, sẽ giúp bạn học ôn tập, củng cố kiến thức, chuẩn bị tốt cho bài kiểm tra đánh giá học kì 2 môn Toán lớp 9.

Trường THCS Đề thi thử số 3 Chân trời sáng tạo

ĐỀ KIỂM TRA CUỐI HỌC KỲ II MÔN: TOÁN - LỚP 9 NĂM HỌC: 2024 – 2025 Thời gian làm bài: 90 phút

Họ và tên học sinh: …………………………….. Lớp: …………………………..

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN (5,0 ĐIỂM)

Thí sinh trả lời từ câu 1 đến câu 20. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Cho hàm số $y=x^2$. Kết luận nào sau đây là đúng?

A. Đồ thị hàm số nhận trục hoành làm trục đối xứng

B. Đồ thị hàm số nằm phía trên trục hoành và O là điểm cao nhất

C. Đồ thị hàm số nằm phía trên trục hoành và O là điểm thấp nhất.

D. Đồ thị hàm số nằm phía dưới trục hoành và O là điểm thấp nhất

Câu 2. Giá trị của hàm số $y=f(x)=\frac{1}{2}{x}^2$ tại $x_0=-2$ là:

A. $2.$                      B. $-2.$              C. $1.$              D. $-1.$

Câu 3. Cho phương trình $a{x}^2+bx+c=0(a\ne 0)$ có biệt thức $\mathrm{\Delta }=b^2-4ac=0$, khi đó phương trình đã cho có hai nghiệm là:

A. $x_1=x_2=\frac{b}{2a}$                                                   B. $x_1=-\frac{b}{2a};x_2=\frac{b}{2a}$

C. $x_1=\frac{-b+\sqrt{\mathrm{\Delta }}}{2a};x_2=\frac{-b-\sqrt{\mathrm{\Delta }}}{2a}$                      D. $x_1=x_2=\frac{-b}{2a}$

Câu 4. Chỉ ra phương trình nào dưới đây là phương trình bậc hai một ẩn?

A. $2x^2-3\sqrt{x}+1=0$                    B. $5x^2-1010=0$

C. $7x+\frac{2}{x}-3=0$                         D. $4x-1=0$

Câu 5. Một nhóm học sinh mua tổng cộng $15$ cốc trà sữa và hồng trà. Giá của cốc trà sữa, hồng trà lần lượt là $25000$ đồng và $22000$ đồng. Tổng số tiền nhóm học sinh đó phải trả là $363000$ đồng. Gọi $x;y$ lần lượt là số cốc trà sữa và hồng trà nhóm học sinh đó đã mua. Khi đó điều kiện của hai ẩn $x;y$ là

A. $x;y\in N;x\le 15.$                                 B. $x;y\in N;x\le 15,y\le 15.$

C. $x;y\in N;x\le y\le 15.$                          D. $x;y\in N;x>y\ge 15.$

Câu 6: Cho phương trình$a{x}^2+bx+c=0(a\ne 0)$ nếu $a+b+c=0$thì nghiệm của phương trình là

A. $x_1=1;x_2=\frac{-c}{a}$                               B. $x_1=1;x_2=\frac{c}{a}$

C. $x_1=-1;x_2=\frac{c}{a}$                               D. $x_1=-1;x_2=\frac{-c}{a}$

Câu 7: Gọi $x_1;x_2$ là nghiệm của phương trình $x^2-5x+2=0$. Không giải phương trình, tính giá trị biểu thức A = $x_1^2+x_2^2$

A. $20.$                         B. $21.$                     C. $22.$                        D. $23.$

Câu 8: Bảng thống kê cho biết tần số của các giá trị trong mẫu dữ liệu được gọi là

A. Tần số.                                    B. Mẫu dữ liệu.

C. Bảng tần số.                            D. Biểu đồ tần số.

Câu 9: Cho bảng thống kê số lượt mượn các loại sách tại thư viện của trường THCS A:

Loại sách	Sách giáo khoa	Sách tham khảo	Truyện ngắn	Truyện tranh
Số lượt mượn	30	65	55	100

Biểu đồ nào dưới đây biểu diễn cho bảng thống kê đã cho?

A.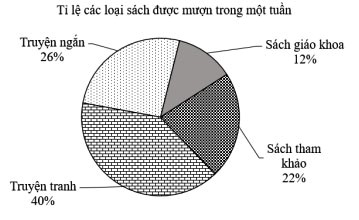                B.

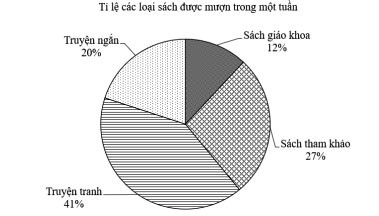C.            D.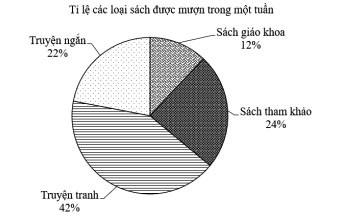

Câu 10. Gieo một con xúc xắc cân đối và đồng chất. Không gian mẫu của phép thử có số phần tử là

A. 6.                        B. 4.                   C. 5.                     D. 3.

Câu 11. Trong một đường tròn, cho góc $\widehat{AMB}$ là góc nội tiếp chắn nửa đường tròn. Khẳng định nào sau đây là đúng?

A. $\widehat{AMB}$ là góc nhọn.                    B. $\widehat{AMB}={90}^0$ .

C. $\widehat{AMB}$ là góc tù.                          D. $\widehat{AMB}={180}^0$.

Câu 12. Tâm đường tròn nội tiếp của một tam giác là giao của các đường

A. Phân giác.              B. Trung trực.            C. Đường cao.         D. Trung tuyến.

Câu 13. Đường tròn ngoại tiếp tam giác đều cạnh a có bán kính bằng:

A. $\frac{a\sqrt{3}}{6}$               B. $\frac{a\sqrt{3}}{3}$                  C. $\frac{a}{6}$                           D. $\frac{a}{3}$

Câu 14. Biết độ dài các cạnh của mỗi tam giác trong các hình sau bằng nhau, có tất cả bao nhiêu tam giác đều?

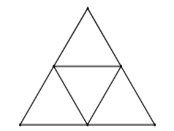
A. $5$                            B. $4$                                C. $3$                       D. $6$

Câu 15.  Cho tam giác $ABC$ có ba góc nhọn, đường cao $AH$ và nội tiếp đường tròn tâm (O), đường kính $AM$. Số đo góc $\widehat{ABM}$ là

A. ${60}^o$                      B. ${45}^o$                        C. ${90}^o$                      D. ${100}^o$

Câu 16. Cho $\mathrm{\Delta }ABC$ vuông tại A. Biết$AB=3cm$; $AC=4cm$. Bán kính đường tròn ngoại tiếp $\mathrm{\Delta }ABC$ là

A. $10cm.$                    B. $5cm.$                         C. $2,5cm.$                     D. $10,5cm.$

Câu 17. Hình chữ nhật có chiều dài 8cm, chiều rộng 6cm. Quay hình chữ nhật đó một vòng quanh chiều dài của nó ta được một hình trụ có chiều cao h và bán kình đáy r là

A. $r=8cm;h=6cm.$                 B. $r=4cm;h=3cm.$

C. $r=3cm;h=4cm.$                  D. $r=6cm;h=8cm.$

Câu 18. Cho một hình cầu và một hình lập phương ngoại tiếp nó. Tính tỉ số giữa diện tích mặt cầu và diện tích toàn phần của hình lập phương.

A. $\frac{6}{\pi }$.                  B. $\frac{1}{6}$.                       C. $\frac{\pi }{6}$.                       D. $\frac{1}{3}$.

Câu 19. Cho hình chữ nhật có chiều dài 3 cm, chiều rộng 2 cm. Quay hình chữ nhật đó một vòng quanh chiều dài của nó ta được một hình trụ có diện tích xung quanh bằng

A. $6\pi \left(c{m}^2\right)$               B. $8\pi \left(c{m}^2\right)$            C. $12\pi \left(c{m}^2\right)$                    D. $18\pi \left(c{m}^2\right)$

Câu 20. Thể tích của một hình cầu là $\frac{4312}{3}$ cm${}^3$. Thì bán kính của hình cầu là bao nhiêu? (Lấy $\pi =\frac{22}{7}$).

A. $7$ cm.                  B. $8$ cm.                   C. $9$ cm.                          D. $10$ cm.

PHẦN II. PHẦN TRẮC NGHIỆM ĐÚNG/ SAI (2,0 ĐIỂM)

Câu 21. Cho phương trình $x^2+(m-1)x-2=0$(1)

a. Phương trình vô nghiệm khi $m=1$

b. Với $\mathbf{m}\mathbf{=}\mathbf{0}$ , phương trình có nghiệm là ${\mathbf{x}}_{\mathbf{1}}\mathbf{=}\mathbf{-}\mathbf{1}\mathbf{;}{\mathbf{x}}_{\mathbf{2}}\mathbf{=}\mathbf{2}$.

c. Phương trình luôn có hai nghiệm dương với mọi giá trị m tùy ý.

d. Giả sử $x_1;x_2$ là hai nghiệm của pt (1) .Giá trị nhỏ nhất của biểu thức $A=x_1^2+x_2^2$ là $-2$ với $m=1$.

Câu 22: Gieo một đồng xu cân đối và đồng chất 3 lần liên tiếp. Kết quả của mỗi lần gieo có thể là ‘sấp” (S) hoặc “ngửa”. Biết rằng xác suất ra “sấp” hoặc “ngửa” là bằng nhau.

A. Xác suất để ba lần gieo đều là “sấp” (SSS) là $\frac{1}{3}$.

B. Xác suất để ba lần gieo có đúng hai lần “ngửa” một lần “sấp” là $\frac{3}{8}$.

C. Xác suất để ba lần gieo có ít nhất một lần “sấp” là $\frac{5}{8}$.

D. Xác suất để ba lần gieo có số lần “ngửa” nhiều hơn số lần “sấp” là nghiệm của phương trình $4x^2-4x+1=0$.

PHẦN III. TỰ LUẬN (3 điểm)

Câu 23 (0,5 điểm): Tìm $a$ để đồ thị hàm số $y=a{x}^2$ đi qua điểm $M(\sqrt{2};2).$

Câu 24 (1,0 điểm). Trong đợt giải phóng mặt bằng làm đường quốc lộ 10, gia đình bà Hạnh được đền bù một miếng đất hình chữ nhật có chiều dài hơn chiều rộng là 4 mét. Số tiền gia đình nhận được là 120 triệu đồng với giá 2 triệu đồng 1 mét vuông. Hãy tính kích thước của mảnh đất đó.

Câu 25 (1,5 điểm)

Cho nửa đường tròn (O) đường kính AB. Điểm M nằm trên nửa đường tròn (M ≠ A; B). Tiếp tuyến tại M cắt tiếp tuyến tại A và B của đường tròn (O) lần lượt tại C và D.

a. Chứng minh rằng: tứ giác ACMO nội tiếp.

b. Chứng minh rằng: $\widehat{CAM}=\widehat{ODM}$

c. Gọi P là giao điểm CD và AB Gọi E là giao điểm của AM và BD; F là giao điểm của AC và BM. Chứng minh: PA.PO = PC.PM và chứng minh: E; F; P thẳng hàng.

- Hết -

------------------------------------------

Mời bạn đọc tải tài liệu tham khảo đáp án chi tiết!