Đề thi tuyển sinh vào lớp 10 môn Toán năm học 2015-2016 Sở GD-ĐT TP Hồ Chí Minh
Đề thi tuyển sinh vào lớp 10 môn Toán
Sáng ngày 12/6/2015, Sở GD&ĐT TPHCM tổ chức thi tuyển sinh vào lớp 10 THPT môn Toán. VnDoc.com giới thiệu tới các bạn đề thi tuyển sinh vào lớp 10 môn Toán năm học 2015-2016 Sở GD-ĐT TP Hồ Chí Minh. Mời các bạn cùng tham khảo.
Tuyển tập đề thi vào lớp 10 môn Ngữ văn các tỉnh năm học 2014 - 2015
| SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ CHÍNH THỨC |
KỲ THI TUYỂN SINH LỚP 10 THPT TP.HCM Năm học: 2015 – 2016 MÔN: TOÁN Thời gian làm bài: 120 phút |
Bài 1: (2 điểm)
Giải các phương trình và hệ phương trình sau:
a) x2 - 8x + 15 = 0.
b) 2x2 - √2x - 2 = 0.
c) x4 - 5x2 - 6 = 0.
![]()
Bài 2: (1,5 điểm)
a) Vẽ đồ thị (P) của hàm số y = x2 và đường thẳng (D): y = x + 2 trên cùng một hệ trục toạ độ.
b) Tìm toạ độ các giao điểm của (P) và (D) ở câu trên bằng phép tính.
Bài 3: (1,5 điểm)
Thu gọn các biểu thức sau:
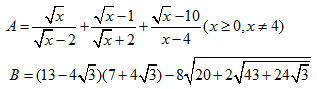
Bài 4: (1,5 điểm)
Cho phương trình x2 - mx + m - 2 = 0 (1) (x là ẩn số)
a) Chứng minh phương trình (1) luôn có 2 nghiệm phân biệt với mọi giá trị m
b) Định m để hai nghiệm x1, x2 của (1) thỏa mãn ![]()
Bài 5: (3,5 điểm)
Cho tam giác ABC (AB<AC) có ba góc nhọn. Đường tròn tâm O đường kính BC cắt các cạnh AC, AB lần lượt tại E, F. Gọi H là giao điểm của BE và CF. D là giao điểm của AH và BC.
a) Chứng minh: AD ┴ BC và AH.AD=AE.AC
b) Chứng minh EFDO là tứ giác nội tiếp
c) Trên tia đối của tia DE lấy điểm L sao cho DL = DF. Tính số đo góc BLC.
d) Gọi R, S lần lượt là hình chiếu của B, C lên EF. Chứng minh DE + DF = RS.
Đề thi tuyển sinh vào lớp 10 môn Ngữ văn năm học 2015-2016 Sở GD-ĐT TP Hồ Chí Minh
Đề thi tuyển sinh vào lớp 10 môn Toán năm học 2015-2016 Sở GD-ĐT Hà Nội
Đề thi tuyển sinh vào lớp 10 môn tiếng Anh năm học 2015-2016 Sở GD-ĐT TP. Hồ Chí Minh
Đáp án đề thi tuyển sinh vào lớp 10 môn Toán
Bài 1: (2 điểm)
Giải các phương trình và hệ phương trình sau:
a) x2 - 8x + 15 = 0.
Δ' = 42 - 15 = 1
↔ x = 4 + 1 = 5 hay x = 4 - 1 = 3
b) 2x2 - √2x - 2 = 0. (2)
Δ = 2 - 4(2)(-2) = 18
(2) ↔ x = (√2 + 3√2)/4 = √2 hay x = (√2 - 3√2)/4 = -√2/2
c) x4 - 5x2 - 6 = 0
Đặt u = x2 ≥ 0 pt thành:
u2 - 5u - 6 = 0 ↔ u = -1 (loại) hay u = 6
Do đó pt ↔ x2 = 6 ↔ x = ±√6.
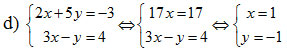
Bài 2:
a) Đồ thị:
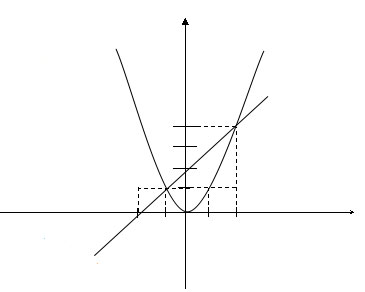
Lưu ý: (P) đi qua O(0; 0), (±1; 1); (±2; 4)
(D) đi qua (-1; 1), (2; 4)
b) PT hoành độ giao điểm của (P) và (D) là
x2 = x + 2 ↔ x2 - x - 2 = 0 ↔ x = -1 hay x = 2 (a-b+c=0)
y(-1) = 1, y(2) = 4
Vậy toạ độ giao điểm của (P) và (D) là (-1; 1), (2; 4).
Đề thi thử vào lớp 10 môn Ngữ văn thành phố Hà Nội năm học 2015-2016
Đề thi - Đáp án thi tuyển sinh lớp 10 THPT TP Hà Nội năm 2014 - 2015





