Cát tuyến là gì? Cát tuyến của đường tròn là gì?
Trong hình học lớp 9, cát tuyến là một khái niệm quan trọng, thường xuất hiện trong các bài toán liên quan đến đường tròn, tiếp tuyến và hình học phẳng. Vậy cát tuyến là gì? Cát tuyến của đường tròn có đặc điểm gì? Trong bài viết này, chúng ta sẽ cùng nhau tìm hiểu định nghĩa cát tuyến, cách xác định cát tuyến của đường tròn, và cách vận dụng vào các bài tập Toán lớp 9. Tài liệu được trình bày dễ hiểu, kèm ví dụ minh họa và lời giải chi tiết giúp học sinh nắm vững kiến thức và áp dụng hiệu quả vào thực hành. Dưới đây là nội dung chi tiết, các em tham khảo nhé.
Bài tập về Cát tuyến của đường tròn
1. Định nghĩa về cát tuyến
+ Cát tuyến là gì? Cát tuyến là một từ Hán - Việt. Trong đó “Cát” nghĩa là cắt, còn “tuyến” có nghĩa là đường thẳng. Bởi vậy, cát tuyến chính là một đường thẳng cắt các đường khác (đường thẳng, đường tròn, đường cong,…)
+ Theo khái niệm trong sách giáo khoa bộ môn toán, thì cát tuyến chính là một đường thẳng cắt một đường thẳng khác. Cát tuyến của đường tròn chính là 1 đường thẳng cắt đường tròn đó tại hai điểm phân biệt. Cát tuyến của 2 đường thẳng là 1 đường thẳng cắt 2 đường thẳng trên. Một vài trường hợp đặc biệt đó chính là cát tuyến đi qua tâm đường tròn.
+ Ứng dụng đường cát tuyến hình tròn
Đường cát tuyến hình tròn có thể được sử dụng để giải các bài toán liên quan đến tỉ lệ, tam giác đồng dạng, đường tròn nội tiếp và ngoại tiếp. Một số ví dụ về ứng dụng đường cát tuyến hình tròn là:
- Tính chiều cao của một ngọn núi khi biết góc nhìn từ hai điểm cách nhau một khoảng xác định.
- Tính bán kính của một đường tròn khi biết hai cát tuyến của nó và khoảng cách giữa hai điểm giao của chúng với đường tròn.
- Tính diện tích của một tứ giác nội tiếp trong một đường tròn khi biết các cạnh của nó và các góc tạo bởi các cát tuyến của chúng.
- Tính chiều dài của một cung tròn khi biết hai tiếp tuyến và một cát tuyến của nó
2. Tính chất của cát tuyến là gì toán 9?
Cho 1 đường tròn tâm O với 2 đường thẳng là AB và CD, ta có:
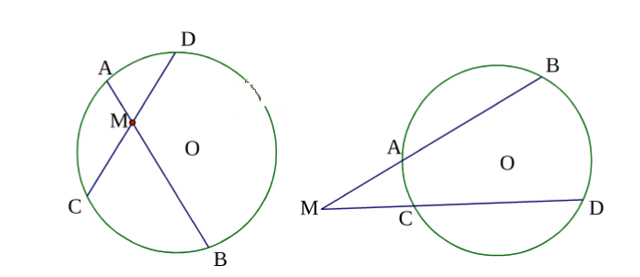
- Nếu 2 đường thẳng chứa các dây AB và CD của 1 đường tròn cắt nhau tại điểm M thì MA.MB = MC.MD
- Đảo lại, nếu 2 đường thẳng AB và CD cắt nhau tại điểm M và MA.MB = MC.MD thì 4 điểm A, B, C, D cũng sẽ thuộc cùng 1 đường tròn
- Nếu MC là tiếp tuyến, MAB là cát tuyến thì MC^2 = MA x MB = MO^2 – R^2
- Từ điểm K nằm bên ngoài đường tròn, ta kẻ lần lượt các tiếp tuyến KA, KB và cát tuyến KCD. Có H là trung điểm của CD thì 5 điểm K, H, A, B, O cùng nằm trên 1 trung điểm.
- Từ điểm K nằm ngoài đường tròn, ta kẻ các tiếp tuyến KA, KB với cát tuyến KCD đến đường tròn thì AC/AD = BC/BD. Ta có góc KAC = góc ADK => AC/AD = KC/KA.
3. Bài tập về cát tuyến đường tròn
Xem thêm phần Các bài toán về tiếp tuyến và cát tuyến (Có đáp án)
Bài tập 1: Từ điểm M nằm ngoài đường tròn (O) hãy vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA, MB đến đường tròn (O). Ở đây A, B là các tiếp điểm và C nằm giữa M, D.
a) CM: MA.MA = MC.MD.
b) Gọi I là trung điểm của CD. CMR: M, A, O, I, B cùng nằm trên 1 đường tròn.
c) Gọi H là giao điểm của AB và MO. Chứng minh rằng CHOD nội tiếp và AB là đường phân giác của góc CHD.
d) Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). CM: A, B, K thẳng hàng
Lời giải:
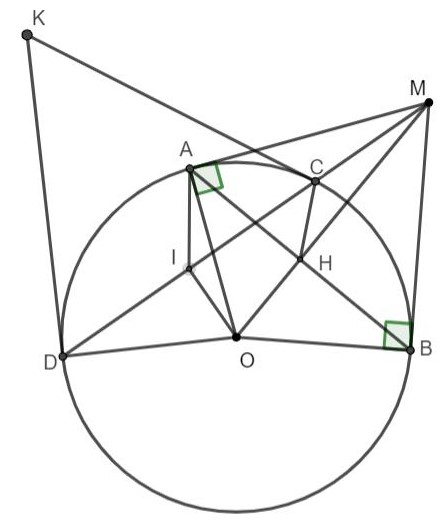
a) +) Có MA là tiếp tuyến của đường tròn (O) (giả thiết)
→ góc MAC = góc MDA → △ MAC ~ △ MDA (g.g)
→ ![]() \(\frac{{MA}}{{MD}} = \frac{{MC}}{{MA}}\) (cặp cạnh tương ứng tỉ lệ)
\(\frac{{MA}}{{MD}} = \frac{{MC}}{{MA}}\) (cặp cạnh tương ứng tỉ lệ)
→ MA2 = MC.MD (đpcm)
b) +) Có I là trung điểm của CD (giả thiết)
→ Góc MIO = 900 = góc MAO = MBO
→ 4 điểm M, A, O, I, B cùng thuộc đường tròn đường kính MO.
c) +) Có MA ⊥ OA, OM ⊥ AB tại H → MH. MO = MA2 = MC. MD
→ ![]() \(\frac{{MA}}{{MD}} = \frac{{MC}}{{MA}}\) → △ MHC ~ △ MDC → góc MHC = góc MDO
\(\frac{{MA}}{{MD}} = \frac{{MC}}{{MA}}\) → △ MHC ~ △ MDC → góc MHC = góc MDO
→ Tứ giác HCDO nội tiếp đường tròn
→ Góc OHD = góc OCD = góc ODC = góc MHC
→ 900 - góc MHC = 900 - góc OHD → góc CHB = góc BHD
→ HB là phân giác của góc CHD.
d) +) Có KC và KD là hai tiếp tuyến cắt nhau tại K của đường tròn (O)
→ Tứ giác KCOD nội tiếp đường tròn (hay 4 điểm K, C, O, D cùng thuộc một đường tròn)
mà tứ giác HODC nội tiếp đường tròn (chứng minh trên) (hay 4 điểm H, O, D, C cùng thuộc một đường tròn)
→ 5 điểm K, C, H, O, D cùng thuộc một đường tròn
→ HK là phân giác của góc CHD (do KC = KD)
→ 3 điểm A, B, K thẳng hàng.
Bài tập 2. Cho 2 đường thẳng song song a, b và một đường cát tuyến c. Hai tia phân giác của cặp góc trong cùng phía cắt nhau tại điểm I. Chứng minh điểm I cách đều 3 đường thẳng a, b và c.
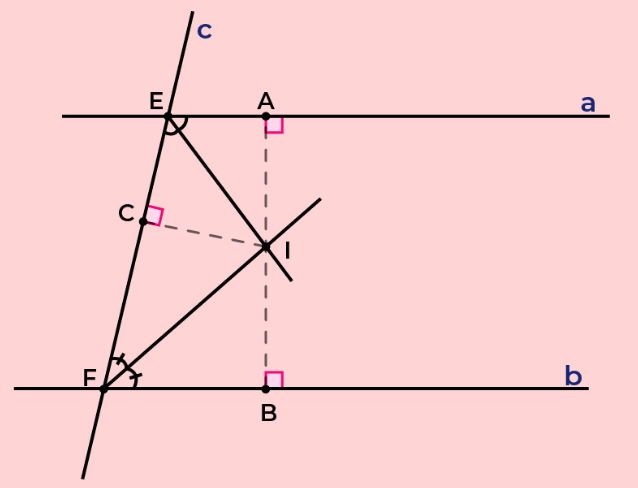
Bài giải
Gọi 3 điểm A, B, C lần lượt là chân đường vuông góc kẻ từ điểm I đến a, b, c.
Xét hai góc trong cùng phía CEA và CFB ta có:
Do I nằm trên tia phân giác của góc CEA nên IA = IC (1)
Do I nằm trên tia phân giác của góc CFB nên IC = IB (2)
Từ (1) và (2) => IA = IB = IC
=> I cách đều đường thẳng a, b và c.
Bài tập 3: Cho tam giác ![]() \(ABC\) có
\(ABC\) có ![]() \(\widehat{BAC}\) là góc nhỏ nhất trong ba góc của tam giác và nội tiếp đường tròn (O). Điểm
\(\widehat{BAC}\) là góc nhỏ nhất trong ba góc của tam giác và nội tiếp đường tròn (O). Điểm ![]() \(D\) thuộc cạnh
\(D\) thuộc cạnh ![]() \(BC\)sao cho
\(BC\)sao cho ![]() \(AD\) là phân giác
\(AD\) là phân giác ![]() \(\widehat{BAC}.\) Lấy các điểm
\(\widehat{BAC}.\) Lấy các điểm ![]() \(M,N\) thuộc (O) sao cho đường thẳng
\(M,N\) thuộc (O) sao cho đường thẳng ![]() \(CM,BN\)cùng song song với đường thẳng
\(CM,BN\)cùng song song với đường thẳng ![]() \(AD\)
\(AD\)
1. Chứng minh rằng ![]() \(AM = AN\)
\(AM = AN\)
2. Gọi giao điểm của đường thẳng ![]() \(MN\) với các đường thẳng
\(MN\) với các đường thẳng ![]() \(AC, A B\) lần lượt là
\(AC, A B\) lần lượt là ![]() \(E,F.\) Chứng minh rằng bốn điểm
\(E,F.\) Chứng minh rằng bốn điểm ![]() \(B,C,E,F\) cùng thuộc một đường tròn
\(B,C,E,F\) cùng thuộc một đường tròn
3. Gọi ![]() \(P,Q\) theo thứ tự là trung điểm của các đoạn thẳng
\(P,Q\) theo thứ tự là trung điểm của các đoạn thẳng ![]() \(AM,AN.\) Chứng minh rằng các đường thẳng
\(AM,AN.\) Chứng minh rằng các đường thẳng ![]() \(EQ,FP,AD\) đồng quy.
\(EQ,FP,AD\) đồng quy.
Hướng dẫn giải

1. Chứng minh rằng ![]() \(AM = AN\)
\(AM = AN\)
Ta có: ![]() \(\widehat{NBA} =
\widehat{DAB}\)(so le trong do
\(\widehat{NBA} =
\widehat{DAB}\)(so le trong do ![]() \(BN//AD)\)
\(BN//AD)\)
![]() \(\widehat{DAB} =\widehat{DAC}(gt)\);
\(\widehat{DAB} =\widehat{DAC}(gt)\);![]() \(\widehat{DAC} =
\widehat{ACM}\)(so le trong do
\(\widehat{DAC} =
\widehat{ACM}\)(so le trong do ![]() \(CM//AD)\)
\(CM//AD)\)
![]() \(\Rightarrow \widehat{NBA} = \widehat{MCA}
\Rightarrow sd\widehat{AN} = sd\widehat{AM}\)(trong một đường tròn, hai góc nội tiếp bằng nhau thì chắn hai cung bằng nhau).
\(\Rightarrow \widehat{NBA} = \widehat{MCA}
\Rightarrow sd\widehat{AN} = sd\widehat{AM}\)(trong một đường tròn, hai góc nội tiếp bằng nhau thì chắn hai cung bằng nhau).
Vậy ![]() \(AM = AN\)(trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau)
\(AM = AN\)(trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau)
2. Chứng minh rằng 4 điểm ![]() \(B,C,E,F\)cùng thuộc một đường tròn.
\(B,C,E,F\)cùng thuộc một đường tròn.
Ta có: ![]() \(\widehat{AEF} = \frac{1}{2}\left(
sd\widehat{AN} + sd\widehat{CM} \right)\)(góc có đỉnh ở bên trong đường tròn)
\(\widehat{AEF} = \frac{1}{2}\left(
sd\widehat{AN} + sd\widehat{CM} \right)\)(góc có đỉnh ở bên trong đường tròn)
![]() \(= \frac{1}{2}\left( sd\widehat{AM} +
sd\widehat{CM} \right) = \frac{1}{2}sd\widehat{AC} =
\widehat{ABC}\)(góc nội tiếp bằng nửa số đo cung bị chắn)
\(= \frac{1}{2}\left( sd\widehat{AM} +
sd\widehat{CM} \right) = \frac{1}{2}sd\widehat{AC} =
\widehat{ABC}\)(góc nội tiếp bằng nửa số đo cung bị chắn)
Vậy tứ giác ![]() \(BCEF\) là tứ giác nội tiếp (tứ giác có góc ngoài và góc trong tại đỉnh đối diện bằng nhau) hay
\(BCEF\) là tứ giác nội tiếp (tứ giác có góc ngoài và góc trong tại đỉnh đối diện bằng nhau) hay ![]() \(B,C,E, F\)cùng thuộc một đường tròn.
\(B,C,E, F\)cùng thuộc một đường tròn.
3. Chứng minh các đường thẳng ![]() \(EQ,FP,AD\)đồng quy
\(EQ,FP,AD\)đồng quy
Áp dụng định lý Mê-lê-na-uýt trong tam giác ![]() \(AHN,\)cát tuyến
\(AHN,\)cát tuyến ![]() \(EKQ\), ta có:
\(EKQ\), ta có:
![]() \(\frac{EN}{EH}.\frac{KH}{KA}.\frac{QA}{QN}
= 1 \Rightarrow \frac{EN}{EH}.\frac{KH}{KA} = 1\)(do
\(\frac{EN}{EH}.\frac{KH}{KA}.\frac{QA}{QN}
= 1 \Rightarrow \frac{EN}{EH}.\frac{KH}{KA} = 1\)(do ![]() \(Q\) là trung điểm của
\(Q\) là trung điểm của ![]() \(AN(gt)\) nên
\(AN(gt)\) nên ![]() \(QA
= QN)\)
\(QA
= QN)\)
![]() \(\Rightarrow \frac{EN}{EH} =
\frac{KA}{KH}(I)\)
\(\Rightarrow \frac{EN}{EH} =
\frac{KA}{KH}(I)\)
Gọi  \(AD \cap PE = \left\{ K'
\right\}.\)Ta đi chứng minh
\(AD \cap PE = \left\{ K'
\right\}.\)Ta đi chứng minh  \(K'
\equiv K\)
\(K'
\equiv K\)
Áp dụng định lý Mê-lê-na-uýt trong tam giác ![]() \(AHM,\)cát tuyến
\(AHM,\)cát tuyến ![]() \(PKF\) ta có:
\(PKF\) ta có:
 \(\frac{FM}{FH}.\frac{K'H}{K'A}.\frac{PA}{PM}
= 1 \Rightarrow \frac{FM}{FH}.\frac{K'H}{K'A} = 1\)(Do
\(\frac{FM}{FH}.\frac{K'H}{K'A}.\frac{PA}{PM}
= 1 \Rightarrow \frac{FM}{FH}.\frac{K'H}{K'A} = 1\)(Do ![]() \(P\) là trung điểm của
\(P\) là trung điểm của ![]() \(AM(gt)\) nên
\(AM(gt)\) nên ![]() \(PA
= PM)\)
\(PA
= PM)\)
 \(\Rightarrow \frac{FM}{FH} =
\frac{K'A}{K'H}(II)\)
\(\Rightarrow \frac{FM}{FH} =
\frac{K'A}{K'H}(II)\)
Ta sẽ chứng minh ![]() \(\frac{EN}{EH} =
\frac{FM}{FH} \Leftrightarrow \frac{FM}{EN} = \frac{FH}{EH} = \frac{FM -
FH}{EN - EH} = \frac{HM}{HN}(*)\)(tính chất dãy tỉ số bằng nhau)
\(\frac{EN}{EH} =
\frac{FM}{FH} \Leftrightarrow \frac{FM}{EN} = \frac{FH}{EH} = \frac{FM -
FH}{EN - EH} = \frac{HM}{HN}(*)\)(tính chất dãy tỉ số bằng nhau)
Vì ![]() \(BN//AD//CM\)nên áp dụng định lý Ta – let ta có:
\(BN//AD//CM\)nên áp dụng định lý Ta – let ta có: ![]() \(\frac{HM}{HN} =
\frac{DC}{DB}\)
\(\frac{HM}{HN} =
\frac{DC}{DB}\)
Lại có : ![]() \(\frac{DC}{DB} =
\frac{AC}{AB}\)(định lý đường phân giác), do đó:
\(\frac{DC}{DB} =
\frac{AC}{AB}\)(định lý đường phân giác), do đó: ![]() \(\frac{HM}{HN} = \frac{AC}{AB}(1)\)
\(\frac{HM}{HN} = \frac{AC}{AB}(1)\)
Xét ![]() \(\Delta AEF\)và
\(\Delta AEF\)và ![]() \(\Delta ABC\)có:
\(\Delta ABC\)có: ![]() \(\widehat{AEF} =
\widehat{ABC}(cmt),\widehat{BAC}\) chung
\(\widehat{AEF} =
\widehat{ABC}(cmt),\widehat{BAC}\) chung
![]() \(\Rightarrow \Delta AEF\sim\Delta
ABC(g.g) \Rightarrow \frac{AC}{AB} = \frac{AF}{AE}(2)\)
\(\Rightarrow \Delta AEF\sim\Delta
ABC(g.g) \Rightarrow \frac{AC}{AB} = \frac{AF}{AE}(2)\)
Từ (1) và (2)![]() \(\Rightarrow \frac{HM}{HN} =
\frac{AF}{AE}(3)\)
\(\Rightarrow \frac{HM}{HN} =
\frac{AF}{AE}(3)\)
Tiếp tục áp dụng định lý đường phân giác trong tam giác ![]() \(AEF\) ta có:
\(AEF\) ta có: ![]() \(\frac{AF}{AE} = \frac{HF}{HE}(4)\)
\(\frac{AF}{AE} = \frac{HF}{HE}(4)\)
Từ (3) và (4) ta suy ra ![]() \(\frac{HM}{HN} =
\frac{HF}{HE},\)do đó
\(\frac{HM}{HN} =
\frac{HF}{HE},\)do đó ![]() \((*)\)được chứng minh, tức là
\((*)\)được chứng minh, tức là ![]() \(\frac{EN}{EH} = \frac{FM}{FH}(III)\)
\(\frac{EN}{EH} = \frac{FM}{FH}(III)\)
Từ ![]() \((I),(II),(III)\)suy ra
\((I),(II),(III)\)suy ra  \(\frac{KA}{KH} = \frac{K'A}{K'H}\), do đó
\(\frac{KA}{KH} = \frac{K'A}{K'H}\), do đó  \(K \equiv K'\)
\(K \equiv K'\)
Vậy ![]() \(EQ,FP,AD\) đồng quy tại K
\(EQ,FP,AD\) đồng quy tại K
Bài tập 4. Cho điểm A nằm ngoài đường tròn (O). Từ A kẻ hai tiếp tuyến AB, AC và cát tuyến ADE không đi qua tâm tới đường tròn đó (B; C là hai tiếp điểm, D nằm giữa A và E). Gọi H là giao điểm của AO và BC
a. Chứng minh tứ giác ABOC là tứ giác nội tiếp
b. Chứng minh AH . AO = AD. AE
c. Tiếp tuyến tại D của đường tròn (O) cắt AB, AC theo thứ tự tại I; K. Qua điểm O kẻ đường thẳng vuông góc với OA cắt AB tại P và cắt AC tại Q. Chứng minh rằng : ![]() \(IP + KQ \geq
PQ\).
\(IP + KQ \geq
PQ\).
Hướng dẫn giải
Hình vẽ minh họa

a. Chứng minh ABOC là tứ giác nội tiếp
Ta có: ![]() \(\widehat{B} + \widehat{C} = 90^{0}
+ 90^{0} = 180^{0}\) là tứ giác nội tiếp
\(\widehat{B} + \widehat{C} = 90^{0}
+ 90^{0} = 180^{0}\) là tứ giác nội tiếp
b. Chứng minh AH . AO = AD. AE
Xét ACD và AEC có:
Góc A chung
![]() \(\widehat{ACD} =
\widehat{AEC}\)(cùng chắn cung CD)
\(\widehat{ACD} =
\widehat{AEC}\)(cùng chắn cung CD)
![]() \(\Rightarrow \Delta ACD\sim\Delta AEC(g -
g) \Rightarrow \frac{AC}{AE} = \frac{AD}{AC} \Rightarrow AE.AD =
AC^{2}(*)\)
\(\Rightarrow \Delta ACD\sim\Delta AEC(g -
g) \Rightarrow \frac{AC}{AE} = \frac{AD}{AC} \Rightarrow AE.AD =
AC^{2}(*)\)
Áp dụng hệ thức lượng ta có: ![]() \(AH.AO =
AC^{2}\ \ (2)\)
\(AH.AO =
AC^{2}\ \ (2)\)
Từ (1) và (2) ![]() \(\Rightarrow AH.AO =
AD.AE\)
\(\Rightarrow AH.AO =
AD.AE\)
c. Chứng minh rằng: ![]() \(IP + KQ \geq
PQ\)
\(IP + KQ \geq
PQ\)
![]() \(\widehat{PIK} + \widehat{IKQ} +\widehat{P} + \widehat{Q} = 360^{0}\)
\(\widehat{PIK} + \widehat{IKQ} +\widehat{P} + \widehat{Q} = 360^{0}\)
![]() \(\Rightarrow 2\widehat{PIK} +
2\widehat{OKQ} + 2\widehat{P} = 360^{0}\)
\(\Rightarrow 2\widehat{PIK} +
2\widehat{OKQ} + 2\widehat{P} = 360^{0}\)
![]() \(\Rightarrow \widehat{PIK} +
\widehat{OKQ} + \widehat{P} = 180^{0}\)
\(\Rightarrow \widehat{PIK} +
\widehat{OKQ} + \widehat{P} = 180^{0}\)
Lại có: ![]() \(\widehat{PIO} + \widehat{IOP} +
\widehat{P} = 180^{0} \Rightarrow \widehat{OKQ} =
\widehat{IOP}\)
\(\widehat{PIO} + \widehat{IOP} +
\widehat{P} = 180^{0} \Rightarrow \widehat{OKQ} =
\widehat{IOP}\)
Xét tam giác PIO và QOK có:
 \(\left\{ \begin{matrix}
\widehat{OKQ} = \widehat{IOP} \\
\widehat{OKQ} = \widehat{IPO} \\
\end{matrix} \right.\ \Rightarrow \Delta QOK\sim\Delta OIP(g -
g)\)
\(\left\{ \begin{matrix}
\widehat{OKQ} = \widehat{IOP} \\
\widehat{OKQ} = \widehat{IPO} \\
\end{matrix} \right.\ \Rightarrow \Delta QOK\sim\Delta OIP(g -
g)\)
![]() \(\Rightarrow \frac{PI}{QO} =
\frac{PO}{QK} \Rightarrow PI.QK = PO.QO = OP^{2}\)
\(\Rightarrow \frac{PI}{QO} =
\frac{PO}{QK} \Rightarrow PI.QK = PO.QO = OP^{2}\)
Áp dụng bất đẳng thức Cô – si ta có:
![]() \(IP + KQ \geq 2\sqrt{IP.KQ} =
2\sqrt{OP^{2}} = PQ\)
\(IP + KQ \geq 2\sqrt{IP.KQ} =
2\sqrt{OP^{2}} = PQ\)
Vậy ![]() \(IP + KQ \geq PQ\)
\(IP + KQ \geq PQ\)
Bài tập 5: Cho đường tròn (O; R), từ một điểm A trên (O) kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điểm M bất kì ( M khác A) kẻ cát tuyến MNP và gọi K là trung điểm của NP, kẻ tiếp tuyến MB (B là tiếp điểm). Kẻ AC ⊥ MB, BD ⊥ MA, gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB.
1.Chứng minh tứ giác AMBO nội tiếp.
2.Chứng minh năm điểm O, K, A, M, B cùng nằm trên một đường tròn .
3.Chứng minh OI.OM = R2; OI. IM = IA2.
4.Chứng minh OAHB là hình thoi.
5.Chứng minh ba điểm O, H, M thẳng hàng.
6. Tìm quỹ tích của điểm H khi M di chuyển trên đường thẳng d
Lời giải:
1. (HS tự làm).
2. Vì K là trung điểm NP nên OK ⊥ NP ( quan hệ đường kính
Hình vẽ minh họa
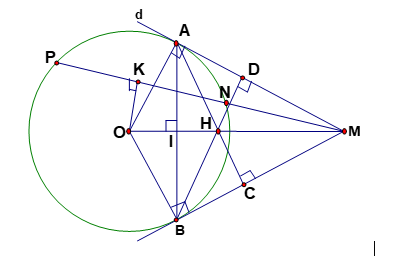
Và dây cung) => ∠OKM = 900. Theo tính chất tiếp tuyến ta có ∠OAM = 900; ∠OBM = 900. như vậy K, A, B cùng nhìn OM dưới một góc 900 nên cùng nằm trên đường tròn đường kính OM.
Vậy năm điểm O, K, A, M, B cùng nằm trên một đường tròn.
3. Ta có MA = MB ( t/c hai tiếp tuyến cắt nhau); OA = OB = R
=> OM là trung trực của AB => OM ⊥ AB tại I .
Theo tính chất tiếp tuyến ta có ∠OAM = 900 nên tam giác OAM vuông tại A có AI là đường cao.
Áp dụng hệ thức giữa cạnh và đường cao => OI.OM = OA2 hay OI.OM = R2; và OI. IM = IA2.
4. Ta có OB ⊥ MB (tính chất tiếp tuyến) ; AC ⊥ MB (gt) => OB // AC hay OB // AH.
OA ⊥ MA (tính chất tiếp tuyến) ; BD ⊥ MA (gt) => OA // BD hay OA // BH.
=> Tứ giác OAHB là hình bình hành; lại có OA = OB (=R) => OAHB là hình thoi.
5. Theo trên OAHB là hình thoi. => OH ⊥ AB; cũng theo trên OM ⊥ AB => O, H, M thẳng hàng( Vì qua O chỉ có một đường thẳng vuông góc với AB).
6. (HD) Theo trên OAHB là hình thoi. => AH = AO = R. Vậy khi M di động trên d thì H cũng di động nhưng luôn cách A cố định một khoảng bằng R. Do đó quỹ tích của điểm H khi M di chuyển trên đường thẳng d là nửa đường tròn tâm A bán kính AH = R
Bài tập 6. Cho ba điểm  \(J,I,J'\) cùng nằm trên 1 đường thẳng theo thứ tự đó. Cho biết
\(J,I,J'\) cùng nằm trên 1 đường thẳng theo thứ tự đó. Cho biết ![]() \(IJ = 10\text{
}cm\),
\(IJ = 10\text{
}cm\),  \(IJ' = 4cm\). Vẽ đường tròn
\(IJ' = 4cm\). Vẽ đường tròn ![]() \((O)\) đường kính
\((O)\) đường kính ![]() \(IJ\) và đường tròn
\(IJ\) và đường tròn  \(\left( O' \right)\) đường kính
\(\left( O' \right)\) đường kính  \(IJ'\).
\(IJ'\).
a) Chứng minh ![]() \((O)\) và
\((O)\) và  \(\left( O' \right)\) tiếp xúc ngoài ở
\(\left( O' \right)\) tiếp xúc ngoài ở ![]() \(I\).
\(I\).
b) Gọi ![]() \(A\) là 1 điểm trên đường tròn
\(A\) là 1 điểm trên đường tròn ![]() \((O)\), tia
\((O)\), tia ![]() \(AI\) cắt
\(AI\) cắt  \(\left(
O' \right)\) ở
\(\left(
O' \right)\) ở  \(A'\). Chứng minh rằng
\(A'\). Chứng minh rằng  \(\bigtriangleup AIJ \sim
\Delta A'IJ'\).
\(\bigtriangleup AIJ \sim
\Delta A'IJ'\).
c) Qua điểm ![]() \(I\) kẻ 1 cát tuyến cắt
\(I\) kẻ 1 cát tuyến cắt ![]() \((O)\) ở
\((O)\) ở ![]() \(B\) (
\(B\) ( ![]() \(B\) và
\(B\) và ![]() \(A\) thuộc hai nửa mặt phẳng bờ
\(A\) thuộc hai nửa mặt phẳng bờ ![]() \(IJ\) ), cắt đường tròn
\(IJ\) ), cắt đường tròn  \(\left( O' \right)\) ở
\(\left( O' \right)\) ở  \(B'\). Chứng minh:
\(B'\). Chứng minh:  \(\bigtriangleup IAB^{\circ} \backsim \bigtriangleup
IA'B'\).
\(\bigtriangleup IAB^{\circ} \backsim \bigtriangleup
IA'B'\).
d) Chứng minh rằng:  \(\bigtriangleup OAB
\backsim \bigtriangleup OA'B'\).
\(\bigtriangleup OAB
\backsim \bigtriangleup OA'B'\).
e) Tứ giác  \(ABA'B'\) là hình gì vì sao?
\(ABA'B'\) là hình gì vì sao?
Hướng dẫn giải
Hình vẽ minh họa:
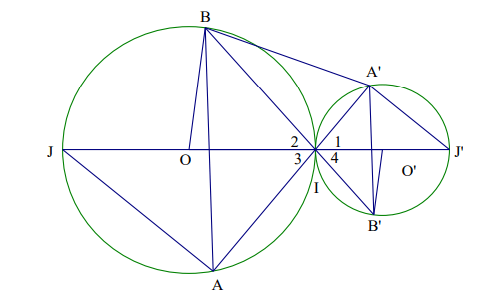
a) Ta có:  \(OO' = OI +
O'I\). Vậy Hai đường tròn tiếp xúc ngoài tại
\(OO' = OI +
O'I\). Vậy Hai đường tròn tiếp xúc ngoài tại ![]() \(I\)
\(I\)
b) Xét ![]() \(\bigtriangleup AIJ\) và
\(\bigtriangleup AIJ\) và  \(\Delta A'IJ'\) có:
\(\Delta A'IJ'\) có:  \(\left\{ \begin{matrix}
\widehat{A} = {\widehat{A}}' = 90^{0} \\
{\widehat{I}}_{1} = {\widehat{I}}_{2}
\end{matrix} \Rightarrow \Delta AII \backsim \Delta A'IJ'
\right.\)
\(\left\{ \begin{matrix}
\widehat{A} = {\widehat{A}}' = 90^{0} \\
{\widehat{I}}_{1} = {\widehat{I}}_{2}
\end{matrix} \Rightarrow \Delta AII \backsim \Delta A'IJ'
\right.\)
c)  \(\bigtriangleup AII \backsim
\bigtriangleup A'IJ'(g - g)\)
\(\bigtriangleup AII \backsim
\bigtriangleup A'IJ'(g - g)\)
 \(\Rightarrow \frac{IA}{IA'} =
\frac{IJ}{JI'} = \frac{10}{4} = \frac{5}{2}\) (1)
\(\Rightarrow \frac{IA}{IA'} =
\frac{IJ}{JI'} = \frac{10}{4} = \frac{5}{2}\) (1)
 \(\Delta OIB \backsim \Delta
O'IB'(g - g) \Rightarrow
\frac{\frac{OB}{}}{O'B'}\)
\(\Delta OIB \backsim \Delta
O'IB'(g - g) \Rightarrow
\frac{\frac{OB}{}}{O'B'}\)
 \(\Rightarrow \widehat{B_{1}} =
\widehat{B_{1}'} \Rightarrow \frac{IB}{IB'} =
\frac{OB}{O'B'} = \frac{5}{2}\) (2)
\(\Rightarrow \widehat{B_{1}} =
\widehat{B_{1}'} \Rightarrow \frac{IB}{IB'} =
\frac{OB}{O'B'} = \frac{5}{2}\) (2)
Từ (1)(2)  \(\Rightarrow \frac{IA}{IA'}
= \frac{IB}{IB'} = \frac{5}{2};\widehat{AIB} =
\widehat{A'IB}\)
\(\Rightarrow \frac{IA}{IA'}
= \frac{IB}{IB'} = \frac{5}{2};\widehat{AIB} =
\widehat{A'IB}\)
 \(\Rightarrow \bigtriangleup IAB \backsim
\bigtriangleup IA'B'(c - g - c)\)
\(\Rightarrow \bigtriangleup IAB \backsim
\bigtriangleup IA'B'(c - g - c)\)
d) Chứng minh  \(\bigtriangleup IAB^{\circ}
\backsim \bigtriangleup IA'B'(c - g - c)\)
\(\bigtriangleup IAB^{\circ}
\backsim \bigtriangleup IA'B'(c - g - c)\)
 \(\Rightarrow \frac{AB}{A'B'} =
\frac{IA}{IA'} = \frac{5}{2}\) mà
\(\Rightarrow \frac{AB}{A'B'} =
\frac{IA}{IA'} = \frac{5}{2}\) mà  \(\frac{OA}{O'A'} = \frac{OB}{O'B'}
= \frac{5}{2}\)
\(\frac{OA}{O'A'} = \frac{OB}{O'B'}
= \frac{5}{2}\)
 \(\Rightarrow \frac{OA}{O'A'} =
\frac{OB}{O'B'} = \frac{AB}{A'B'}\)
\(\Rightarrow \frac{OA}{O'A'} =
\frac{OB}{O'B'} = \frac{AB}{A'B'}\)
 \(\Rightarrow \bigtriangleup AOB \backsim
\bigtriangleup A'O'B'\)
\(\Rightarrow \bigtriangleup AOB \backsim
\bigtriangleup A'O'B'\)
e) Ta có:  \(\bigtriangleup AOB^{\circ}
\bigtriangleup A'O'B'\)
\(\bigtriangleup AOB^{\circ}
\bigtriangleup A'O'B'\)
![]() \(\Rightarrow \widehat{OBA} =\widehat{O'B'A'};\widehat{OBI} = \widehat{ O'B'I'}\)
\(\Rightarrow \widehat{OBA} =\widehat{O'B'A'};\widehat{OBI} = \widehat{ O'B'I'}\)
 \(\Rightarrow \widehat{ABI} =
\widehat{AB'I'} \Rightarrow AB//A'B'\).
\(\Rightarrow \widehat{ABI} =
\widehat{AB'I'} \Rightarrow AB//A'B'\).
Bài tập 6. Cho đường tròn ![]() \((O;5\text{
}cm)\). Cát tuyến qua
\((O;5\text{
}cm)\). Cát tuyến qua ![]() \(A\) ở ngoài
\(A\) ở ngoài ![]() \((O)\) cắt
\((O)\) cắt ![]() \((O)\) tại
\((O)\) tại ![]() \(B\) và
\(B\) và ![]() \(C\). Cho biết
\(C\). Cho biết ![]() \(AB = BC\) và kẻ đường kính
\(AB = BC\) và kẻ đường kính ![]() \(COD\). Độ dài đoạn thẳng
\(COD\). Độ dài đoạn thẳng ![]() \(AD\) bằng bao nhiêu centimet?
\(AD\) bằng bao nhiêu centimet?
Hướng dẫn giải
Hình vẽ minh họa:
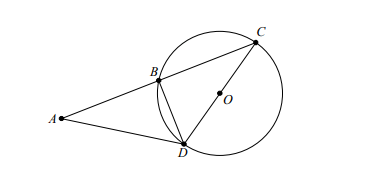
Xét ( ![]() \(O\) ) có
\(O\) ) có ![]() \(OB = OC = OD\) suy ra
\(OB = OC = OD\) suy ra ![]() \(BO = \frac{DC}{2}\) hay
\(BO = \frac{DC}{2}\) hay ![]() \(\bigtriangleup BDC\) vuông tại
\(\bigtriangleup BDC\) vuông tại ![]() \(B\) (tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông).
\(B\) (tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông).
Suy ra ![]() \(BD\bot AC\).
\(BD\bot AC\).
![]() \(\bigtriangleup ABD = \bigtriangleup
CBD\) nên
\(\bigtriangleup ABD = \bigtriangleup
CBD\) nên ![]() \(DA = DC = 2R = 10\text{
}cm\).
\(DA = DC = 2R = 10\text{
}cm\).
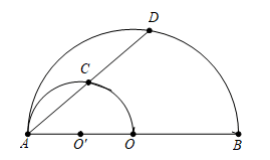
Bài tập 7. Cho nửa đường tròn ![]() \((O)\), đường kính
\((O)\), đường kính ![]() \(AB\). Vẽ nưa đường tròn tâm
\(AB\). Vẽ nưa đường tròn tâm  \(O'\) đường kính
\(O'\) đường kính ![]() \(AO\) (cùng phía với nửa đường tròn
\(AO\) (cùng phía với nửa đường tròn ![]() \((O)\) ). Một cát tuyến bất kỳ qua
\((O)\) ). Một cát tuyến bất kỳ qua ![]() \(A\) cắt
\(A\) cắt  \(\left(
O' \right);(O)\) lần lượt tại
\(\left(
O' \right);(O)\) lần lượt tại ![]() \(C,D\). Chọn khẳng định sai?
\(C,D\). Chọn khẳng định sai?
A. ![]() \(C\) là trung điểm của
\(C\) là trung điểm của ![]() \(AD\).
\(AD\).
B. Các tiếp tuyến tại ![]() \(C\) và
\(C\) và ![]() \(D\) của các nửa đường tròn song song với nhau.
\(D\) của các nửa đường tròn song song với nhau.
C.  \(O'C//OD\).
\(O'C//OD\).
D. Các tiếp tuyến tại ![]() \(C\) và
\(C\) và ![]() \(D\) của các nưa đường tròn cắt nhau.
\(D\) của các nưa đường tròn cắt nhau.
Hướng dẫn giải
Hình vẽ minh họa:
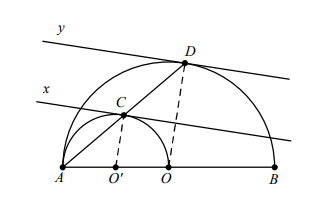
Xét đường tròn  \(\left( O'
\right)\) có
\(\left( O'
\right)\) có ![]() \(OA\) là đường kính và
\(OA\) là đường kính và  \(C \in \left( O' \right)\) nên
\(C \in \left( O' \right)\) nên ![]() \(\widehat{ACO} = 90^{\circ} \Rightarrow
AD\bot CO\)
\(\widehat{ACO} = 90^{\circ} \Rightarrow
AD\bot CO\)
Xét đường tròn ![]() \((O)\) có
\((O)\) có ![]() \(OA = OD \Rightarrow \bigtriangleup OAD\) cân tại
\(OA = OD \Rightarrow \bigtriangleup OAD\) cân tại ![]() \(O\) có
\(O\) có ![]() \(OC\) là đường cao nên
\(OC\) là đường cao nên ![]() \(OC\) cũng là đường trung tuyến hay
\(OC\) cũng là đường trung tuyến hay ![]() \(C\) là trung điểm của
\(C\) là trung điểm của ![]() \(AD\).
\(AD\).
Xét tam giác ![]() \(AOD\) có
\(AOD\) có  \(O'C\) là đường trung bình nên
\(O'C\) là đường trung bình nên  \(O'C//OD\)
\(O'C//OD\)
Kẻ các tiếp tuyến ![]() \(Cx;Dy\) với các nưa đường tròn ta có
\(Cx;Dy\) với các nưa đường tròn ta có  \(Cx\bot O'C;Dy\bot
OD\) mà
\(Cx\bot O'C;Dy\bot
OD\) mà  \(O'C//OD\) nên
\(O'C//OD\) nên ![]() \(Cx\bot Dy\).
\(Cx\bot Dy\).
Do đó phương án ![]() \(A,B,C\) đúng.
\(A,B,C\) đúng.
Tứ giác  \(ABA'B'\) có hai cạnh đối song song vậy là hình thang.
\(ABA'B'\) có hai cạnh đối song song vậy là hình thang.
----------------------------------------------------------------
Hiểu rõ khái niệm cát tuyến, đặc biệt là cát tuyến của đường tròn, sẽ giúp học sinh lớp 9 giải quyết tốt các bài toán liên quan đến đường tròn, tam giác, tứ giác nội tiếp và các dạng toán chứng minh hình học. Đây cũng là nền tảng kiến thức quan trọng để học tốt chương trình hình học lớp 10 và các lớp cao hơn. Hãy luyện tập nhiều dạng bài, kết hợp với việc học lý thuyết một cách logic để ghi nhớ lâu hơn và xử lý linh hoạt trong các tình huống đề thi. Đừng quên lưu bài viết để ôn lại khi cần và chia sẻ cho bạn bè cùng học nhé!









