Chứng minh biểu thức lượng giác Toán 9
Hướng dẫn chi tiết cách chứng minh biểu thức lượng giác Toán 9
Trong chương trình Toán 9, chuyên đề hệ thức lượng trong tam giác vuông giữ vai trò quan trọng trong việc rèn luyện tư duy logic và kỹ năng biến đổi đại số. Một trong những dạng bài tập tiêu biểu là chứng minh biểu thức lượng giác, giúp học sinh củng cố kiến thức về các tỉ số lượng giác của góc nhọn và vận dụng linh hoạt các công thức để xử lý các bài toán khó. Bài viết này sẽ hướng dẫn chi tiết cách tiếp cận, các phương pháp thường dùng và cung cấp bài tập minh họa có lời giải để học sinh nắm chắc kiến thức, tự tin ôn tập và áp dụng vào các kỳ thi.
Bài tập 1. Cho tam giác ABC vuông tại A. Chứng minh rằng 
\(\tan\frac{\widehat{ABC}}{2} = \frac{AC}{AB +
BC}\).
Hướng dẫn giải
Hình vẽ minh họa
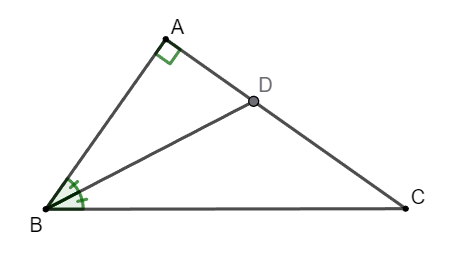
Vẽ đường phân giác BD của \(\Delta\)ABC (D \(\in\) AC).
Theo tính chất đường phân giác của tam giác ta có:
\(\frac{AD}{DC} = \frac{AB}{BC}
\Leftrightarrow \frac{AD}{AB} = \frac{DC}{BC}\)
\(\Rightarrow \frac{AD}{AB} = \frac{AD +
DC}{AB + BC} \Rightarrow \frac{AD}{AB} = \frac{AC}{AB +
BC}\).
Xét \(\Delta\)ABD có \(\widehat{BAD} = 90^0\) \(\Rightarrow \tan\widehat{ABD} =
\frac{AD}{AB}\)
\(\Leftrightarrow
\tan\frac{\widehat{ABC}}{2} = \frac{AC}{AB + BC}\)
Vậy \(\tan\frac{\widehat{ABC}}{2} =
\frac{AC}{AB + BC}\).
Bài tập 2. Chứng minh định lí sin: Trong một tam giác nhọn, độ dài các cạnh tỉ lệ với sin của các góc đối diện: \(\frac{a}{\sin A} = \frac{b}{\sin B} =
\frac{c}{\sin C}\).
Hướng dẫn giải
* Phương pháp giải
Để có sin A (hoặc sin B, sin C) thì phải xét tam giác vuông với A là một góc nhọn. Do đó phải vẽ thêm đường cao.
* Trình bày lời giải:
Hình vẽ minh họa
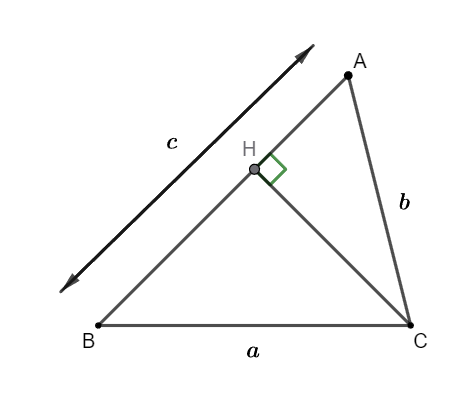
Vẽ đường cao CH.
Xét ∆ACH vuông tại H ta có: \(\sin A =
\frac{CH}{AC}\) (1)
Xét ∆BCH vuông tại H ta có: \(\sin B =
\frac{CH}{BC}\) (2)
Từ (1) và (2) suy ra \(\frac{\sin A}{\sin
B} = \frac{CH}{AC}:\frac{CH}{BC} = \frac{BC}{AC} = \frac{a}{b}\) .
Do đó \(\frac{a}{\sin A} = \frac{b}{\sin
B}\)
Chứng minh tương tự ta được \(\frac{b}{\sin
B} = \frac{c}{\sin C}\)
Vậy \(\frac{a}{\sin A} = \frac{b}{\sin B} =
\frac{c}{\sin C}\).
Bài tập 3. Cho tam giác \(ABC\) có trực tâm \(H\) là trung điểm của đường cao \(AD\). Chứng minh: \(\cos A = \cos B.cosC\).
Hướng dẫn giải
Hình vẽ minh họa
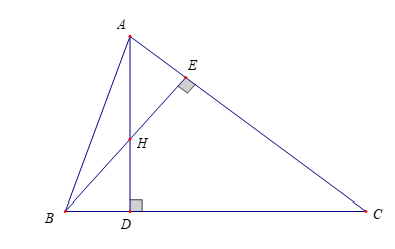
Ta có
\(\cos A = \frac{AE}{AB};\cos B.\cos C =\frac{BD}{AB}.\frac{DC}{AC}\ \ \ \ (1)\)
Mặt khác \(\Delta DBH \backsim \Delta
DAC(g.g)\)
\(\Rightarrow \frac{DB}{DA} =
\frac{DH}{DC} \Rightarrow DB.DC = DA.DH\)
Hay \(DB.DC = DA.AH\ \ (2)\)
Mà \(\Delta AEH \backsim \Delta ADC\ (g.g)\Rightarrow \frac{AE}{AD} = \frac{AH}{AC}\)\(\Rightarrow AE.AC = AD.DH\ (3)\)
Từ \((1),\ (2),\ (3)\) ta có: \(\cos B.cosC = \frac{AE.AC}{AB.AC} =
\frac{AE}{AB}\)
Suy ra \(\cos A = \cos
B.cosC\).
------------------------------------------------------------------
Qua việc luyện tập dạng toán chứng minh biểu thức lượng giác, học sinh không chỉ thành thạo các công thức lượng giác trong tam giác vuông, mà còn nâng cao khả năng suy luận, phân tích và trình bày lời giải chặt chẽ. Đây là kỹ năng quan trọng, góp phần giúp học sinh đạt kết quả cao trong học tập cũng như trong các kỳ thi tuyển sinh vào lớp 10.
Để học tốt chuyên đề này, các em nên thường xuyên làm bài tập từ cơ bản đến nâng cao, đồng thời ghi nhớ và hệ thống hóa các công thức lượng giác. Nhờ đó, việc chứng minh biểu thức lượng giác Toán 9 sẽ trở nên đơn giản, logic và hiệu quả hơn.
