VnDoc.com

Bài toán về điểm cố định trong đường tròn

Chuyên đề Toán lớp 9 luyện thi vào lớp 10

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Chuyên đề luyện thi vào 10: Điểm cố định trong đường tròn

I. Cách giải bài toán về điểm cố định trong đường tròn
II. Bài tập ví dụ cho các bài tập về bài toán điểm cố định trong đường tròn
III. Bài tập tự luyện các bài toán về điểm cố định trong đường tròn

Bài toán về điểm cố định trong đường tròn là một dạng toán nâng cao có trong các đề thi tuyển sinh vào lớp 10 môn Toán. Tài liệu được VnDoc biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 và giúp các bạn học sinh đạt được điểm 9, 10 trong đề thi tuyển sinh vào lớp 10. Mời các bạn tham khảo.

Tài liệu dưới đây được VnDoc biên soạn gồm hướng dẫn giải chi tiết cho dạng bài liên quan đến điểm cố định và tổng hợp các bài toán để các bạn học sinh có thể luyện tập thêm. Qua đó sẽ giúp các bạn học sinh ôn tập các kiến thức, chuẩn bị cho các bài thi học kì và ôn thi vào lớp 10 hiệu quả nhất. Sau đây mời các bạn học sinh cùng tham khảo tải về bản đầy đủ chi tiết.

I. Cách giải bài toán về điểm cố định trong đường tròn

Để giải được bài toán về điểm cố định ta có thể chứng minh theo các cách sau:

+ Chứng minh khoảng cách từ một điểm cố định đến một điểm cố định khác thuộc đường thẳng là không đổi

+ Chứng minh điểm đó là giao điểm của hai đường thẳng cố định

+ Để chứng minh điểm nằm trên đường tròn cố định ta cần chứng minh nó là điểm cuối hay trung điểm của một cung cố định

II. Bài tập ví dụ cho các bài tập về bài toán điểm cố định trong đường tròn

Bài 1: Cho đường tròn (O) luôn thay đổi và ba điểm A, B, C cố định thẳng hàng và sắp xếp theo thứ tự đó. Kẻ AM, AN là hai tiếp tuyến với (O). I là trung điểm của BC. AO cắt MN tại H và (O) tại P và Q (P nằm giữa A và O). BC cắt MN tại K

a, Chứng minh A, M, I, O, N thuộc cùng một đường tròn

b, Chứng minh tích AB.AC = AH.AO và K cố định khi (O) thay đổi

Lời giải:

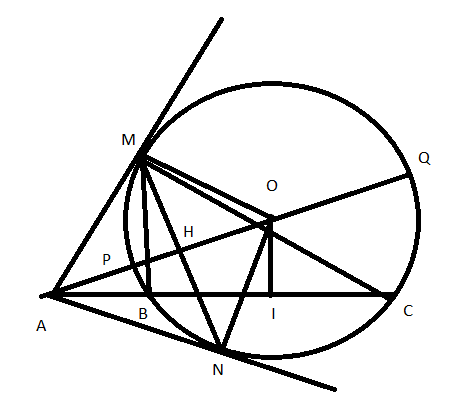
Bài toán về điểm cố định trong đường tròn

a, + Xét tứ giác AMON có $\widehat {AMO} + \widehat {ANO} = {90^0} + {90^0} = {180^0}$

mà hai góc ở vị trí đối nhau

Suy ra tứ giác AMON nội tiếp đường tròn hay 4 điểm A, M, O, N cùng thuộc một đường tròn đường kính AO (1)

+ Trong đường tròn (O) có I là trung điểm của BC $\Rightarrow OI \bot BC \Rightarrow \widehat {OIA} = {90^0}$

Suy ra điểm I thuộc đường tròn đường kính AO (2)

+ Từ (1) và (2) suy ra 5 điểm A, M, O, N, I cùng thuộc một đường tròn

b, Xét tam giác AMB và tam giác ACM có:

$\widehat {MAC}$ chung

$\widehat {AMB} = \widehat {ACM}$ (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung MB)

Suy ra hai tam giác AMB và ACM đồng dạng với nhau theo trường hợp góc - góc

$\Rightarrow \frac{{AM}}{{AC}} = \frac{{AB}}{{AM}}$ (cặp cạnh tương ứng tỉ lệ)

$\Leftrightarrow A{M^2} = AB.AC$ (3)

+ Có OM = ON (= R), AM = AM (tính chất hai tiếp tuyến cắt nhau)

Suy ra AO là đường trung trực của MN

Suy ra AO vuông góc với MN tại H

+ Xét tam giác AMO vuông tại M có đường cao MH:

$\Leftrightarrow A{M^2} = AB.AC$ (hệ thức lượng trong tam giác vuông) (4)

+ Từ (3) và (4) suy ra AB.AC = AH.AO (5)

+ Xét tam giác AHK và tam giác AIO có:

$\widehat {AHK} = \widehat {AIO} = {90^0}$

$\widehat {OAI}$ chung

Suy ra tam giác AHK và tam giác AIO đồng dạng với nhau theo trường hợp góc – góc

$\Rightarrow \frac{{AH}}{{AI}} = \frac{{AK}}{{AO}} \Leftrightarrow AH.AO = AK.AI$ (6)

Từ (5) và (6) suy ra $AK.AI = AB.AC \Leftrightarrow AK = \frac{{AB.AC}}{{AI}}$

Vì A, B, C cố định nên AB, AC, BC không đổi

Mà I là trung điểm của BC nên I cố định hay AI không đổi

Suy ra không đổi. Suy ra AK không đổi hay K cố định (vì A cố định)

Bài 2: Cho nửa đường tròn (O; R), đường kính AB cố định. Trên cùng một nửa mặt phẳng bờ AB chứa đường tròn, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Trên nửa đường tròn, lấy điểm C bất kì. Vẽ tiếp tuyến (O) tại C cắt Ax, By lần lượt tại D và E. AC cắt DO tại M, BC cắt OE tại N

a, Tứ giác CMON là hình gì? Vì sao?

b, Chứng minh tích OM.OD + ON.OE không đổi.

Lời giải:

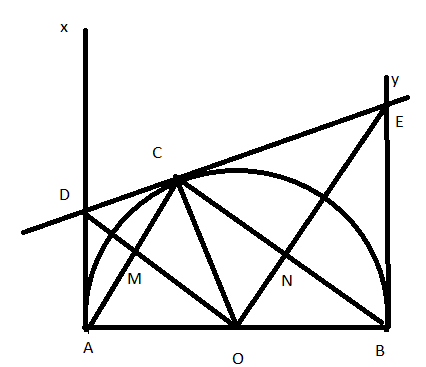
Bài toán về điểm cố định trong đường tròn

a, + Có DA và DC là hai tiếp tuyến cắt nhau tại D. Suy ra DA = DC

lại có OA = OC

suy ra DO là đường trung trực của AC. Suy ra Do vuông góc với AC

mà M là giao điểm của OD và AC. Suy ra $\widehat {OMC} = {90^0}$

+ Tương tự ta cũng có $\widehat {ONC} = {90^0}$

+ Có DC và DA là hai tiếp tuyến cắt nhau tại D suy ra OD là phân giác của $\widehat {AOC}$

EC và EB là hai tiếp tuyến cắt nhau tại E suy ra OE là phân giác của $\widehat {COD}$

Có $\widehat {AOC} + \widehat {COD} = {180^0}$

Suy ra $\widehat {DOC} + \widehat {EOC} = \frac{{{{180}^0}}}{2} = {90^0} \Leftrightarrow \widehat {MON} = {90^0}$

+ Xét tứ giác OMCN có $\widehat {OMC} = \widehat {ONC} = \widehat {MON} = {90^0}$

Suy ra tứ giác OMCN là hình chữ nhật

b, + Xét tam giác AOD vuông tại A có AM vuông góc với DO

Suy ra $A{O^2} = OM.ON \Leftrightarrow OM.ON = {R^2}$ (1)

+ Xét tam giác OBE vuông tại B có BN vuông góc bới OE

Suy ra $O{B^2} = ON.OE \Leftrightarrow ON.OE = {R^2}$ (2)

Từ (1) và (2) suy ra $OM.OD + ON.OE = 2{R^2}$

Do R không đổi nên OM.OD + ON.OE không đổi.

Bài 3: Cho đường tròn (O; R), từ một điểm A trên (O) kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điểm M bất kì ( M khác A) kẻ cát tuyến MNP và gọi K là trung điểm của NP, kẻ tiếp tuyến MB (B là tiếp điểm). Kẻ AC ⊥ MB, BD ⊥ MA, gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB.

1. Chứng minh tứ giác AMBO nội tiếp.

2. Chứng minh năm điểm O, K, A, M, B cùng nằm trên một đường tròn .

3. Chứng minh OI.OM = R²; OI. IM = IA².

4. Chứng minh OAHB là hình thoi.

5. Chứng minh ba điểm O, H, M thẳng hàng.

6. Tìm quỹ tích của điểm H khi M di chuyển trên đường thẳng d

Lời giải:

Hình vẽ minh họa

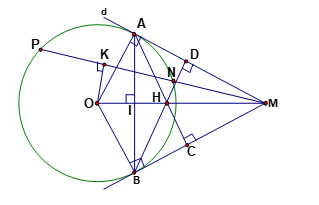
1. (HS tự làm).

2. Vì K là trung điểm NP nên OK ⊥ NP ( quan hệ đường kính và dây cung) $= > \widehat{OKM}\ = \ 90^{0}$ . Theo tính chất tiếp tuyến ta có ∠OAM = 90⁰; ∠OBM = 90⁰. như vậy K, A, B cùng nhìn OM dưới một góc 90⁰ nên cùng nằm trên đường tròn đường kính OM.

Vậy năm điểm O, K, A, M, B cùng nằm trên một đường tròn.

3. Ta có MA = MB (tính chất hai tiếp tuyến cắt nhau); OA = OB = R

=> OM là trung trực của AB => OM ⊥ AB tại I .

Theo tính chất tiếp tuyến ta có $\widehat{OAM}\ = \ 90^{0}$ nên tam giác OAM vuông tại A có AI là đường cao.

Áp dụng hệ thức giữa cạnh và đường cao => OI.OM = OA² hay OI.OM = R²; và OI. IM = IA².

4. Ta có OB ⊥ MB (tính chất tiếp tuyến) ; AC ⊥ MB (gt) => OB // AC hay OB // AH.

OA ⊥ MA (tính chất tiếp tuyến) ; BD ⊥ MA (gt) => OA // BD hay OA // BH.

=> Tứ giác OAHB là hình bình hành; lại có OA = OB (=R) => OAHB là hình thoi.

5. Theo trên OAHB là hình thoi. => OH ⊥ AB; cũng theo trên OM ⊥ AB

=> O, H, M thẳng hàng( Vì qua O chỉ có một đường thẳng vuông góc với AB).

6. (HD) Theo trên OAHB là hình thoi. => AH = AO = R.

Vậy khi M di động trên d thì H cũng di động nhưng luôn cách A cố định một khoảng bằng R. Do đó quỹ tích của điểm H khi M di chuyển trên đường thẳng d là nửa đường tròn tâm A bán kính AH = R

Bài 4 Cho đường tròn (O) bán kính R có hai đường kính AB và CD vuông góc với nhau. Trên đoạn thẳng AB lấy điểm M (M khác O). CM cắt (O) tại N. Đường thẳng vuông góc với AB tại M cắt tiếp tuyến

tại N của đường tròn ở P. Chứng minh :

1. Tứ giác OMNP nội tiếp.

2. Tứ giác CMPO là hình bình hành.

3. Tích CM. CN không phụ thuộc vào vị trí của điểm M.

4. Khi M di chuyển trên đoạn thẳng AB thì P chạy trên đoạn thẳng cố định nào.

Lời giải:

Hình vẽ minh họa

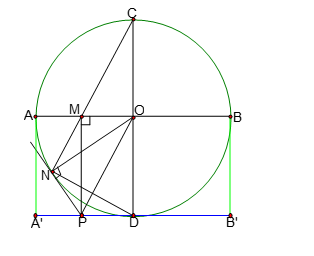
1. Ta có $\widehat{OMP}\ = \ 90^{0}$ (vì $PM\bot AB$ ); $\widehat{ONP\ } = \ 90^{0}$ (vì NP là tiếp tuyến ).

Như vậy M và N cùng nhìn OP dưới một góc bằng 90⁰ => M và N cùng nằm trên đường tròn đường kính OP => Tứ giác OMNP nội tiếp.

2. Tứ giác OMNP nội tiếp => $\widehat{OPM}\ = \widehat{ONM}$ (nội tiếp chắn cung OM)

Tam giác ONC cân tại O vì có ON = OC = R $= > \widehat{ONC\ } = \widehat{OCN}$

$= > \widehat{\ OPM}\ = \widehat{OCM}$ .

Xét hai tam giác OMC và MOP ta có $\left\{ \begin{matrix} \widehat{MOC} = \widehat{OMP} = 90^{0} \\ \widehat{OPM} = \widehat{OCM} \\ \end{matrix} \right.$ $= > \widehat{CMO}\ = \widehat{POM}$ lại có MO là cạnh chung => ∆OMC = ∆MOP => OC = MP. (1)

Theo giả thiết ta có $CD\bot AB;\ PM\bot AB\ = > \ CO//PM\ (2)$

Từ (1) và (2) => Tứ giác CMPO là hình bình hành.

3. Xét hai tam giác OMC và NDC ta có $\widehat{MOC}\ = \ 90^{0}$ ( gt $CD\bot AB$ ); (nội tiếp chắn nửa đường tròn ) $= > \widehat{MOC\ } = \widehat{DNC\ } = \ 90^{0}$ lại có ∠C là góc chung => ∆OMC ∼∆NDC

=> $\frac{CM}{CD}\ = \ \frac{CO}{CN}$ => CM. CN = CO.CD mà CO = R; CD = 2R nên CO.CD = 2R² không đổi => CM.CN =2R² không đổi hay tích CM. CN không phụ thuộc vào vị trí của điểm M.

4. ( HD) Dễ thấy ∆OMC = ∆DPO (c.g.c) => ∠ODP = 90⁰ => P chạy trên đường thẳng cố định vuông góc với CD tại D.

Vì M chỉ chạy trên đoạn thẳng AB nên P chỉ chạy trên đoạn thẳng A’ B’ song song và bằng AB.

Bài 5. Cho hình vuông ABCD, điểm E thuộc cạnh BC. Qua B kẻ đường thẳng vuông góc với DE, đường thẳng này cắt các đường thẳng DE và DC theo thứ tự ở H và K.

1. Chứng minh BHCD là tứ giác nội tiếp .

2. Tính góc CHK.

3. Chứng minh KC. KD = KH.KB

4. Khi E di chuyển trên cạnh BC thì H di chuyển trên đường nào?

Lời giải:

Hình vẽ minh họa

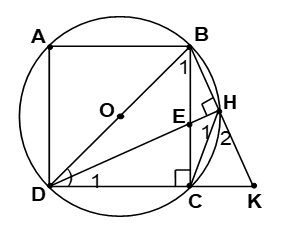
1. Theo giả thiết ABCD là hình vuông nên $\widehat{BCD} = 90^{0};\ BH\bot DE$ tại H nên $\widehat{BHD\ } = \ 90^{0}$ => Như vậy H và C cùng nhìn BD dưới một góc bằng 90⁰ nên H và C cùng nằm trên đường tròn đường kính BD => BHCD là tứ giác nội tiếp.

2. BHCD là tứ giác nội tiếp $= > \widehat{BDC} + \widehat{BHC\ } = 180^{0}$ . (1)

$\widehat{BHK}$ là góc bẹt nên $\widehat{KHC} + \widehat{BHC} = 180^{0}$ (2).

Từ (1) và (2) $= > \widehat{CHK} = \widehat{BDC}$ mà $\widehat{BDC} = \ 45^{0}$ (vì ABCD là hình vuông) => $\widehat{CHK} = 45^{0}$ .

3. Xét ∆KHC và ∆KDB ta có $\widehat{CHK} = \widehat{BDC} = 45^{0};\widehat{K}$ là góc chung

=> ∆KHC ∼ ∆KDB => $\frac{KC}{KB}\ = \ \frac{KH}{KD}$ => KC. KD = KH.KB.

4. (HD) Ta luôn có $\widehat{BHD} = 90^{0}$ và BD cố định nên khi E chuyển động trên cạnh BC cố định thì H chuyển động trên cung BC (E ≡ B thì H ≡ B; E ≡ C thì H ≡ C).

Bài 6: Cho đường tròn (O), đường kính AB = 2R. Một cát tuyến MN quay quanh trung điểm H của OB.

1. Chứng minh khi MN di động , trung điểm I của MN luôn nằm trên một đường tròn cố định.

2. Từ A kẻ Ax ⊥ MN, tia BI cắt Ax tại C. Chứng minh tứ giác CMBN là hình bình hành.

3. Chứng minh C là trực tâm của tam giác AMN.

4. Khi MN quay quanh H thì C di động trên đường nào.

5. Cho AM. AN = 3R² , AN = R $\sqrt{3}$ . Tính diện tích phần hình tròn (O) nằm ngoài tam giác AMN.

Lời giải:

Hình vẽ minh họa

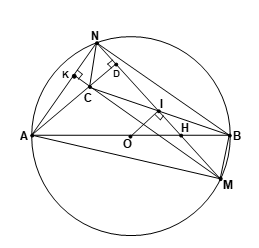
1. I là trung điểm của MN => OI ⊥ MN tại I (quan hệ đường kính và dây cung)

=> ∠OIH = 90⁰

OH cố định nên khi MN di động thì I cũng di động nhưng luôn nhìn OH cố định dưới một góc 90⁰ do đó I di động trên đường tròn đường kính OH.

Vậy khi MN di động, trung điểm I của MN luôn nằm trên một đường tròn cố định.

2. Theo giả thiết Ax ⊥ MN; theo trên OI ⊥ MN tại I

=> OI // Ax hay OI // AC mà O là trung điểm của AB

=> I là trung điểm của BC, lại có I là trung điểm của MN (giả thiết)

=> CMBN là hình bình hành (Vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).

3. CMBN là hình bình hành

=> MC // BN mà BN ⊥ AN (vì ∠ANB = 90⁰ do là góc nội tiếp chắn nửa đường tròn)

=> MC ⊥ AN; theo trên AC ⊥ MN

=> C là trực tâm của tam giác AMN.

4. Ta có H là trung điểm của OB; I là trung điểm của BC

=> IH là đường tung bình của ∆OBC

=> IH // OC

Theo giả thiết Ax ⊥ MN hay IH ⊥ Ax

=> OC ⊥ Ax tại C => ∠OCA = 90⁰

=> C thuộc đường tròn đường kính OA cố định.

Vậy khi MN quay quanh H thì C di động trên đường tròn đường kính OA cố định.

5. Ta có AM. AN = 3R² , AN = R $\sqrt{3}$ . => AM =AN = R $\sqrt{3}$

=> ∆AMN cân tại A. (1)

Xét ∆ABN vuông tại N ta có:

AB = 2R; AN = R $\sqrt{3}$ => BN = R => ∠ABN = 60⁰ .

∠ABN = ∠AMN (nội tiếp cùng chắn cung AN)

=> ∠AMN = 60⁰ (2).

Từ (1) và (2) => ∆AMN là tam giác đều => S_∆AMN = $\frac{3R^{2}\sqrt{3}}{4}$ .

=> S = S_(O) - S_∆AMN = $\pi R^{2}$ - $\frac{3R^{2}\sqrt{3}}{4}$ = $\frac{R^{2}\left( 4\pi - 3\sqrt{3} \right)}{4}$

Bài 7. Cho điểm C cố định trên một đường thẳng xy. Dựng nửa đường thẳng Cz vuông góc với xy và lấy trên đó 2 điểm cố định A, B (A ở giữa C và B). M là một điểm di động trên xy. Đường vuông góc với AM tại A và với BM tại B cắt nhau tại P.

a. Chứng minh tứ giác MABP nội tiếp được và tâm O của đường tròn này nằm trên một đường thẳng cố định đi qua điểm giữa L của AB.

b. Kẻ PI $\bot$ Cz. Chứng minh I là một điểm cố định.

c. BM và AP cắt nhau ở H; BP và AM cắt nhau ở K. Chứng minh rằng KH $\bot$ PM.

d. Cho N là trung điểm của KH. Chứng minh các điểm N; L; O thẳng hàng.

Lời giải

a) MABP nội tiếp đường tròn đường kính MP.(quĩ tích cung chứa góc 90⁰…)

OA = OB = R_(O)

$\Rightarrow$ O thuộc đường trung trực AB đi qua L

là trung điểm AB…

b) IP // CM ( $\bot$ Cz) $\Rightarrow$ MPIC là hình thang. $\Rightarrow$ IL = LC không đổi

vì A, B, C cố định. $\Rightarrow$ I cố định.

c) PA $\bot$ KM ; PK $\bot$ MB $\Rightarrow$ H là trực tâm ∆ PKM

$\Rightarrow$ KH $\bot$ PM

d) AHBK nội tiếp đường tròn đường kính KH (quỹ tích cung chứa góc…)

$\Rightarrow$ N là tâm đường tròn ngoại tiếp … $\Rightarrow$ NE = NA = R_(N)

$\Rightarrow$ N thuộc đường trung trực AB

$\Rightarrow$ O, L, N thẳng hàng.

III. Bài tập tự luyện các bài toán về điểm cố định trong đường tròn

Bài tập 1. Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho AI = 2/3 AO. Kẻ dây MN vuông góc với AB tại I, gọi C là điểm tuỳ ý thuộc cung lớn MN sao cho C không trùng với M, N và B. Nối AC cắt MN tại E.

a. Chứng minh tứ giác IECB nội tiếp .

b. Chứng minh tam giác AME đồng dạng với tam giác ACM.

c. Chứng minh AM² = AE.AC.

d. Chứng minh AE. AC - AI.IB = AI² .

e. Hãy xác định vị trí của C sao cho khoảng cách từ N đến tâm đường tròn ngoại tiếp tam giác CME là nhỏ nhất.

Bài tập 2. Cho đường tròn (O; R) và một đường thẳng (d) cố định không cắt (O; R). Hạ OH $\bot$ (d) (H $\in$ d). M là một điểm thay đổi trên (d) (M $\neq$ H). Từ M kẻ 2 tiếp tuyến MP và MQ (P, Q là tiếp điểm) với (O; R). Dây cung PQ cắt OH ở I; cắt OM ở K.

a. Chứng minh 5 điểm O, Q, H, M, P cùng nằm trên 1 đường tròn.

b. Chứng minh IH.IO = IQ.IP

c. Giả sử $\widehat{PMQ}$ = 60⁰. Tính tỉ số diện tích 2 tam giác: ∆MPQ và ∆OPQ.

Bài tập 3. Cho điểm C cố định trên một đường thẳng xy. Dựng nửa đường thẳng Cz vuông góc với xy và lấy trên đó 2 điểm cố định A, B (A ở giữa C và B). M là một điểm di động trên xy. Đường vuông góc với AM tại A và với BM tại B cắt nhau tại P.

a. Chứng minh tứ giác MABP nội tiếp được và tâm O của đường tròn này nằm trên một đường thẳng cố định đi qua điểm giữa L của AB.

b. Kẻ PI $\bot$ Cz. Chứng minh I là một điểm cố định.

c. BM và AP cắt nhau ở H; BP và AM cắt nhau ở K. Chứng minh rằng KH $\bot$ PM.

d. Cho N là trung điểm của KH. Chứng minh các điểm N; L; O thẳng hàng.

Bài tập 4. Cho đường tròn tâm O, bán kính R, có hai đường kính AB, CD vuông góc với nhau. M là một điểm tuỳ ý thuộc cung nhỏ AC. Nối MB, cắt CD ở N.

a. Chứng minh: tia MD là phân giác của góc AMB.

b. Chứng minh:∆BOM ~ ∆BNA. Chứng minh: BM.BN không đổi.

c. Chứng minh: tứ giác ONMA nội tiếp. Gọi I là tâm đường tròn ngoại tiếp tứ giác ONMA, I di động như thế nào?

Bài tập 5. Cho đường tròn (O; R) có 2 đường kính cố định AB $\bot$ CD.

a) Chứng minh: ACBD là hình vuông.

b). Lấy điểm E di chuyển trên cung nhỏ BC (E $\neq$ B; E $\neq$ C). Trên tia đối của tia EA lấy đoạn EM = EB. Chứng tỏ: ED là tia phân giác của $\widehat{AEB}$ và ED // MB.

c). Suy ra CE là đường trung trực của BM và M di chuyển trên đường tròn mà ta phải xác định tâm và bán kính theo R.

Bài tập 6. Cho ∆ ABC đều, nội tiếp trong đường tròn (O; R). Gọi AI là một đường kính cố định và D là điểm di động trên cung nhỏ AC (D $\neq$ A và D $\neq$ C).

a. Tính cạnh của ∆ABC theo R và chứng tỏ AI là tia phân giác của $\widehat{BAC}$ .

b. Trên tia DB lấy đoạn DE = DC. Chứng tỏ ∆CDE đều và DI $\bot$ CE.

c. Suy ra E di động trên đường tròn mà ta phải xác định tâm và giới hạn.

d. Tính theo R diện tích ∆ADI lúc D là điểm chính giữa cung nhỏ AC.

Đáp án chi tiết bài tập tự rèn luyện

Bài tập 1

Hình vẽ minh họa:

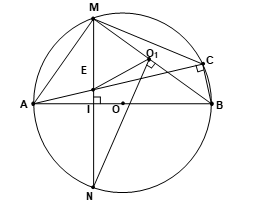
a. Theo giả thiết MN ⊥AB tại I => ∠EIB = 90⁰; ∠ ACB nội tiếp chắn nửa đường tròn nên ∠ACB = 90⁰ hay ∠ECB = 90⁰

=> ∠EIB + ∠ECB = 180⁰ mà đây là hai góc đối của tứ giác IECB nên tứ giác IECB là tứ giác nội tiếp.

b. Theo giả thiết MN ⊥AB => A là trung điểm của cung MN => ∠AMN = ∠ACM ( hai góc nội tiếp chắn hai cung bằng nhau) hay ∠AME = ∠ACM. Lại thấy ∠CAM là góc chung của hai tam giác AME và AMC do đó tam giác AME đồng dạng với tam giác ACM.

c. Theo trên ∆AME ∼ ∆ ACM => $\frac{AM}{AC}\ = \ \frac{AE}{AM}$ => AM² = AE.AC

d. ∠AMB = 90⁰ (nội tiếp chắn nửa đường tròn ); MN ⊥AB tại I => ∆AMB vuông tại M có MI là đường cao => MI² = AI.BI ( hệ thức giữa cạnh và đường cao trong tam giác vuông) .

Áp dụng định lí Ptthagore trong tam giác AIM vuông tại I ta có AI² = AM² – MI² => AI² = AE.AC - AI.BI .

e. Theo trên ∠AMN = ∠ACM => AM là tiếp tuyến của đường tròn ngoại tiếp ∆ ECM; Nối MB ta có ∠AMB = 90⁰ , do đó tâm O₁ của đường tròn ngoại tiếp ∆ ECM phải nằm trên BM. Ta thấy NO₁ nhỏ nhất khi NO₁ là khoảng cách từ N đến BM => NO₁ ⊥BM.

Gọi O₁ là chân đường vuông góc kẻ từ N đến BM ta được O₁ là tâm đường tròn ngoại tiếp ∆ ECM có bán kính là O₁M. Do đó để khoảng cách từ N đến tâm đường tròn ngoại tiếp tam giác CME là nhỏ nhất thì C phải là giao điểm của đường tròn tâm O₁ bán kính O₁M với đường tròn (O) trong đó O₁ là hình chiếu vuông góc của N trên BM.

✨ Bài viết chỉ trích dẫn một phần nội dung, mời bạn tải tài liệu đầy đủ để nắm trọn kiến thức.

----------------------------------------------------

Ngoài các dạng Toán 9 ôn thi vào lớp 10 trên, mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt!

Tải về

Chọn file muốn tải về: