Chứng minh các tam giác đặc biệt trong đường tròn
Chuyên đề luyện thi vào 10: Chứng minh các tam giác đặc biệt trong đường tròn
Chứng minh các tam giác đặc biệt trong đường tròn là một dạng toán thường gặp trong đề thi tuyển sinh vào lớp 10 môn Toán được VnDoc biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hơn. Mời các bạn tham khảo.
- Ôn thi vào lớp 10 chuyên đề 10: Chứng minh các hệ thức hình học
- Các dạng Toán thi vào 10
- Các bài toán Hình học ôn thi vào lớp 10
I. Cách chứng minh các tam giác đặc biệt
1. Tam giác cân
+ Tam giác có hai cạnh bằng nhau là tam giác cân
+ Tam giác có hai góc bằng nhau là tam giác cân
+ Tam giác có đường cao đồng thời là đường phân giác hay đường trung tuyến thì tam giác ấy là tam giác cân
Cách dựng tam giác ABC cân tại A
– Vẽ cạnh BC
– Vẽ cung tròn tâm B, bán kính r
– Vẽ cung tròn tâm C, bán kính r
Hai cung tròn cắt nhau tại A.
Tam giác ABC là tam giác cần vẽ.
2. Tam giác đều
+ Tam giác có ba cạnh bằng nhau là tam giác đều
+ Tam giác có ba góc bằng nhau là tam giác đều
+ Tam giác cân có một góc bằng 600 là tam giác đều
+ Tam giác cân tại hai đỉnh thì tam giác ấy là tam giác đều
Cách dựng tam giác đều ABC
– Vẽ cạnh BC
– Vẽ (B; BC) và (C; BC)
– (B; BC) ∩ (C; BC) tại A
ABC là tam giác đều cần vẽ.
3. Tam giác vuông
+ Tam giác có một góc vuông thì tam giác ấy là tam giác vuông
+ Tam giác có hai cạnh nằm trên hai đường thẳng vuông góc thì tam giác ấy là tam giác vuông
+ Sử dụng định lý Pitago đảo để chứng minh tam giác là tam giác vuông
+ Tam giác nội tiếp đường tròn và có một cạnh là đường kính thì tam giác ấy là tam giác vuông
Cách dựng tam giác ABC vuông tại A
Cho trước cạnh huyền BC = 4,5 cm và cạnh góc vuông AC = 2 cm.
– Dựng đoạn AC = 2 cm
– Dựng góc CAx bằng 90o.
– Dựng cung tròn tâm C bán kinh 4,5 cm cắt Ax tại B. Nối BC ta có Δ ABC cần dựng.
4. Tam giác vuông cân
+ Tam giác vuông có hai cạnh góc vuông bằng nhau thì tam giác ấy là tam giác vuông cân
+ Tam giác vuông có một góc bằng 450 thì tam giác ấy là tam giác vuông cân
+ Tam giác cân có một góc đáy bằng 450 thì tam giác ấy là tam giác vuông cân
II. Bài tập ví dụ cho bài toán chứng minh các tam giác đặc biệt trong đường tròn
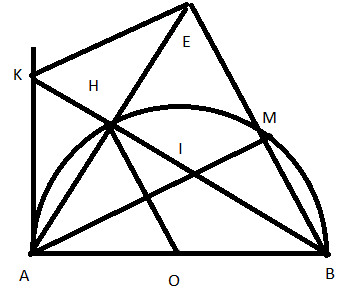
Bài 1: Cho nửa đường tròn (O; R) đường kính AB. Điểm M thuộc nửa đường tròn. Gọi H là điểm chính giữa cung AM. Tia BH cắt AM tại I. Tiếp tuyến của nửa đường tròn tại A cắt BH tại K. Nối AH cắt BM tại E. Chứng minh:
a, Tam giác BAE là tam giác cân
b, KH.KB = KE.KE
Lời giải:
a, + Có ![]() \(\widehat {AHB}\) nhìn đường kính AB nên
\(\widehat {AHB}\) nhìn đường kính AB nên ![]() \(\widehat {AHB} = {90^0}\)
\(\widehat {AHB} = {90^0}\)
Suy ra BH vuông góc với AH hay BH vuông góc với AE
+ Tam giác BAE có BH vuông góc với AE nên BH là đường cao của tam giác ABE (1)
+ Có ![]() \(\widehat {ABH}\) là góc nội tiếp chắn cung AH
\(\widehat {ABH}\) là góc nội tiếp chắn cung AH
![]() \(\widehat {MBH}\)là góc nội tiếp chắn cung HM
\(\widehat {MBH}\)là góc nội tiếp chắn cung HM
Mà số đo cung AH bằng số đo cung HM
Suy ra ![]() \(\widehat {ABH} = \widehat {HBM}\) hay BH là phân giác của
\(\widehat {ABH} = \widehat {HBM}\) hay BH là phân giác của ![]() \(\widehat {ABE}\)(1)
\(\widehat {ABE}\)(1)
+ Từ (1) và (2) có BH vừa là đường cao vừa là đường phân giác của tam giác ABE nên tam giác ABE cân tại B (tính chất)
b, + Có tam giác ABE là tam giác cân tại B, BH là đường cao nên BH là đường trung tuyến nên AH = HE
+ Xét tam giác AKE có KH vuông góc với AE và AH = HE nên tam giác AKE cân tại K. Suy ra AK = KE (tính chất)
+ Xét tam giác AKB có ![]() \(\widehat {BAK} = {90^0}\) và AH vuông góc với BK nên
\(\widehat {BAK} = {90^0}\) và AH vuông góc với BK nên ![]() \(A{K^2} = KH.KB\)
\(A{K^2} = KH.KB\)
mà AK = KE (chứng minh trên) nên ![]() \(K{E^2} = KH.KB\)(đpcm)
\(K{E^2} = KH.KB\)(đpcm)
Bài 2: Cho nửa đường tròn (O) đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O). Tiếp tuyến thứ ba tiếp xúc với nửa đường tròn (O) tại M cắt Ax, By lần lượt tại D và E. Chứng minh tam giác DOE là tam giác vuông
Lời giải:
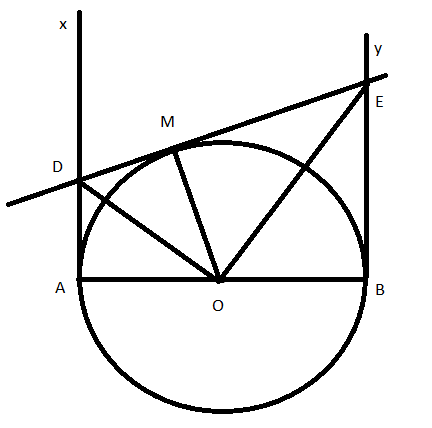
+ Có Ax và MD là hai tiếp tuyến cắt nhau tại D suy ra OD là tia phân giác của ![]() \(\widehat {AOM}\)
\(\widehat {AOM}\)
+ Có By và ME là hai tiếp tuyến cắt nhau tại E suy ra OE là tia phân giác của ![]() \(\widehat {BOM}\)
\(\widehat {BOM}\)
+ Có ![]() \(\widehat {AOM}\)và
\(\widehat {AOM}\)và ![]() \(\widehat {BOM}\) là hai góc kề bù suy ra
\(\widehat {BOM}\) là hai góc kề bù suy ra ![]() \(\widehat {BOM} + \widehat {AOM} = {90^0}\)
\(\widehat {BOM} + \widehat {AOM} = {90^0}\)
Mà ![]() \(\widehat {AOD} = \widehat {DOM} = \frac{{\widehat {AOM}}}{2}\)(OD là tia phân giác của
\(\widehat {AOD} = \widehat {DOM} = \frac{{\widehat {AOM}}}{2}\)(OD là tia phân giác của ![]() \(\widehat {AOM}\))
\(\widehat {AOM}\))
Và ![]() \(\widehat {BOE} = \widehat {MOE} = \frac{{\widehat {BOM}}}{2}\)(OE là tia phân giác của
\(\widehat {BOE} = \widehat {MOE} = \frac{{\widehat {BOM}}}{2}\)(OE là tia phân giác của ![]() \(\widehat {BOM}\))
\(\widehat {BOM}\))
Suy ra ta có
 \(\begin{array}{l}
2\widehat {DOM} + 2\widehat {MOE} = {180^0}\\
\Leftrightarrow \widehat {DOM} + \widehat {MOE} = {90^0}\\
\Leftrightarrow \widehat {DOE} = {90^0}
\end{array}\)
\(\begin{array}{l}
2\widehat {DOM} + 2\widehat {MOE} = {180^0}\\
\Leftrightarrow \widehat {DOM} + \widehat {MOE} = {90^0}\\
\Leftrightarrow \widehat {DOE} = {90^0}
\end{array}\)
Vậy tam giác DOE là tam giác vuông.
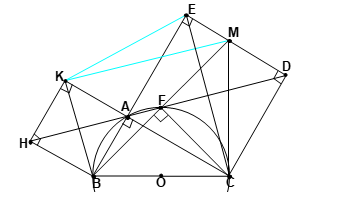
Bài 3. Cho tam giác ABC vuông ở A. Dựng ở miền ngoài tam giác ABC các hình vuông ABHK, ACD.
1. Chứng minh ba điểm H, A, D thẳng hàng.
2. Đường thẳng HD cắt đường tròn ngoại tiếp tam giác ABC tại F, chứng minh FBC là tam giác vuông cân.
3. Cho biết ∠ABC > 450 ; gọi M là giao điểm của BF và ED, Chứng minh 5 điểm B, K, E, M, C cùng nằm trên một đường tròn.
4. Chứng minh MC là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
Hướng dẫn giải
Hình vẽ minh họa
1. Theo giả thiết ABHK là hình vuông => ∠BAH = 450
Tứ giác AEDC là hình vuông ![]() \(BAC\)=> ∠CAD = 450; tam giác ABC vuông ở A
\(BAC\)=> ∠CAD = 450; tam giác ABC vuông ở A
![]() \(\Rightarrow \widehat{BAC} =
90^{0}\)
\(\Rightarrow \widehat{BAC} =
90^{0}\)
![]() \(\Rightarrow \widehat{BAH} +
\widehat{BAC} + \widehat{CAD} = 45^{0} + 90^{0} + 45^{0} =
180^{0}\)
\(\Rightarrow \widehat{BAH} +
\widehat{BAC} + \widehat{CAD} = 45^{0} + 90^{0} + 45^{0} =
180^{0}\)
=> Ba điểm H, A, D thẳng hàng.
2. Ta có ![]() \(\widehat{BFC} = 90^{0}\) (nội tiếp chắn nửa đường tròn) nên tam giác BFC vuông tại F. (1).
\(\widehat{BFC} = 90^{0}\) (nội tiếp chắn nửa đường tròn) nên tam giác BFC vuông tại F. (1).
![]() \(\widehat{FBC} = \widehat{FAC}\) (nội tiếp cùng chắn cung FC) mà theo trên
\(\widehat{FBC} = \widehat{FAC}\) (nội tiếp cùng chắn cung FC) mà theo trên ![]() \(\widehat{CAD} = 45^{0}\) hay
\(\widehat{CAD} = 45^{0}\) hay ![]() \(\widehat{FAC} = 45^{0}\) (2).
\(\widehat{FAC} = 45^{0}\) (2).
Từ (1) và (2) suy ra ∆FBC là tam giác vuông cân tại F.
3. Theo trên![]() \(\widehat{BFC} = 90^{0}
\Rightarrow \widehat{CFM} = 90^{0}\)(vì là hai góc kề bù);
\(\widehat{BFC} = 90^{0}
\Rightarrow \widehat{CFM} = 90^{0}\)(vì là hai góc kề bù); ![]() \(\widehat{CDM} = 90^{0}\) (tính chất hình vuông).
\(\widehat{CDM} = 90^{0}\) (tính chất hình vuông).
![]() \(\Rightarrow \widehat{CFM} + \widehat{CDM}
= 180^{0}\) mà đây là hai góc đối nên tứ giác CDMF nội tiếp một đường tròn suy ra
\(\Rightarrow \widehat{CFM} + \widehat{CDM}
= 180^{0}\) mà đây là hai góc đối nên tứ giác CDMF nội tiếp một đường tròn suy ra ![]() \(\widehat{CDF} =
\widehat{CMF}\), mà
\(\widehat{CDF} =
\widehat{CMF}\), mà ![]() \(\widehat{CDF} =
45^{0}\) (vì AEDC là hình vuông)
\(\widehat{CDF} =
45^{0}\) (vì AEDC là hình vuông)
![]() \(\ \Rightarrow \widehat{CMF} = \ 45^{0}
\Rightarrow \widehat{CMB} = 45^{0}\).
\(\ \Rightarrow \widehat{CMF} = \ 45^{0}
\Rightarrow \widehat{CMB} = 45^{0}\).
Ta cũng có ![]() \(\widehat{CEB} =
45^{0}\) (vì AEDC là hình vuông);
\(\widehat{CEB} =
45^{0}\) (vì AEDC là hình vuông); ![]() \(\widehat{BKC} = 45^{0}\) (vì ABHK là hình vuông).
\(\widehat{BKC} = 45^{0}\) (vì ABHK là hình vuông).
Như vậy K, E, M cùng nhìn BC dưới một góc bằng 450 nên cùng nằm trên cung chứa góc 450 dựng trên BC
=> 5 điểm B, K, E, M, C cùng nằm trên một đường tròn.
4. ∆CBM có ![]() \(\widehat{B} = \
45^{0};\widehat{M} = 45^{0} \rightarrow \widehat{BCM} = 45^{0}\) hay MC ⊥ BC tại C
\(\widehat{B} = \
45^{0};\widehat{M} = 45^{0} \rightarrow \widehat{BCM} = 45^{0}\) hay MC ⊥ BC tại C
=> MC là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
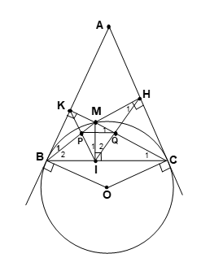
Bài 4: Cho đường tròn (O), BC là dây bất kì (BC< 2R). Kẻ các tiếp tuyến với đường tròn (O) tại B và C chúng cắt nhau tại A. Trên cung nhỏ BC lấy một điểm M rồi kẻ các đường vuông góc MI, MH, MK xuống các cạnh tương ứng BC, AC, AB. Gọi giao điểm của BM, IK là P; giao điểm của CM, IH là Q.
1. Chứng minh tam giác ABC cân.
2. Các tứ giác BIMK, CIMH nội tiếp .
3. Chứng minh MI2 = MH.MK.
Hướng dẫn giải
Hình vẽ minh họa
1. Theo tính chất hai tiếp tuyến cắt nhau ta có AB = AC => ∆ABC cân tại A.
2. Theo giả thiết  \(\left\{ \begin{matrix}
MI\bot BC\ \Rightarrow \widehat{MIB} = 90^{0} \\
MK\bot AB \Rightarrow \widehat{MKB} = 90^{0} \\
\end{matrix} \right.\).
\(\left\{ \begin{matrix}
MI\bot BC\ \Rightarrow \widehat{MIB} = 90^{0} \\
MK\bot AB \Rightarrow \widehat{MKB} = 90^{0} \\
\end{matrix} \right.\).
![]() \(\Rightarrow \widehat{MIB}\ +
\widehat{MKB} = 180^{0}\) mà đây là hai góc đối => Tứ giác BIMK nội tiếp
\(\Rightarrow \widehat{MIB}\ +
\widehat{MKB} = 180^{0}\) mà đây là hai góc đối => Tứ giác BIMK nội tiếp
* ( Chứng minh tứ giác CIMH nội tiếp tương tự tứ giác BIMK )
3. Theo trên tứ giác BIMK nội tiếp ![]() \(\Rightarrow \widehat{KMI} + \widehat{KBI} =
180^{0}\); tứ giác CHMI nội tiếp
\(\Rightarrow \widehat{KMI} + \widehat{KBI} =
180^{0}\); tứ giác CHMI nội tiếp
![]() \(\Rightarrow \widehat{HMI} +
\widehat{HCI} = 180^{0}\)
\(\Rightarrow \widehat{HMI} +
\widehat{HCI} = 180^{0}\)
Mà ![]() \(\widehat{KBI} = \widehat{HCI}\) (vì tam giác ABC cân tại A)
\(\widehat{KBI} = \widehat{HCI}\) (vì tam giác ABC cân tại A)
![]() \(\Rightarrow \widehat{KMI} =
\widehat{HMI}\ (1)\)
\(\Rightarrow \widehat{KMI} =
\widehat{HMI}\ (1)\)
Theo trên tứ giác BIMK nội tiếp
![]() \(\Rightarrow \widehat{B_{1}} =
\widehat{I_{1}}\) ( nội tiếp cùng chắn cung KM); tứ giác CHMI nội tiếp
\(\Rightarrow \widehat{B_{1}} =
\widehat{I_{1}}\) ( nội tiếp cùng chắn cung KM); tứ giác CHMI nội tiếp
![]() \(\Rightarrow \widehat{H_{1}} =
\widehat{C_{1}}\) ( nội tiếp cùng chắn cung IM).
\(\Rightarrow \widehat{H_{1}} =
\widehat{C_{1}}\) ( nội tiếp cùng chắn cung IM).
Mà ![]() \(\widehat{B_{1}} =
\widehat{C_{1}}\left( = \frac{1}{2}\ sd\widehat{BM} \right) \Rightarrow
\widehat{I_{1}} = \widehat{H_{1}}(2)\)
\(\widehat{B_{1}} =
\widehat{C_{1}}\left( = \frac{1}{2}\ sd\widehat{BM} \right) \Rightarrow
\widehat{I_{1}} = \widehat{H_{1}}(2)\)
Từ (1) và (2) => ∆MKI đồng dạng ∆MIH => ![]() \(\frac{MI}{MH}\ = \ \frac{MK}{MI}\) => MI2 = MH.MK.
\(\frac{MI}{MH}\ = \ \frac{MK}{MI}\) => MI2 = MH.MK.
Bài 5: Cho nửa đường tròn (O) đường kính AB và K là điểm chính giữa của cung AB. Trên cung AB lấy một điểm M (khác K; B). Trên tia AM lấy điểm N sao cho AN = BM. Kẻ dây BP song song với KM. Gọi Q là giao điểm của các đường thẳng AP, BM.
a. So sánh hai tam giác: ∆AKN và ∆BKM.
b. Chứng minh: ∆KMN vuông cân.
c. Tứ giác ANKP là hình gì? Vì sao?
Hướng dẫn giải
Hình vẽ minh họa
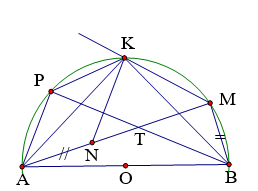
a) ∆ AKN = ∆ BKM(c.g.c)
b) HS tự chứng minh. ∆ KMN vuông cân.
c) ∆ KMN vuông ![]() \(\Rightarrow\) KN
\(\Rightarrow\) KN![]() \(\bot\)KM mà KM // BP
\(\bot\)KM mà KM // BP ![]() \(\Rightarrow\)KN
\(\Rightarrow\)KN ![]() \(\bot\)BP
\(\bot\)BP
![]() \(\widehat{APB}\) = 900 (góc nội tiếp…)
\(\widehat{APB}\) = 900 (góc nội tiếp…) ![]() \(\Rightarrow\)AP
\(\Rightarrow\)AP ![]() \(\bot\) BP
\(\bot\) BP
![]() \(\Rightarrow\) KN // AP (
\(\Rightarrow\) KN // AP (![]() \(\bot\)BP)
\(\bot\)BP)
KM // BP ![]() \(\Rightarrow\)
\(\Rightarrow\) ![]() \(\widehat{KMN} = \widehat{PAT} =
45^{0}\)
\(\widehat{KMN} = \widehat{PAT} =
45^{0}\)
Mà ![]() \(\widehat{PAM} = \widehat{PKU} =
\frac{\widehat{PKM}}{2} = 45^{0}\)
\(\widehat{PAM} = \widehat{PKU} =
\frac{\widehat{PKM}}{2} = 45^{0}\)
![]() \(\widehat{PKN} = 45^{0}\);
\(\widehat{PKN} = 45^{0}\); ![]() \(\widehat{KNM} = 45^{0} \Rightarrow\) PK // AN .
\(\widehat{KNM} = 45^{0} \Rightarrow\) PK // AN .
Vậy ANPK là hình bình hành.
Bài 6: Cho ∆ABC có ![]() \(\widehat{A}\)=
\(\widehat{A}\)=![]() \(60^{0}\) nội tiếp trong đường tròn (O), đường cao AH cắt đường tròn ở D, đường cao BK cắt AH ở E.
\(60^{0}\) nội tiếp trong đường tròn (O), đường cao AH cắt đường tròn ở D, đường cao BK cắt AH ở E.
a. Chứng minh: ![]() \(\widehat{BKH} =
\widehat{BCD}\).
\(\widehat{BKH} =
\widehat{BCD}\).
b. Tính ![]() \(\widehat{BEC}\).
\(\widehat{BEC}\).
c. Biết cạnh BC cố định, điểm A chuyển động trên cung lớn BC. Hỏi tâm I của đườngtròn nội tiếp ∆ABC chuyển động trên đường nào? Nêu cách dựng đường đó (chỉ nêu cách dựng) và cách xác định rõ nó (giới hạn đường đó).
d. Chứng minh: ∆IOE cân ở I.
Hướng dẫn giải
Hình vẽ minh họa
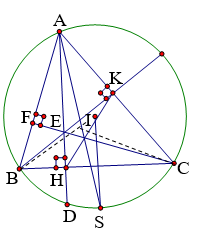
a) ABHK nội tiếp ![]() \(\Rightarrow
\widehat{BKH} = \widehat{BAH}\);
\(\Rightarrow
\widehat{BKH} = \widehat{BAH}\);
![]() \(\widehat{BCD} = \widehat{BAH}\) ( cùng chắn cung BD)
\(\widehat{BCD} = \widehat{BAH}\) ( cùng chắn cung BD) ![]() \(\Rightarrow \widehat{BCD}
= \widehat{BKH}\)
\(\Rightarrow \widehat{BCD}
= \widehat{BKH}\)
b) CE cắt AB ở F.
AFEK nội tiếp![]() \(\Rightarrow \widehat{FEK} =
180^{0} - \widehat{\ A\ } = 180^{0} - 60^{0} = 120^{0}
\Rightarrow\)
\(\Rightarrow \widehat{FEK} =
180^{0} - \widehat{\ A\ } = 180^{0} - 60^{0} = 120^{0}
\Rightarrow\) ![]() \(\widehat{BEC}\) = 1200
\(\widehat{BEC}\) = 1200
c) ![]() \(\widehat{BIC} = 180^{0} -
\frac{\widehat{\ B\ } + \widehat{\ C\ }}{2} = 180^{0} -
\frac{120^{0}}{2} = 120^{0}\)
\(\widehat{BIC} = 180^{0} -
\frac{\widehat{\ B\ } + \widehat{\ C\ }}{2} = 180^{0} -
\frac{120^{0}}{2} = 120^{0}\)
Vậy I chuyển động trên cung chứa góc 1200 dựng trên đoạn BC, cung
này nằm trong đường tròn tâm (O).
d) Trong đường tròn (O) có ![]() \(\widehat{DAS}\) = sđ
\(\widehat{DAS}\) = sđ ![]() \(\frac{\widehat{DS}}{2}\); trong đường tròn (S) có
\(\frac{\widehat{DS}}{2}\); trong đường tròn (S) có ![]() \(\widehat{ISO}\) = sđ
\(\widehat{ISO}\) = sđ ![]() \(\frac{\widehat{IO}}{2}\)
\(\frac{\widehat{IO}}{2}\)
Vì ![]() \(\widehat{DAS}\) =
\(\widehat{DAS}\) = ![]() \(\widehat{ISO}\) (so le trong) nên:
\(\widehat{ISO}\) (so le trong) nên: ![]() \(\frac{\widehat{DS}}{2}\)=
\(\frac{\widehat{DS}}{2}\)=![]() \(\frac{\widehat{IO}}{2}\) mà
\(\frac{\widehat{IO}}{2}\) mà ![]() \(\widehat{DS}\) =
\(\widehat{DS}\) = ![]() \(\widehat{IE} \Rightarrow \widehat{IO}\) =
\(\widehat{IE} \Rightarrow \widehat{IO}\) = ![]() \(\widehat{IE} \Rightarrow\) điều phải chứng minh
\(\widehat{IE} \Rightarrow\) điều phải chứng minh
III. Bài tập tự luyện về bài toán chứng minh các tam giác đặc biệt trong đường tròn
Bài 1: Cho đường tròn (O; R) đường kính AB. M là trung điểm của OA. Kẻ dây CD vuông góc với OA tại M. Chứng minh:
a, Chứng minh tứ giác ACOD là hình thoi.
b, Chứng minh BCD đều.
c, Tính diện tích tam giác BCD theo R.
Bài 2: Cho đường tròn (O; R), M là một điểm ở ngoài đường tròn sao cho OM = 2R. Tia MO cắt đường tròn ở A và B (A nằm giữa M và O). Từ M kẻ 2 tiếp tuyến MC và MD với đường tròn (O), H là giao điểm của MO với CD. Chứng minh:
a, Tứ giác MCOD nội tiếp, MO vuông góc với CD.
b, Tam giác MCD là tam giác đều.
Bài 3: Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn sao cho OA = 2R. Vẽ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Chứng minh tam giác ABC đều.
Bài 4: Từ một điểm ở ngoài đường tròn (O), kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Gọi I là trung điểm của đoạn AB, kẻ tiếp tuyến IM với đường tròn (O) (M là tiếp điểm). Chứng minh tam giác ABM là tam giác vuông.
Bài 5: Cho đường tròn tâm O. Gọi I là trung điểm của bán kính OA. Qua I kẻ dây BC vuông góc với OA. Chứng minh tứ giác ABOC là hình thoi.
Bài 6: Cho đường tròn tâm O bán kính R, đường kính AB. M là trung điểm của AO. Kẻ dây CD vuông góc với OA tại M. Chứng minh:
a, Tứ giác ACOD là hình thoi.
b, Chứng minh tam giác BCD đều.
------------------------------------------------
Ngoài các dạng Toán 9 ôn thi vào lớp 10 trên, mời các bạn học sinh còn có thể tham khảo các đề thi học kì 1 lớp 9 và Đề thi vào lớp 10 môn Toán mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt!










