Bất đẳng thức tam giác: Công thức, bổ đề mở rộng và bài tập có đáp án chi tiết
Bài tập Toán 9: Bất đẳng thức trong tam giác - Có đáp án chi tiết
Bất đẳng thức tam giác là một kiến thức quan trọng trong chương trình Toán trung học, đặc biệt phổ biến trong các bài toán hình học và đại số liên quan đến độ dài đoạn thẳng. Việc hiểu rõ định nghĩa, công thức, cũng như biết cách vận dụng các bổ đề mở rộng sẽ giúp học sinh giải bài hiệu quả hơn. Trong bài viết này, chúng tôi tổng hợp đầy đủ kiến thức về bất đẳng thức tam giác, bao gồm công thức chuẩn, bổ đề áp dụng trong nhiều trường hợp và hệ thống bài tập minh họa, bài luyện tập có đáp án chi tiết, giúp học sinh ôn tập toàn diện và nâng cao kỹ năng giải toán.
A. Bất đẳng thức trong tam giác
Công thức bất đẳng thức tam giác
![]()
B. Bổ đề mở rộng bất đẳng thức tam giác trong hình học
a) Với 3 điểm ![]() bất kỳ ta luôn có:
bất kỳ ta luôn có: ![]() .
.
Dấu bằng xảy ra khi và chỉ khi ![]() thẳng hàng và điểm
thẳng hàng và điểm ![]() nằm giữa hai điểm
nằm giữa hai điểm ![]() .
.
b) Với 3 điểm ![]() bất kỳ ta luôn có:
bất kỳ ta luôn có: ![]() .
.
Dấu bằng xảy ra khi và chỉ khi ![]() thẳng hàng và điểm
thẳng hàng và điểm ![]() nằm giữa hai điểm
nằm giữa hai điểm ![]() .
.
c) Cho hai điểm ![]() nằm về một phía đường thẳng
nằm về một phía đường thẳng ![]() . Điểm
. Điểm ![]() chuyển động trên đường thẳng
chuyển động trên đường thẳng ![]() . Gọi
. Gọi  là điểm đối xứng với
là điểm đối xứng với ![]() qua
qua ![]() . Ta có kết quả sau:
. Ta có kết quả sau:
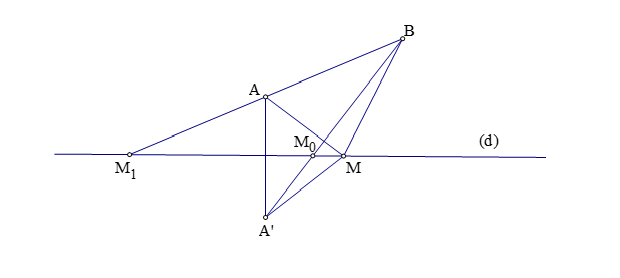
+  . Dấu bằng xảy ra khi và chỉ khi
. Dấu bằng xảy ra khi và chỉ khi ![]() là giao điểm cuả
là giao điểm cuả  và đường thẳng
và đường thẳng ![]() .(
.( ![]() trùng với
trùng với ![]() )
)
+ ![]() . Dấu bằng xảy ra khi và chỉ khi
. Dấu bằng xảy ra khi và chỉ khi ![]() là giao điểm cuả
là giao điểm cuả ![]() và đường thẳng
và đường thẳng ![]() (
( ![]() trùng với
trùng với ![]() ).
).
d) Cho hai điểm ![]() nằm về hai phía đường thẳng
nằm về hai phía đường thẳng ![]() . Điểm
. Điểm ![]() chuyển động trên đường thẳng
chuyển động trên đường thẳng ![]() . Gọi
. Gọi  là điểm đối xứng với
là điểm đối xứng với ![]() qua
qua ![]() . Ta có kết quả sau:
. Ta có kết quả sau:
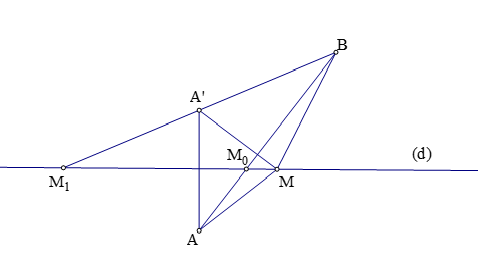
+ ![]() . Dấu bằng xảy ra khi và chỉ khi
. Dấu bằng xảy ra khi và chỉ khi ![]() là giao điểm cuả
là giao điểm cuả ![]() và đường thẳng
và đường thẳng ![]() .(
.( ![]() trùng với
trùng với ![]() )
)
+  . Dấu bằng xảy ra khi và chỉ khi
. Dấu bằng xảy ra khi và chỉ khi ![]() là giao điểm cuả
là giao điểm cuả  và đường thẳng
và đường thẳng ![]() (
( ![]() trùng với
trùng với ![]() ).
).
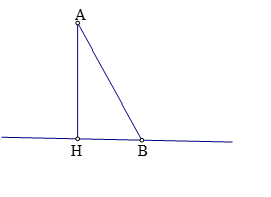
e) Trong quá trình giải toán ta cần lưu ý tính chất: Đường vuông góc luôn nhỏ hơn hoặc bằng đường xiên.
Trong hình vẽ: ![]()
C. Bài tập minh họa bất đẳng thức tam giác (có lời giải chi tiết)
Bài 1: Cho tam giác ABC và điểm M nằm trong tam giác. Chứng minh rằng:
a. MB + MC < AB + AC
b. ![]()
c. BM + MN + NC < AB + AC trong đó điểm N nằm trong tam giác sao cho MN cắt hai cạnh AB, AC.
Hướng dẫn giải:
Hình vẽ minh họa
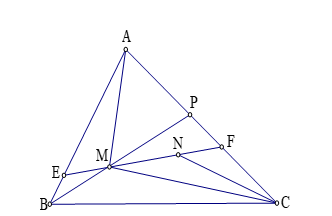
a. Đường thẳng BM cắt AC ở P.
Áp dụng bất đẳng thức (1) ta có:
MB + MC < MB + MP + PC
= BP + PC < AB + AP + PC = AB + AC
b. Theo trên ta có:
![]() .
.
Cộng theo từng vế các BĐT trên ta có điều phải chứng minh.
c. Áp dụng câu 1) ta có: ![]()
![]() .
.
Bài 2: Cho tam giác ABC và 3 trung tuyến ![]() . Chứng minh rằng:
. Chứng minh rằng:
a. ![]()
b. ![]()
c. Giả sử ![]() . Gọi
. Gọi ![]() theo thứ tự là đường phân giác, đường trung tuyến của tam giác
theo thứ tự là đường phân giác, đường trung tuyến của tam giác ![]() . Chứng minh rằng:
. Chứng minh rằng:
d. ![]()
Hướng dẫn giải:
Hình vẽ minh họa
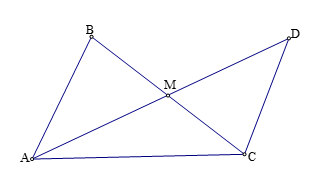
a) Xét các tam giác ![]() ta có:
ta có:
![]()
Suy ra ![]()
![]()
Gọi D là điểm đối xứng với A qua M thì ABDC là hình bình hành nên AB = CD và AD = 2AM.
Trong tam giác ACD ta có: ![]()
Như vậy: ![]() .
.
b) Áp dụng bất đẳng thức ở câu a) cho 3 đường trung tuyến AM, BN, CP ta có:
![]() ,
,
![]() ,
,
![]() .
.
Cộng ba bất đẳng thức cùng chiều ta có:
![]() .
.
c) Trong tam giác ABD; ADC có AB < AD + BD; AC < AD + DC.
Cộng theo từng vế hai BĐT trên được:AB + AC < 2AD + BC.
![]()
Kết quả này vẫn đúng với D là điểm bất kỳ nằm bên trong đoạn BC.
Dựng ![]() .
.
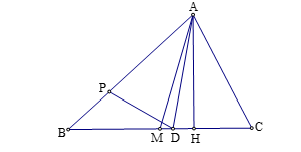
Với AB = AC thì AM = AD. Với AB > AC thì BH > CH
![]() thuộc đoạn BH.
thuộc đoạn BH.
Hơn nữa ![]() tù. Do đó D thuộc đoạn BH..
tù. Do đó D thuộc đoạn BH..
Lấy điểm P trên AB sao cho ![]() (c.g.c)
(c.g.c)
![]() .
.
+ Nếu ![]() (hình) thì
(hình) thì ![]()
=> BD > PD = CD => BM < BD => MH > DH => AM > AD.
+ Nếu ![]() (hình) thì
(hình) thì ![]()
=> BD > PD = CD => BM < BD => MH >DH => AM > AD.
Bài tập 3: Cho tam giác ABC có chu vi 2p = a + b + c (a; b; c là độ dài các cạnh của tam giác). Chứng minh rằng: ![]() ?
?
Hướng dẫn giải
Ta có: 
Áp dụng bất đẳng thức ![]() ta được:
ta được:
![]()
Tương tự: ![]() và
và ![]()
![]()
Hay ![]()
Vậy ta có điều phải chứng minh.
Dấu '' = '' xảy ra khi: ![]()
Khi đó tam giác ABC là đều.
D. Bài tập tự luyện bất đẳng thức tam giác có đáp án
Bài 1: Cho tam giác nhọn ABC có trực tâm là điểm H. Chứng minh rằng: ![]()
Bài 2: Cho tam giác đều ABC có cạnh bằng 3a. M là một điểm tùy ý trên cạnh BC, gọi P; Q lần lượt là hình chiếu vuông góc của M lên AB, AC. Tìm vị trí điểm M để:
a. PQ có độ dài nhỏ nhất
b. Dựng một đường thẳng song song với BC cắt AB, AC tại E; F sao cho AE = 2a.Tìm vị trí điểm M sao cho MA + ME + MF nhỏ nhất
Bài 3: Cho tam giác ABC có ![]() . Trên cạnh BC lấy điểm I cố định. Tìm trên cạnh AB, AC lấy hai điểm M, N để chu vi tam giác IMN đạt giá trị nhỏ nhất.
. Trên cạnh BC lấy điểm I cố định. Tìm trên cạnh AB, AC lấy hai điểm M, N để chu vi tam giác IMN đạt giá trị nhỏ nhất.
Bài 4: Cho tam giác ABC điểm M thuộc cạnh AB
a) So sánh MC với AM + AC.
b) Chứng minh MB + MC < AB + AC.
Bài 5: Cho ∆ABC. Gọi M, N, K lần lượt là 3 điểm bất kì thuộc 3 cạnh của tam giác (không trùng với đỉnh). Chứng minh chu vi ![]() bé hơn chu vi tam giác ABC.
bé hơn chu vi tam giác ABC.
Bài 6: Cho tam giác ABC có (AB < AC) và AD là phân giác góc A ![]() . Gọi E là một điểm bất kỳ thuộc cạnh AD (E khác A ). Chứng minh AC - AB > EC - EB.
. Gọi E là một điểm bất kỳ thuộc cạnh AD (E khác A ). Chứng minh AC - AB > EC - EB.
Bài 7: a) Trên hai nửa mặt phẳng đối nhau có bờ là đường thẳng ![]() , cho hai điểm
, cho hai điểm ![]() và
và ![]() không thuộc đường thẳng m . Xác định vị trí điểm N sao cho NA + NB có giá trị bé nhất.
không thuộc đường thẳng m . Xác định vị trí điểm N sao cho NA + NB có giá trị bé nhất.
b) Trên cùng một nửa mặt phẳng có bờ là đường thẳng n, cho 2 điểm phân biệt C; D không thuộc đường thẳng n. Xác định vị trí điểm M sao cho MC + MD có giá trị bé nhất.
Đáp án bài tập tự rèn luyện
Bài tập 1
Hình vẽ minh họa:
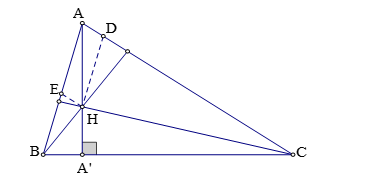
Dựng đường thẳng qua H song song với
AB cắt AC tại D. Dựng đường thẳng qua H song song AC cắt AB tại E.
Tứ giác AEHD là hình bình hành nên AD = HE; AE = HD
Xét tam giác AHD ta có: HA < HD + AD ⇔ HA < AE + AD (1) .
Vì HE // AC mà ![]() .
.
Trong tam giác vuông HBE ta có: HB < BE (2)
Tương tự ta có: HC < DC (3).
Cộng các bất đẳng thức cùng chiều (1); (2); (3) ta suy ra:
HA + HB + HC < (AE + EB) + (AD + DC) = AB + AC
Tương tự ta cũng có:
HA + HB + HC < AC + BC; HA + HB + HC < AB + BC
Suy ra ![]() .
.
Bài 2.
Hình vẽ minh họa
a) Hạ ![]() . Ta có
. Ta có
![]()
![]()
![]()
Áp dụng hệ thức lượng trong các tam giác vuông ![]() ta tính được:
ta tính được:
![]()
![]() .
.
Vì ![]() . Nên PQ nhỏ nhất bằng HK khi và chỉ khi
. Nên PQ nhỏ nhất bằng HK khi và chỉ khi ![]() là trung điểm của BC
là trung điểm của BC
b. Gọi R là điểm đối xứng với E qua BC, I là trung điểm của BC.
Ta dễ chứng minh được R; I; F thẳng hàng. Ta tính đươc:  .
.
Ta có: ![]() .
.
Dấu bằng xảy ra khi và chỉ khi ![]() . Ta cũng có
. Ta cũng có ![]() .
.
Dấu bằng xảy ra khi và chỉ khi ![]() .
.
Suy ra ![]() .
.
Dấu bằng xảy ra khi và chỉ khi ![]()
Bài 3.
Hình vẽ minh họa
Gọi E; F lần lượt là các điểm đối xứng của
I qua AB, AC. Do tam giác ABC cố định nên E; F cố định:
Ta có:
Chu vi tam giác IMN là ![]()
![]() .
.
Dấu bằng xảy ra khi và chỉ khi E; M; N; F thẳng hàng. Hay M, N là các giao điểm của EF với các cạnh AB, AC
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
--------------------------------------
Qua bài viết, bạn đã nắm được những kiến thức trọng tâm về bất đẳng thức tam giác, từ công thức cơ bản đến các bổ đề mở rộng, cùng với hệ thống bài tập đa dạng và có đáp án chi tiết. Hãy luyện tập thường xuyên, nắm chắc bản chất và kỹ năng trình bày lời giải rõ ràng để đạt kết quả cao trong các kỳ kiểm tra và kỳ thi quan trọng. Đừng quên theo dõi website để cập nhật thêm nhiều chuyên đề Toán học lớp 9, lớp 10, luyện thi THPT và ôn thi học sinh giỏi nhé!











