Xác định tâm đường tròn nội tiếp, đường tròn ngoại tiếp tam giác và đường tròn ngoại tiếp tứ giác
Chuyên đề luyện thi vào 10: Tâm đường tròn nội tiếp, đường tròn ngoại tiếp tam giác và đường tròn ngoại tiếp tam giác
Bài toán xác định tâm đường tròn ngoại tiếp, đường tròn nội tiếp tam giác hay tâm đường tròn ngoại tiếp tứ giác là một dạng toán thường có trong các đề thi tuyển sinh vào lớp 10 môn Toán gần đây. Tài liệu được VnDoc biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo chi tiết và tải về bài viết dưới đây nhé.
I. Cách xác định tâm của đường tròn
1. Xác định tâm của đường tròn ngoại tiếp tam giác
+ Tâm của đường tròn ngoại tiếp tam giác là giao điểm ba đường trung trực của ba cạnh tam giác
+ Trong tam giác vuông, trung điểm của cạnh huyền chính là tâm của đường tròn ngoại tiếp tam giác vuông ấy
2. Xác định tâm của đường tròn nội tiếp tam giác
+ Tâm của đường tròn nội tiếp tam giác là giao điểm ba đường phân giác kẻ từ 3 đỉnh của tam giác
3. Xác định tâm của đường tròn ngoại tiếp tứ giác
+ Tứ giác có bốn đỉnh các đều một điểm. Điểm đó là tâm đường tròn ngoại tiếp tam giác
+ Lưu ý: Quỹ tích các điểm nhìn đoạn thẳng AB dưới một góc vuông là đường tròn đường kính AB
II. Bài tập ví dụ cho các bài tập về tâm của đường tròn
Bài 1: Tính diện tích tam giác đều nội tiếp đường tròn (O; 2cm)?
Hướng dẫn giải
Hình vẽ minh họa
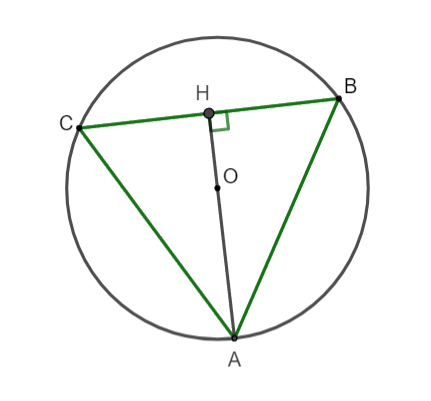
Gọi tam giác ABC đều cạnh a nội tiếp (O;2cm)
Khi đó O là trọng tâm tam giác ABC và cũng là tâm đường tròn ngoại tiếp tam giác ABC nên AO = 2cm.
Gọi AH là đường trung tuyến ![]()
![]()
Theo định lý Pytago ta có![]()
Từ đó ta có ![]()
Diện tích tam giác ABC là ![]()
Bài 2: Trong một khu vui chơi có dạng hình tam giác đều có cạnh bằng 60 m, người ta muốn tìm một vị trí đặt bộ phát sóng wifi sao cho ở chỗ nào trong khu vui chơi đó đều có thể bắt được sóng. Biết rằng bộ phát sóng đó có tầm phát sóng tối đa 50 m, hỏi rằng có thể tìm được vị trí để đặt bộ phát sóng như vậy hay không?
Hướng dẫn giải
Hình vẽ minh họa
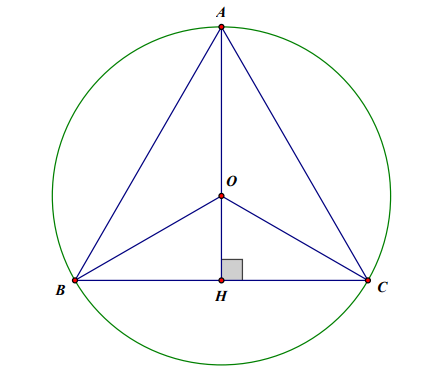
Để vị trí của bộ phát sóng wifi sao cho ở chỗ nào trong khu vui chơi đó đều có thể bắt được sóng thì bộ phát sóng wifi đặt ở tâm đường tròn ngoài tiếp tam giác khu vui chơi đó Xét khu vui chơi hình tam giác đều là tam giác ABC có cạnh 60m.
Xét đường tròn tâm (O) ngoại tiếp tam giác ABC đó. Vẽ đường cao AH của tam giác ABC.
Tam giác ABC đều nên AH vừa là đường trung trực, vừa là đường trung tuyến của tam giác.
Bán kính đường tròn ngoại tiếp ∆ABC là ![]()
Vì ![]() nên bộ phát sóng đó đặt ở tâm đường tròn ngoại tiếp tam giác thì cả khu vui chơi đều có thể bắt sóng được.
nên bộ phát sóng đó đặt ở tâm đường tròn ngoại tiếp tam giác thì cả khu vui chơi đều có thể bắt sóng được.
Bài 3: Từ một điểm A ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến AB; AC với đường tròn BC là các tiếp điểm). Trên AO lấy điểm M sao cho AM = AB. Các tia BM và CM lần lượt cắt đường tròn tại một điểm thứ hai là D và E. Chọn câu đúng.
A. M là tâm đường tròn ngoại tiếp tam giác OBC.
B. DE là đường kính của đường tròn (O).
C. M là tâm đường tròn nôi tiếp tam giác OBC.
Hướng dẫn giải
Hình vẽ minh họa
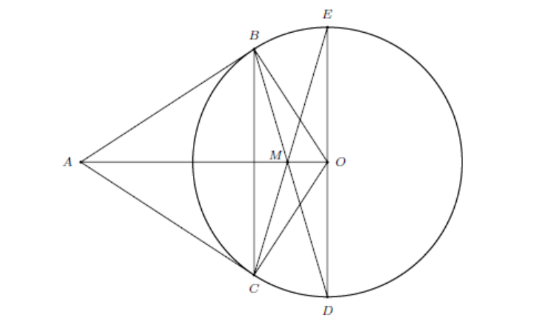
Tam giác ABM có AB = AM nên ![]() cân tại
cân tại ![]()
Ta có: ![]() nên
nên 
Từ (1) và ![]() .
.
Tương tự ![]() .
.
Điểm M là giao điểm hai đường phân giác của tam giác OBC nên M là tâm đường tròn nội tiếp tam giác OBC.
Vì tam giác BOD cân tại ![]() mà
mà ![]() nên
nên ![]() .
.
Mà hai góc này ở vị trí so le trong nên OD // BC, D, O, E thẳng hàng.
Vậy DE là đường kính của đường tròn (O).
Bài 4: Chứng minh tứ giác ABCD ngoại tiếp đường tròn khi và chỉ khi AB + CD = AD + BC.
Hướng dẫn giải
* Chứng minh chiều thuận: Nếu ABCD ngoại tiếp đường tròn thì AB + CD = AD + BC.
Hình vẽ minh họa
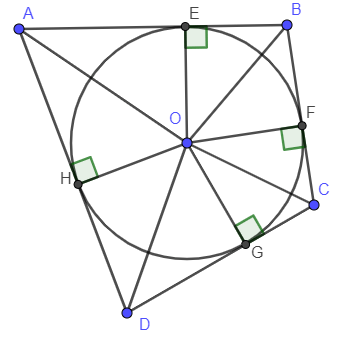
Gọi O là tâm đường tròn nội tiếp tứ giác ABCD. Vẽ OE, OF, OG, OH theo thứ tự vuông góc với AB, BC, CD, AD tại E, F, G, H.
Vì OE vuông góc với AB và (O) tiếp xúc với AB tại E nên AB là tiếp tuyến của đường tròn (O)
Vì OF vuông góc với BC và (O) tiếp xúc với BC tại F nên BC là tiếp tuyến của đường tròn (O).
Hai tiếp tuyến AB và BC cắt nhau tại B do đó BE = BF (tính chất) (1)
Chứng minh tương tự ta được CF = CG; DG = DH; AH = AE (2).
Ta có: AE + EB = AB (3)
BF + CF = BC (4)
CG + GD = CD (5)
AH + DH = AD (6)
Từ (1); (2); (3); (4); (5); (6) suy ra AB+CD=AD+BC
* Chiều ngược lại: Nếu AB + CD = AD + BC thì tứ giác ABCD là tứ giác ngoại tiếp.
- Nếu AB = AD thì CD = CB.
Hình vẽ minh họa

Khi đó giao điểm I của AC với đường phân giác trong của góc B chính là tâm đường tròn nội tiếp tứ giác ABCD. Ta có điều phải chứng minh.
- Không mất tính tổng quát ta xem AB > AD.
Hình vẽ minh họa
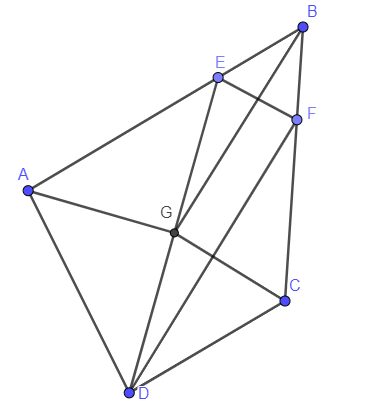
Vì AB + CD = AD + CB nên BC > CD.
Do đó tồn tại các điểm E và F theo thứ tự trên AB, BC sao cho AE = AD, CF = CD.
Ta có: AB + CD = AD + CB
=> AE + BE + CD = AD + CF + FB
=> BE = FB.
Ta có:
Tam giác ADE cân tại A do AD = AE
Tam giác BEF cân tại B do BE = BF
Tam giác CFD cân tại C do CF = CD.
Vì tam giác ADC cân tại A nên đường phân giác góc A cũng là đường trung trực của ED.
Vì tam giác BEF cân tại B nên đường phân giác góc B cũng là đường trung trực của EF.
Vì tam giác CFD cân tại C nên đường phân giác góc C cũng là đường trung trực của FD.
Mà ba điểm E, F, D không thẳng hàng nên E, F, D tạo thành một tam giác.
=> ba đường trung trực của EF, ED, FD đồng quy
Hay ba đường phân giác của ba góc của tứ giác ABCD đồng quy.
Do đó tứ giác ABCD là tứ giác ngoại tiếp.
Bài 5: Cho tam giác ABC cân tại A. Các đường cao AD, BE và CF cắt nhau tại H. Chứng minh tứ giác AEHF là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác đó.
Lời giải:
Hình vẽ minh họa
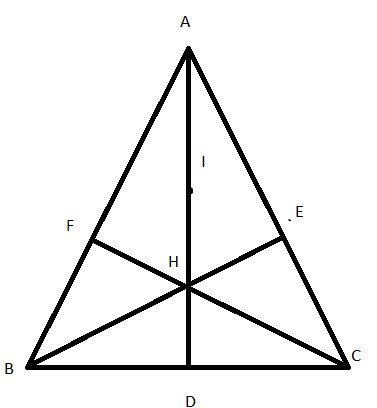
+ Gọi I là trung điểm của AH
+ Có HF vuông góc với AF (giả thiết) suy ra tam giác AFH vuông tại F
I là trung điểm của cạnh huyền AH
Suy ra IA = IF = IH (1)
+ Có HE vuông góc với AE (giả thiết) suy ra tam giác AEH vuông tại E
I là trung điểm của cạnh huyền AH
Suy ra IA = IE = IH (2)
+ Từ (1) và (2) suy ra IA = IF = IH = IE
Hay I cách đều bốn đỉnh A, E, H, F
Suy ra tứ giác AEHF nội tiếp đường tròn có tâm I là trung điểm của AH
Bài 6: Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P
a, Chứng minh tứ giác CEHD là tứ giác nội tiếp
b, Chứng minh 4 điểm B, C, E, F cùng nằm trên một đường tròn
c, Xác định tâm đường tròn nội tiếp tam giác DEF
Lời giải:
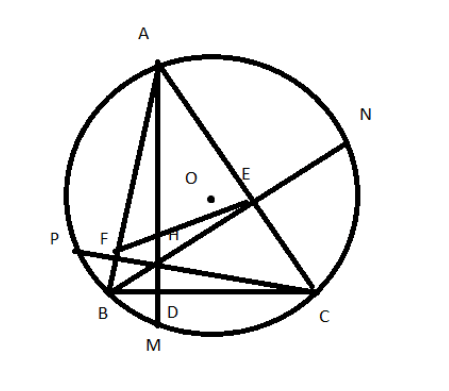
a, + Có AD là đường cao của tam giác ABC (giả thiết) ![]()
+ Có BE là đường cao của tam giác ABC (giả thiết) ![]()
+ Xét tứ giác CEHD có:
![]()
Mà hai góc ở vị trí đối nhau
Suy ra tứ giác CEHD là tứ giác nội tiếp
b, + Gọi K là trung điểm của đoạn thẳng BC
+ Xét tam giác BEC có: ![]() (BE là đường cao của tam giác)
(BE là đường cao của tam giác)
K là trung điểm của đoạn thẳng BC
Suy ra KE = KB = KC (1)
+ Xét tam giác BFC có: ![]() (CF là đường cao của tam giác)
(CF là đường cao của tam giác)
K là trung điểm của đoạn thẳng BC
Suy ra KF = KB = KC (2)
+ Từ (1), (2) suy ra KE = KB = KC = KF hay điểm K cách đều 4 điểm F, E, C, B
Suy ra tứ giác FECB nội tiếp đường tròn tâm K là trung điểm của BC
c, + Có FECB nội tiếp đường tròn ![]() (góc nội tiếp cùng chắn cung FB)
(góc nội tiếp cùng chắn cung FB)
Lại có CEHD là tứ giác nội tiếp ![]() (góc nội tiếp cùng chắn cung HD)
(góc nội tiếp cùng chắn cung HD)
Suy ra ![]() hay EB là tia phân giác của góc FED
hay EB là tia phân giác của góc FED
+ Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE
Mà BE và CF cắt nhau tại H nên H là tâm đường tròn nội tiếp tam giác DEF
III. Bài tập tự luyện các bài toán xác định tâm của đường tròn
Bài 1: Các đường cao AD, BE của tam giác ABC cắt nhau tại H (góc C khác góc vuông) và cắt đường tròn (O) ngoại tiếp tam giác ABC lần lượt tại I và K.
a, Chứng minh tứ giác CDHE nội tiếp và xác định tâm của đường tròn ngoại tiếp tứ giác đó.
b, Chứng minh tam giác CIK là tam giác cân.
Bài 2: Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O; R). Ba đường của tam giác là AF, BE và CD cắt nhau tại H. Chứng minh tứ giác BDEC là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác.
Bài 3: Cho tam giác ABC vuông tại A có AB < AC, đường cao AH (H thuộc BC). Lấy điểm D sao cho H là trung điểm của BD. Gọi E là chân đường vuông góc hạ từ C xuống đường thẳng AD. Chứng minh tứ giác AHEC nội tiếp và xác định vị trí tâm O của đường tròn ngoại tiếp tứ giác đó.
Bài 4: Cho tam giác ABC nhọn nội tiếp đường tròn (O) (AB < AC). Gọi H là giao điểm của các đường cao AI, BM, CN của tam giác ABC. Đường thẳng BC cắt đường thẳng MN tại D. Chứng minh tứ giác BNMC nội tiếp. Xác định tâm K của đường tròn này
Bài 5: Cho tam giác nhọn ABC nội tiếp đường tròn (O; R). Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H.
a, Chứng minh bốn điểm B, F, E, C cùng nằm trên một đường tròn.
b, Kẻ đường kính AK của đường tròn (O). Tứ giác BHCK là hình gì? Vì sao?
c, Chứng minh H là tâm đường tròn nội tiếp tam giác DEF.
Bài 6: Cho tam giác ABC cân tại A, AB = AC nội tiếp đường tròn tâm O. Các đường cao AQ, BE, CF cắt nhau tại một điểm.
a, Chứng minh rằng tứ giác AEHF là tứ giác nội tiếp, xác định tâm của đường tròn ngoại tiếp tứ giác đó.
b, Cho bán kính đường tròn tâm I là 2cm góc BAC = 500. Tính độ dài cung EHF của đường tròn tâm I và diện tích hình quạt tròn IEHF.
-------------------
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết: Xác định tâm đường tròn ngoại tiếp, đường tròn nội tiếp tam giác hay tâm đường tròn ngoại tiếp tứ giác.
Các dạng bài tập Toán 9 ôn thi vào lớp 10 là tài liệu tổng hợp 5 chuyên đề lớn trong chương trình Toán lớp 9, bao gồm:
- Rút gọn biểu thức - Xem thêm Ôn thi vào lớp 10 chuyên đề 1: Rút gọn và tính giá trị của biểu thức
- Hàm số đồ thị - Xem thêm Ôn thi vào lớp 10 chuyên đề 5: Hàm số và đồ thị
- Phương trình, hệ phương trình - Xem thêm Ôn thi vào lớp 10 chuyên đề 2: Giải phương trình và hệ phương trình bậc nhất hai ẩn
- Giải bài toán bằng cách lập phương trình, hệ phương trình - Xem thêm Kỹ năng giải toán bằng cách lập phương trình, hệ phương trình
- Hình học - Xem thêm Ôn thi vào lớp 10 chuyên đề 10: Chứng minh các hệ thức hình học
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Luyện thi lớp 9 lên 10 . Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.









