Đề thi thử vào 10 chuyên môn Toán (chuyên) năm 2025 lần 1 trường chuyên ĐHSP Hà Nội
Ôn thi vào lớp 10 môn Toán có đáp án
Tìm hiểu thêmTặng thêm 15 ngày khi mua gói 4 tháng.
TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI
TRƯỜNG THPT CHUYÊN
Đề thi gồm có: 01 trang
KỲ THI THỬ VÀO LỚP 10 THPT CHUYÊN
NĂM 2025 - LẦN 1
BÀI THI MÔN: TOÁN CHUYÊN
Dành cho các thí sinh thi thử vào chuyên Toán, chuyên Tin
Thời gian làm bài: 120 phút, không kể thời gian phát đề
Họ và tên thí sinh:. . .. . . . . . . . . . . . . . .
Số báo danh:. . . . . . . . . . . . . . . . . . . . . . . .
Câu 1. (2,0 điểm)
a/ Giải phương trình
√
9 − 2x
2
+
3
√
x
2
+ 4 = 3.
b/ Cho x, y, z là các số thực dương thỏa mãn 4x
2
+ y
2
= 32z
2
. Chứng minh rằng
1
x
+
2
y
−
1
z
≥ 0.
Câu 2. (1,0 điểm) Tồn tại hay không một tập hợp A khác rỗng, là tập con của tập các số tự nhiên
và thỏa mãn đồng thời các điều kiện sau?
◦ Với hai số tự nhiên phân biệt bất kỳ mà có tổng là số chẵn thì ít nhất một trong hai số đó thuộc
tập hợp A.
◦ Với hai số tự nhiên phân biệt bất kỳ mà có tổng là số lẻ thì ít nhất một trong hai số đó không
thuộc tập hợp A.
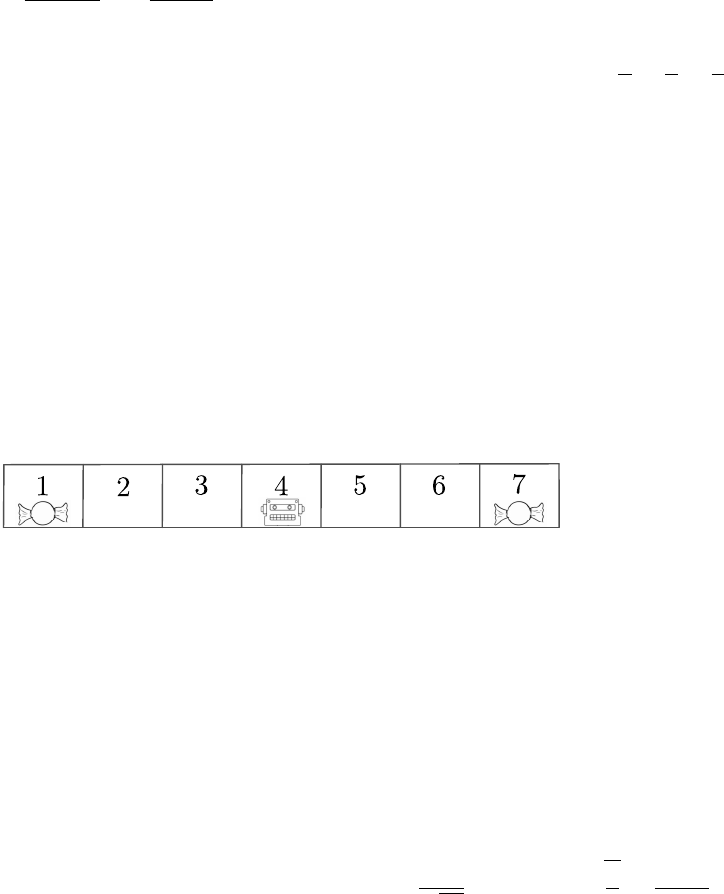
Câu 3. (1,0 điểm) Một rô-bốt di chuyển trên một bảng gồm 7 ô được đánh số từ 1 đến 7 như hình
vẽ sau.
Ban đầu, rô-bốt đứng ở ô số 4. Mỗi bước, nó có thể nhảy sang trái hoặc sang phải, mỗi hướng
có xác suất bằng nhau, và mỗi lần nhảy chỉ di chuyển đúng một ô. Tại ô số 1 và ô số 7 có đặt kẹo,
và khi rô-bốt đến một trong hai ô này, nó lấy kẹo và dừng lại. Tính xác suất để rô-bốt lấy kẹo sau
đúng 3 bước.
Câu 4. (3,0 điểm)
a/ Cho a, b là hai số nguyên trái dấu. Biết rằng phương trình x
2
+ ax + b = 0 có nghiệm nguyên và
phương trình x
2
+ bx + a = 0 có nghiệm nguyên. Chứng minh rằng a + b = −1.
b/ Tìm số nguyên z và các số hữu tỷ x, y thỏa mãn điều kiện
3
√
2x
− 1 = 1 −
r
3
y
=
z
x + y
.
Câu 5. (3,0 điểm) Cho tam giác nhọn, không cân ABC nội tiếp đường tròn (O), gọi AH, AD lần
lượt là đường cao và đường phân giác trong góc A (H, D ∈ BC). Gọi M là giao điểm của AO và
BC. Đường trung trực của đoạn thẳng AD cắt (O) tại E, F . Chứng minh rằng
a/ Trực tâm của tam giác DEF thuộc (O).
b/ Bốn điểm H, E, F, M cùng thuộc một đường tròn.
———————–Hết———————–
Chú ý. Thí sinh không được dùng tài liệu. Giám thị không giải thích gì thêm.
TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI
TRƯỜNG THPT CHUYÊN
(Hướng dẫn chấm có 04 trang)
KỲ THI THỬ VÀO LỚP 10 THPT CHUYÊN
NĂM 2025 - LẦN 1
(Dành cho thí sinh thi vào lớp chuyên Toán và chuyên Tin)
Thời gian làm bài: 120 phút, không kể thời gian phát đề
I. Hướng dẫn chung
1) Nếu học sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì cho đủ số điểm từng
phần như hướng dẫn quy định.
2) Việc chi tiết hóa (nếu có) thang điểm trong hướng dẫn chấm phải bảo đảm không làm sai
lệch hướng dẩn chấm và phải được thống nhất thực hiện trong tổ chấm.
II. Đáp án và thang điểm
Câu Nội dung Điểm
1a
(1,0
điểm)
Điều kiện xác định −
3
√
2
2
≤ x ≤
3
√
2
2
.
Đặt
√
9 − 2x
2
= a,
3
√
x
2
+ 4 = b (a ≥ 0, b > 0). Từ phương trình đã cho ta có
a + b = 3 (1)
a
2
+ 2b
3
= 17 (2)
.
(1) ⇔ a = 3 − b. Thay vào (2) ta được 2b
3
+ b
2
− 6b − 8 = 0. Phương trình này
tương đương với (b − 2)(2b
2
+ 5b + 4) = 0. Do đó b = 2.
Ta có
3
√
x
2
+ 4 = 2. Suy ra x = 2 hoặc x = −2. Thử lại thấy cả hai giá trị đều
thỏa mãn. Vậy phương trình đã cho tập nghiệm S = {−2, 2}.
1,0
1b
(1,0
điểm)
Theo đề bài, 4
x
2
z
2
+
y
2
z
2
= 32. Đặt
x
z
= t (t > 0).
Khi đó
y
z
=
√
32 − 4t
2
= 2
√
8 − t
2
.
Ta có: z
1
x
+
2
y
=
z
x
+ 2
z
y
=
1
t
+
2
2
√
8 − t
2
=
1
t
+
1
√
8 − t
2
.
Áp dụng bất đẳng thức Cauchy–Schwarz, ta có
1
t
+
1
√
8 − t
2
≥
(1 + 1)
2
t +
√
8 − t
2
=
4
t +
√
8 − t
2
. (1)
0,5
Áp dụng bất đẳng thức Bunhiacopxki, ta được
(t +
√
8 − t
2
)
2
≤ (1
2
+ 1
2
)(t
2
+ 8 − t
2
) = 16.
Suy ra t +
√
8 − t
2
≤ 4. Kết hợp với (1), ta được
1
t
+
1
√
8 − t
2
≥ 1.
Do đó z
1
x
+
2
y
≥ 1. Vậy
1
x
+
2
y
−
1
z
≥ 0.
Dấu "=" xảy ra khi t =
√
8 − t
2
⇔ t = 2. Khi đó
x
z
= 2,
y
z
= 4.
0,5
Câu Nội dung Điểm
2
(1,0
điểm)
Giả sử tồn tại tập hợp A thỏa mãn điều kiện đề bài.
Với x = 1, y = 3, ta có x + y = 4 là số chẵn. Suy ra 1 ∈ A hoặc 3 ∈ A. Xét hai
trường hợp.
Trường hợp 1. 1 ∈ A.
Với x = 1, y = 2, ta có x + y = 3 là số lẻ. Suy ra 1 /∈ A hoặc 2 /∈ A. Vì 1 ∈ A nên
2 /∈ A. Tương tự, 4 /∈ A.
Với x = 2, y = 4, ta có x + y = 6 là số chẵn. Suy ra 2 ∈ A hoặc 4 ∈ A (Mâu
thuẫn).
Trường hợp 2. 3 ∈ A. Chứng minh tương tự.
Vậy điều giả sử là sai. Do đó không tồn tại tập hợp A thỏa mãn điều kiện đề bài.
1,0
3
(1,0
điểm)
Ở mỗi ô, rô-bốt có hai sự lựa chọn để di chuyển với xác suất như nhau. Do đó số
cách di chuyển sau ba bước là 2 · 2 · 2 = 8.
Số phần tử của không gian mẫu là 8.
0,5
Có hai khả năng thuận lợi cho biến cố: "rô-bốt lấy kẹo sau đúng 3 bước" là
4 → 3 → 2 → 1 và 4 → 5 → 6 → 7.
Xác suất cần tìm là
2
8
=
1
4
.
0,5
4a
(1,5
điểm)
Không mất tính tổng quát, giả sử a > 0 > b.
Ký hiệu x
2
+ ax + b = 0 (1) và x
2
+ bx + a = 0 (2).
Nếu a > −b thì (a + 2)
2
> a
2
+ 4a > ∆
1
= a
2
− 4b > a
2
.
Do đó ∆
1
= (a + 1)
2
. Suy ra a
2
− 4b = (a + 1)
2
⇔ −4b = 2a + 1 (vô lý).
Vậy a ≤ −b.
Nếu a = −b thì ∆
1
= a
2
+ 4a = k
2
(k ∈ N
∗
). Suy ra (a + 2 − k)(a + 2 + k) = 4.
Do đó a = 0 hoặc a = −4 (loại).
0,5
Nếu a = −b − 1 thì (1) có các nghiệm là 1, b và (2) có các nghiệm là 1, a (thỏa
mãn).
Nếu a ≤ −b − 2 thì −a ≥ b + 2. Khi đó ∆
2
= b
2
− 4a ≥ b
2
+ 4(b + 2) > (b + 2)
2
.
Vì a > 0 nên ∆
2
= b
2
−4a < b
2
. Suy ra b
2
> ∆
2
> (b + 2)
2
. Do đó ∆
2
= (b + 1)
2
.
Ta có ∆
2
= b
2
− 4a = (b + 1)
2
⇔ −4a = 2b + 1 (vô lý).
Vậy a + b = −1.
1,0
Đề minh họa thi vào 10 môn Toán 2025
VnDoc giới thiệu đến quý thầy, cô giáo và các em học sinh Đề thi thử vào 10 chuyên môn Toán (chuyên) năm 2025 lần 1 trường chuyên ĐHSP Hà Nội. Tài liệu tổng hợp nhiều đề thi khác nhau có đáp án và hướng dẫn chấm điểm.
Ngoài tài liệu trên, VnDoc còn gửi tới các bạn nhiều tài liệu tuyển sinh vào lớp 10 các môn để giúp các em ôn luyện, làm quen với nhiều đề thi khác nhau, chuẩn bị cho kì thi tuyển sinh vào lớp 10 năm học 2025 - 2026.
