Chuyên đề Tứ giác nội tiếp Toán 9 (Có đáp án)
Chuyên đề Tứ giác nội tiếp Toán 9 (Có đáp án)
Chuyên đề Tứ giác nội tiếp Toán 9 được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.
- Bài tập về đường thẳng và parabol Toán 9
- 4 đề thi giữa học kì 2 môn Toán lớp 9 năm học 2019 - 2020
- Tổng hợp các dạng Toán ôn thi vào 10 - Phần 1: Đại số
Đây là phần bài tập về Tứ giác nội tiếp được chia làm hai phần: Lý thuyết và bài tập vận dụng. Phần lý thuyết được chia thành các cách chứng minh Tứ giác nội tiếp và gồm các mức độ phân loại học sinh. Phần bài tập được sưu tầm và chọn lọc để các bạn học sinh có thể áp dụng lý thuyết phía trên vận dụng làm bài. Qua đó sẽ giúp cho các bạn học sinh ôn tập và củng cố lại kiến thức về Tứ giác nội tiếp đồng thời nắm vững các kiến thức để chuẩn bị cho kì thi tuyển sinh vào lớp 10.
A. Tứ giác nội tiếp là gì?
Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên một đường tròn. Đường tròn đó được gọi là đường tròn ngoại tiếp tứ giác.
B. Cách chứng minh tứ giác nội tiếp
Phương pháp 1: Chứng minh bốn đỉnh của tứ giác cùng cách đều một điểm.
Ví dụ 1: Cho hình thang có
. Chứng minh bốn điểm
cùng thuộc một đường tròn.
Hướng dẫn giải
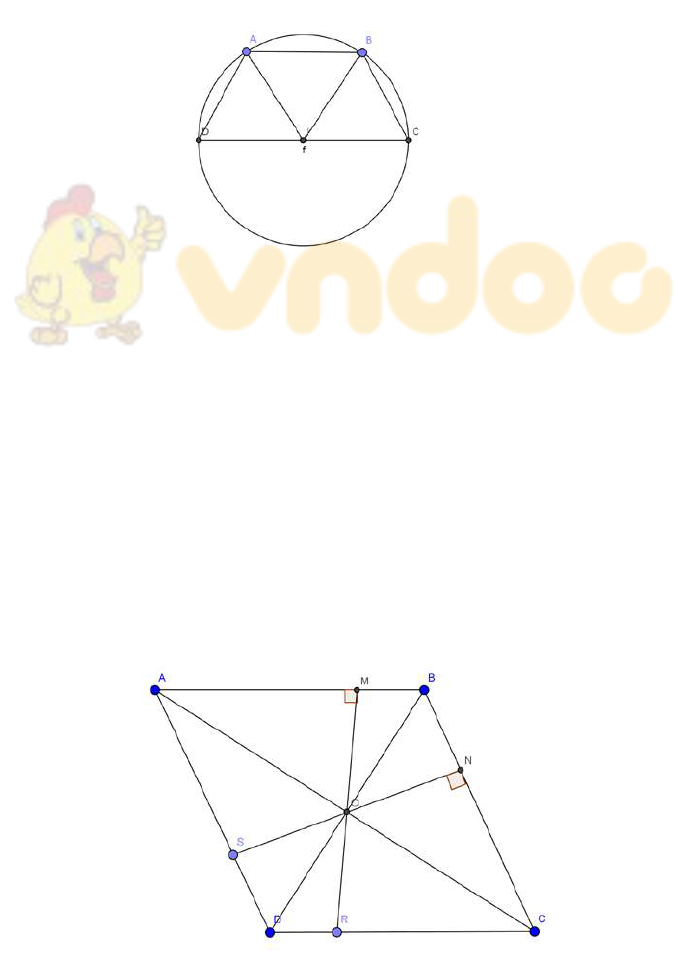
Hình vẽ minh họa
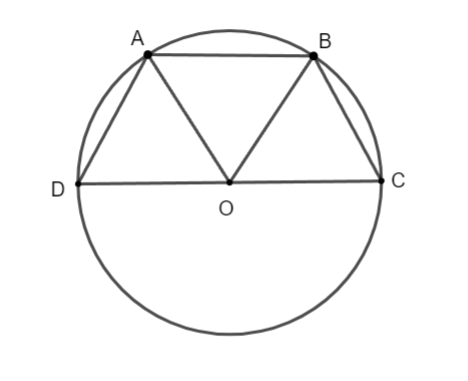
Gọi là trung điểm
, ta có
là hình hành
Tương tự
là hình thang có
nên
là hình thang cân (3)
Từ (1), (2), (3) ta có hai tam giác đều hay
hay bốn điểm
cùng thuộc một đường tròn.
Mức độ 3:
Bài 1: Cho nửa đường tròn tâm đường kính
và tia tiếp tuyến
cùng phía với nưa đường tròn đối với
. Từ điểm
trên
kẻ tiếp tuyến thứ hai
với nưa đường tròn (
là tiếp điểm).
cắt
tại
cắt nưa đường tròn
tại
khác
.
Chứng minh: và
là các tứ giác nội tiếp đường tròn.
Hướng dẫn giải
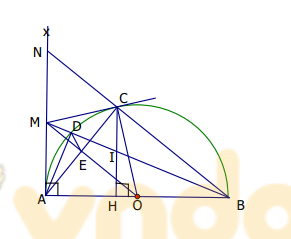
Vì là tiếp tuyến nên:
là tứ giác nội tiếp đường tròn đường kính MO.
(góc nội tiếp chắn nưa đường tròn)
(1)
Lại có: (tính chất tiếp tuyến). Suy ra
là đường trung trực của
.
Từ (1) và (2) suy ra là tứ giác nội tiếp đường tròn đường kính
.
Bài 2: Cho hai đường tròn và
cắt nhau tại
và
. Vẽ
thứ tự là đường kính của hai đường tròn
và
.
a) Chứng minh ba điểm thẳng hàng.
b) Đường thẳng cắt đường tròn
tại
; đường thẳng
cắt đường tròn
tại
khác
. Chứng minh bốn điểm
cùng nằm trên một đường tròn.
Hướng dẫn giải
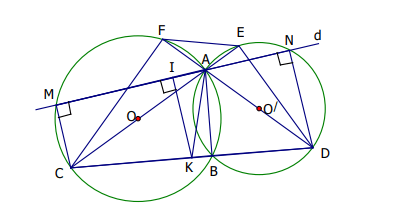
a) và
lần lượt là các góc nội tiếp chắn nửa đường tròn
và
Suy ra thẳng hàng.
b) Xét tứ giác có:
(góc nội tiếp chắn nửa đường tròn
)
(góc nội tiếp chắn nửa đường tròn
suy ra
là tứ giác nội tiếp.
Bài 3: Cho 2 đường tròn và
cắt nhau tại hai điểm
và
phân biệt. Đường thẳng
cắt
,
lần lượt tại điểm thứ hai
và
. Đường thẳng
cắt
lần lượt tại điểm thứ hai
,
.
1. Chứng minh 3 đường thẳng và
đồng quy tại một điểm I .
2. Chứng minh tứ giác nội tiếp được trong một đường tròn.
Hướng dẫn giải:
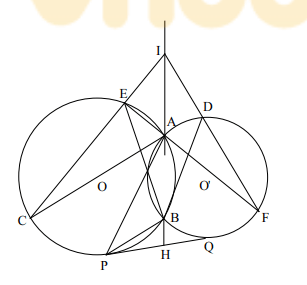
Ta có: (góc nội tiếp chắn nửa đường tròn)
(góc nội tiếp chắn nửa đường tròn) nên
thẳng hàng.
và
là 3 đường cao của tam giác
nên chúng đồng quy.
2. Do suy ra
nội tiếp đường tròn.
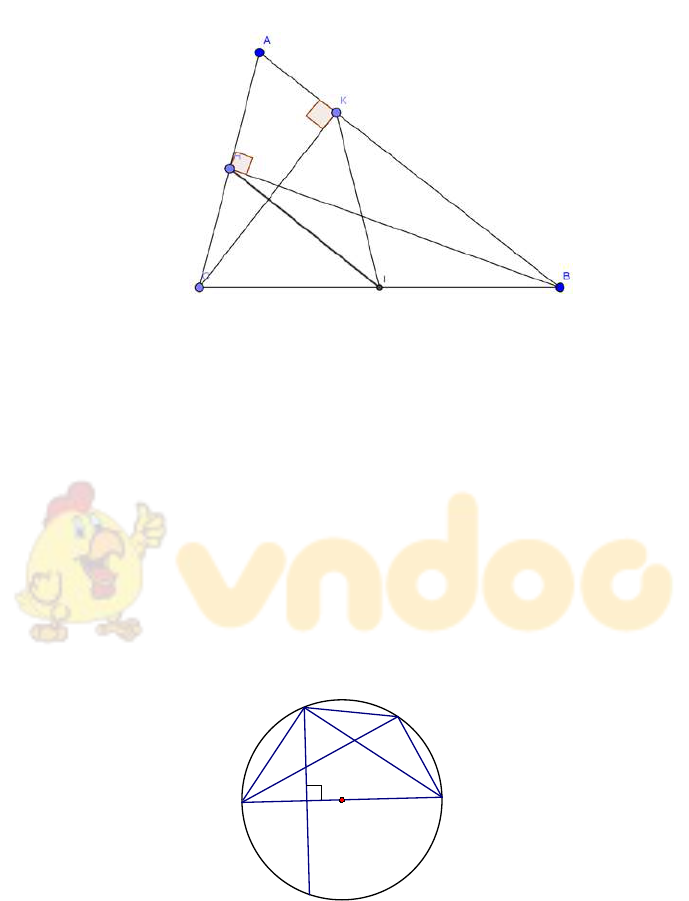
Mức độ 4:
Bài 1: Cho nửa đường tròn tâm đường kính
. Lấy điểm
thuộc đoạn thẳng
, điểm
thuộc nửa đường tròn
. Từ
và
vẽ các tiếp tuyến
và
. Đường thẳng qua V và vuông góc với
cắt
thứ tự tại
và
.
a) Chứng minh và
là các tứ giác nội tiếp đường tròn.
b) Chứng minh đồng dạng với
từ đó suy ra
là tứ giác nội tiếp.
Hướng dẫn giải
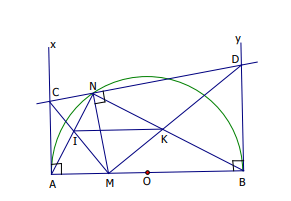
a) Ta có tứ giác có:
(tính chất tiếp tuyến).
là tứ giác nội tiếp đường tròn đường kính
. Tương tự tứ giác
nội tiếp đường tròn đường kính.
b) và
có:
(do tứ giác
nội tiếp)
(do tứ giác
nội tiếp ) nên
(g.g)
c) (do
là góc nội tiếp chắn nửa đường tròn
)
Suy ra là tứ giác nội tiếp đường tròn đường kính
Phương pháp 2: Chứng minh tứ giác có hai góc đối diện bù nhau (tổng hai góc đối diện bằng 1800.
Ví dụ 2: Cho nữa đường tròn tâm đường kính
, điểm
bất kì trên nửa đường tròn (
khác
). Trên nửa mặt phẳng bờ
chứa nửa đường tròn kẻ tiếp tuyến
. Tia
cắt
tại
; tia phân giác của góc
cắt nửa đường tròn tại
; cắt tia
tại
tia
cắt
tại
, cắt
tại
. Chứng minh rằng:
là tứ giác nội tiếp.
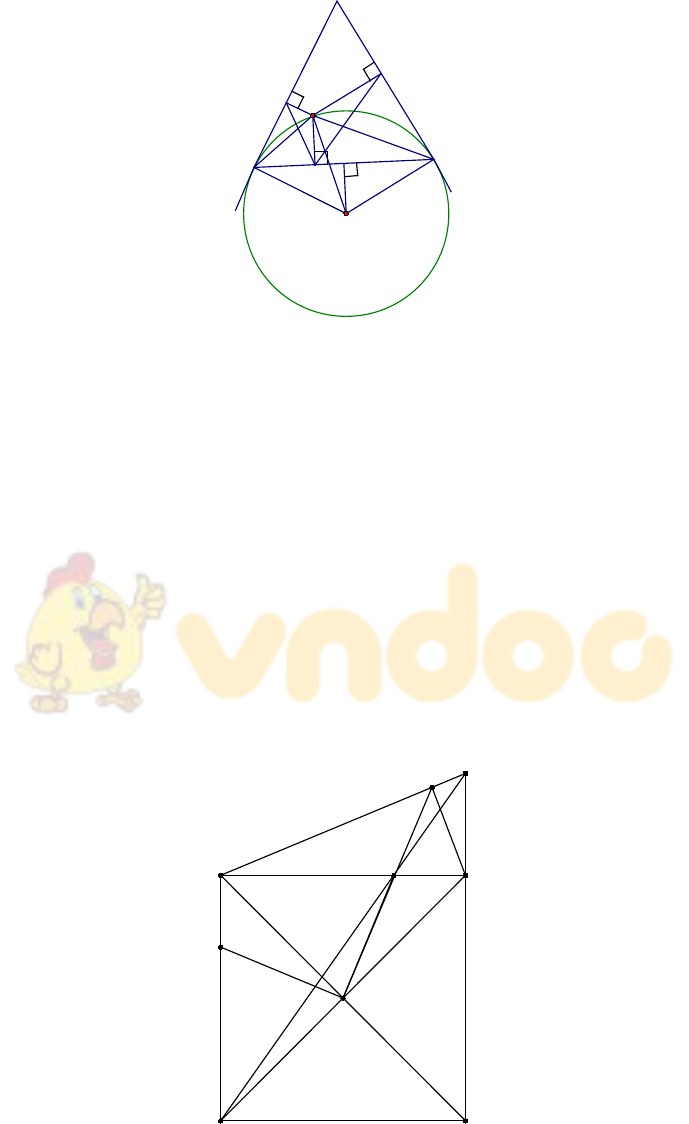
Hướng dẫn giải
Hình vẽ minh họa
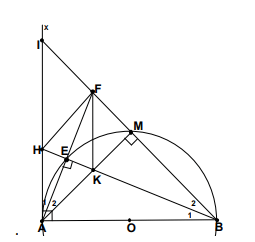
Ta có: (nội tiếp chắn nửa đường tròn)
(vì là hai góc kề bù).
(nội tiếp chắn nửa đường tròn)
(vì là hai góc kề bù).
do đó
là tứ giác nội tiếp.
Phương pháp 3: Chứng minh hai đỉnh cùng nhìn đoạn thẳng tạo bởi hai điểm còn lại hai góc bằng nhau.
Ví dụ 3: Từ một điểm nằm ngoài đường tròn
ta vẽ hai tiếp tuyến
với đường tròn (
là tiếp điểm). Trên cung nhỏ
lấy một điểm M và
a) Chứng minh: AIMK là tứ giác nội tiếp đường tròn.
b) Vẽ . Chứng minh:
.
Hướng dẫn giải
Hình vẽ minh họa
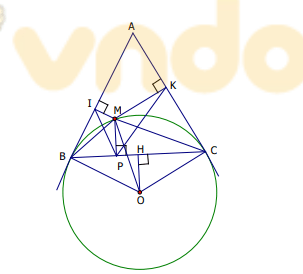
a. Ta có (giả thiết)
Suy ra tứ giác AIMK là tứ giác nội tiếp đường tròn đường kính AM
b. Tứ giác CPMK có (giả thiết). Do đó CPMK là tứ giác nội tiếp
(1)
Vì KC là tiếp tuyến của (O) nên ta có: (cùng chắn cung MC) (2)
Từ (1) và (2) suy ra (3)
Chứng minh tương tự câu b ta có BPMI là tứ giác nội tiếp.
--------------------------------------------------
Ngoài Chuyên đề Tứ giác nội tiếp, mời các bạn học sinh tham khảo thêm các đề thi học kì 2 Toán 9, đề cương ôn tập các môn Toán 9 học kì 2,... mà chúng tôi đã sưu tầm và chọn lọc. Với bài tập về chuyên đề Tứ giác nội tiếp này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tập tốt!






