VnDoc.com

Tài liệu ôn thi vào lớp 10 môn Toán

Đề ôn thi vào lớp 10 môn Toán

VẤN ĐỀ 1. RÚT GỌN BIỂU THỨC CÓ CHỨA CĂN

A. PHƯƠNG PHÁP GIẢI TOÁN

Bài toán 1.1 Cho biểu thức

2

1 1

x x x x

P

x x x

 

 

  

với

0, 1.

x x

 

a) Rút gọn biểu thức P

b) Tìm x khi

0.

P



(Trích đề thi tuyển sinh vào lớp 10 tỉnh Nam Định năm 2011)

 Lời giải. a) Với

0, 1

x x

 

ta có

   





 

3

1

1 1 1

1 1 1 1

x x

x x x x x x x

P

x x x x x x

 



  

 

 

   

     









 

1 1

1

x x x x

x x

  

    

 

2 .

x x x x x

    

Vậy với

0, 1

x x

 

thì

2 .

P x x

 

b) Với

0, 1

x x

 

ta có





0 2 0 2 0

P x x x x

      

0

0 0

4

2

2 0

x

x x

x







 



  





 







Đối chiếu với điều kiện

0, 1

x x

 

ta thấy hai giá trị này đều thỏa mãn.

Vậy với

0

P



thì

0, 4.

x x

 

NHỮNG ĐIỂM CẦN LƯU Ý KHI GIẢI TOÁN

Kĩ năng cũng như cách giải chung cho dạng toán như câu a

 Đặt điều kiện thích hợp, nếu đề bài đã nêu điều kiện xác định thì ta vẫn phải chỉ

ra trong bài làm của mình như lời giải nêu trên.

 Đa phần các bài toán dạng này, chúng ta thường quy đồng mẫu, xong rồi tính toán

rút gọn tử thức và sau đó xem tử thức và mẫu thức có thừa số chung nào hay

không để rút gọn tiếp.

 Trong bài toán trên thì đã không quy đồng mẫu mà đơn giản biểu thức luôn.

 Khi làm ra kết quả cuối cùng, ta kết luận giống như trên.

Đối với dạng toán như câu b

 Cách làm trên là điển hình, không bị trừ điểm.

 Ngoài câu hỏi tìm x như trên thì người ta có thể hỏi: cho x là một hằng số nào đó

bắt rút gọn P, giải bất phương trình, tìm giá trị lớn nhất nhỏ nhất, tìm x để P có

giá trị nguyên, chứng minh một bất đẳng thức. Nhưng thường thì người ta sẽ hỏi

như sau: tìm x để P có giá trị nào đó (như ví dụ nêu trên), cho x nhận một giá trị

cụ thể để tính P.

MỘT SỐ CÂU HỎI MỞ CHO BÀI TOÁN

 Câu hỏi mở 1. Rút gọn P khi

3 2 2.

x  

Ta có

2 2 2

3 2 2 1 2.1. 2 ( 2) (1 2)

x       

Khi đó, với

0, 1

x x

 

thì

2

(1 2) 1 2

x    

Do đó

2 3 2 2 2(1 2) 3 2 2 2 2 2 1.

P x x

          

Vậy với

3 2 2

x  

thì

1.

P



 Câu hỏi mở 2. Tìm giá trị nhỏ nhất của P

Với

0, 1

x x

 

ta có

2 2

2 ( ) 2 1 1 ( 1) 1

P x x x x x

        

Vì

1

x



nên

2

( 1) 0

x

 

2

( 1) 1 1

x

    

Vậy với

0, 1

x x

 

thì P không có giá trị nhỏ nhất.

Trong loại câu hỏi này, ta cần chú ý đến điều kiện xác định. Chẳng hạn với điều kiện

4

x



ta rút gọn được

P x x

  thì ta sẽ không làm như trên mà sẽ làm như sau

Với

4

x



ta có 2 ( 2)

P x x x x x x

     

Vì

4 2 0, 2 0 ( 2) 0 2 2

x x x x x x x

            

Vậy

min 2

P



, dấu bằng xảy ra khi và chỉ khi

4

x



(thỏa mãn điều kiện).

 Câu hỏi mở 3. Chứng minh rằng

1

P

 

thì ta làm như trên nhưng kết luận là

1.

P

 

 Câu hỏi mở 4. Tìm số nguyên x để P có giá trị nguyên.

Ví dụ trên, ta có

2

P x x

  , thì thường đề bài sẽ không hỏi đến nghiệm nguyên. Chẳng

hạn với điều kiện

1

x



ta rút gọn được

3

1

x

P

x





, đề bài hỏi: tìm số nguyên x để P nhận

giá trị nguyên thì ta làm như sau

Với

1

x



, ta có

3 3( 1) 3 3

3

1 1 1

x x

P

x x x

 

   

  

Từ đó với x là số nguyên,

3 3

3 3 ( 1)

1 1

P x

x x

      

 

¢ ¢ M

Tương đương với

1

x



là ước của 3, mà ước của 3 là









3; 1;1;3 ( 1) 3; 1;1;3

x      

Ta xét thêm một bài toán nữa là một câu trong đề chung chuyên Lê Hồng Phong Nam

Định năm 2011.

Mà

x 1 x1 2  x1 3 x  2

(thỏa mãn điều điện)

Kết luận: vậy

x  2

là giá trị cần tìm.

Bài toán 1.2 Cho biểu thức

3 1 1 1

:

1

x

P

x

x x x

 



 

 



 

 

với

0, 1.

x x

 

a) Rút gọn biểu thức B

b) Tìm x để

2 3.

P x

 

(Đề chung Chuyên Lê Hồng Phong Nam Định năm 2011)

 Lời giải. a) Với

0, 1

x x

 

ta có

 

3 1 1

( 1)( 1) ( 1)( 1)

x x

B x x

x x x x

 

 

  

 

   

 

3 1 1

( 1).

( 1)( 1)

x x

  

 

 

(2 2) 2 ( 1)

2 .

1 1

x x x x

x

x x

 

  

 

Vậy với

0, 1

x x

 

thì

2 .

P x



b) Với

0, 1

x x

 

và

2

P x

 ta có

2 3 4 3

4 3 0

3 3 0

( 1) 3( 1) 0

( 1)( 3) 0

1 0 1 1

9

3 0 3

P x x x

x x

x x x

x x

x x x

x

x x

    

   

    

    

   

 

   



  

 





  



 

 

Kết hợp với điều kiện nêu trên thì chỉ có

9

x



thỏa mãn bài toán.

B. CÁC BÀI TOÁN RÈN LUYỆN

Bài 1: Cho biểu thức











6

5

3

2

aaa

a

P

a2

1

a) Rút gọn P.

b) Tìm giá trị của a để

1.

P



Bài 2: Cho biểu thức P =









































65

2

3

2

3

:

1

xx

x

a) Rút gọn P.

b) Tìm giá trị của x để

0.

P



Ôn thi vào lớp 10 môn Toán

Tài liệu ôn thi vào lớp 10 môn Toán là tài liệu ôn thi vào lớp 10 tham khảo cho các bạn học sinh lớp 9. Tài liệu ôn thi vào lớp 10 môn Toán này do thầy Vũ Văn Bắc biên soạn, dành cho các bạn học sinh lớp 9 nghiên cứu, hệ thống củng cố kiến thức Toán 9 cũng như luyện đề, bài tập nhằm có các cách giải toán được nhanh nhất, thông minh nhất, giúp các bạn ôn thi môn Toán vào lớp 10 được hiệu quả cao.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

VẤN ĐỀ 1. RÚT GỌN BIỂU THỨC CÓ CHỨA CĂN

A. PHƯƠNG PHÁP GIẢI TOÁN

Bài toán 1.1 Cho biểu thức:

a) Rút gọn biểu thức P

b) Tìm x khi P = 0

(Trích đề thi tuyển sinh vào lớp 10 tỉnh Nam Định năm 2011)

Lời giải:

Tài liệu ôn thi vào lớp 10 môn Toán

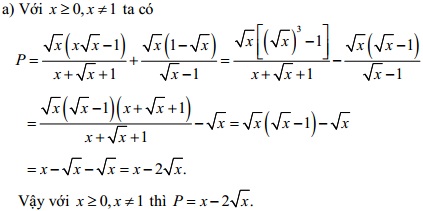
b) Với x ≥ 0, x ≠ 1 ta có

P = 0 ↔ x - 2√x = 0 ↔ √x.(√x - 2) = 0 ↔ √x = 0 hoặc √x - 2 = 0 ↔ x = 0 hoặc √x = 2 ↔ x = 0 hoặc x = 4

Đối chiếu với điều kiện x ≥ 0, x ≠ 1 ta thấy hai giá trị này đều thỏa mãn.

Vậy với P = 0 thì x = 0, x = 4.

NHỮNG ĐIỂM CẦN LƯU Ý KHI GIẢI TOÁN:

* Kĩ năng cũng như cách giải chung cho dạng toán như câu a

Đặt điều kiện thích hợp, nếu đề bài đã nêu điều kiện xác định thì ta vẫn phải chỉ ra trong bài làm của mình như lời giải nêu trên.
Đa phần các bài toán dạng này, chúng ta thường quy đồng mẫu, xong rồi tính toán rút gọn tử thức và sau đó xem tử thức và mẫu thức có thừa số chung nào hay không để rút gọn tiếp.
Trong bài toán trên thì đã không quy đồng mẫu mà đơn giản biểu thức luôn.
Khi làm ra kết quả cuối cùng, ta kết luận giống như trên.

* Đối với dạng toán như câu b

Cách làm trên là điển hình, không bị trừ điểm.
Ngoài câu hỏi tìm x như trên thì người ta có thể hỏi: cho x là một hằng số nào đó bắt rút gọn P, giải bất phương trình, tìm giá trị lớn nhất nhỏ nhất, tìm x để P có giá trị nguyên, chứng minh một bất đẳng thức. Nhưng thường thì người ta sẽ hỏi như sau: tìm x để P có giá trị nào đó (như ví dụ nêu trên), cho x nhận một giá trị cụ thể để tính P.

B. CÁC BÀI TOÁN RÈN LUYỆN

Bài 1: Cho biểu thức:

a) Rút gọn P.

b) Tìm giá trị của a để P < 1

Bài 2: Cho biểu thức: Tài liệu ôn thi vào lớp 10 môn Toán

a) Rút gọn P.

b) Tìm giá trị của x để P < 0

Bài 3: Cho biểu thức: 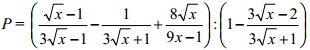Tài liệu ôn thi vào lớp 10 môn Toán

a) Rút gọn P.

b) Tìm các giá trị của x để P = 6/5.

VẤN ĐỀ 2. PHƯƠNG TRÌNH BẬC HAI MỘT ẨN

A. PHƯƠNG PHÁP GIẢI TOÁN

* Xét phương trình ax² + bx + c = 0 với a ≠ 0, biệt thức Δ = b² - 4ac

Hệ thức Viet đối với phương trình bậc hai

- Nếu ac < 0 thì PT có 2 nghiệm phân biệt.

- PT có nghiệm ↔ Δ ≥ 0.

- PT có nghiệm kép ↔ Δ = 0

- PT có 2 nghiệm phân biệt ↔ Δ > 0

Tài liệu ôn thi vào lớp 10 môn Toán

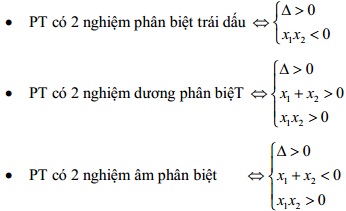
* Từ những tính chất quan trọng nêu trên, ta sẽ giải được một dạng toán về PT trùng phương.

Xét phương trình: ax⁴ + bx² + c = 0 (i) với a khác 0. Đặt t = x² ≥ 0, ta có at² + bt + c = 0 (ii)

PT (i) có 4 nghiệm phân biệt khi và chỉ khi (ii) có 2 nghiệm dương phân biệt.
PT (i) có 3 nghiệm phân biệt khi và chỉ khi (ii) có 1 nghiệm dương và 1 nghiệm bằng 0.
PT (i) có 2 nghiệm phân biệt khi và chỉ khi (ii) có duy nhất một nghiệm dương.
PT (i) có 1 nghiệm khi và chỉ khi (ii) có duy nhất một nghiệm là 0.

Sau đây chúng ta sẽ xét một số bài toán thường gặp mang tính chất điển hình.

NHỮNG ĐIỂM CẦN LƯU Ý KHI GIẢI TOÁN

- Đối với những bài toán có liên quan đến hệ thức Viet, thì ta đặc biệt quan tâm đến điều kiện để phương trình có nghiệm, tìm ra được x, ta phải đối chiếu điều kiện để PT có nghiệm.

- Ngoài các câu hỏi như trên ta còn có thể hỏi: tìm m thông qua giải bất phương trình, tìm giá trị lớn nhất nhỏ nhất.

- Đối với bài toán mà hệ số của x²không chứa tham số thì ta có thể hỏi min, max thông qua hệ thức Viet.

Chẳng hạn cho phương trình x² - 2(m+1)x + m² - 1 = 0. Tìm m để phương trình có 2 nghiệm x₁, x₂. Khi đó tìm min của biểu thức P = x₁.x₂ + 2(x₁+x₂) ta có thể làm như sau:

Dễ dàng tìm được ĐK để PT có 2 nghiệm x₁, x₂ là m ≥ -1 (các em làm đúng kĩ năng như VD). Áp dụng Vi-et ta có x₁ + x₂ = 2m + 2, x₁.x₂ = m²- 1
Khi đó ta có P = x₁.x₂ + 2(x₁ + x₂) = m² -1 + 2(2m+2) = m² + 4m + 3.
Đến đây có một sai lầm mà đa số HS mắc phải là phân tích m² + 4m + 3 = (m+2)²-1 ≥ -1. Và kết luận ngay min P = -1.

Đối với bài toán này, cách làm trên hoàn toàn sai. Dựa vào điều kiện PT có nghiệm là m ≥ -1, ta sẽ tìm min của P sao cho dấu bằng xảy ra khi m = -1. Ta có P = m² + 4m +3 = (m+1)(m+3).

Với m ≥ -1 suy ra m+1 ≥ 0, m+3 > 0 suy ra (m+1)(m+3) ≥ 0.

Vậy min P = 0, dấu bằng xảy ra khi m = -1 (thỏa mãn ĐK đã nêu).

Tài liệu ôn thi vào lớp 10 môn Toán được VnDoc chia sẻ trên đây, giúp các bạn học sinh có thêm tài liệu ôn tập chuẩn bị tốt cho kì thi sắp tới. Chúc các bạn học tốt, đồng thời các bạn đừng quên tham khảo thêm nhiều tài liệu chất lượng và bổ ích tại VnDoc.com nhé

............................................

Ngoài Tài liệu ôn thi vào lớp 10 môn Toán. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2020 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt