VnDoc.com

Đề thi tuyển sinh lớp 10 môn Toán năm 2020 số 3

Đề ôn thi vào lớp 10 môn Toán có đáp án

Thư viện Đề thi - Trắc nghiệm - Tài liệu học tập miễn phí

Trang chủ: https://vndoc.com/ | Email hỗ trợ: hotro@vndoc.com | Hotline: 024 2242 6188

Đề thi tuyển sinh lớp 10 môn Toán số 3

A. Đề ôn thi vào lớp 10 môn Toán số 3

Bài 1: Cho biểu thức

2

2 1 1 2 2

1

x x x x x

P

x x x x x x x x

   

  

   

với

0; 1xx

a, Rút gọn biểu thức

P

b, Tìm các giá trị

x

để

P

nhận giá trị nguyên

Bài 2:

1. Cho phương trình

22

2 6 0x mx m m    

(

m

là tham số). Tìm giá trị của

m

để phương trình có hai nghiệm

12

;xx

sao cho

12

8xx

2. Giải hệ phương trình:

11

2

11

34

1

11

xy















  







Bài 3: Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:

Hai ô tô cùng khởi hành một lúc từ 2 tỉnh A và B cách nhau 400km đi ngược chiều và

gặp nhau sau 5h. Nếu vận tốc của mỗi xe không thay đổi nhưng xe đi chậm xuất

phát trước xe kia 40 phút thì 2 xe gặp nhau sau 5h 22 phút kể từ lúc xe chậm khởi

hành. Tính vận tốc mỗi xe.

Bài 4: Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O;R). Giả sửa các đểm

B, C cố định và A di động trên đường tròn (O) sao cho AB < AC và AC < BC. ĐƯờng

trung trực của đoạn thẳng AB cắt AC và BC lần lượt tại P và Q. Đường trung trực

của đoạn thẳng AC cắt AB và BC lần lượt tại M và N.

1. Chứng minh rằng: OM.OM = R

2

2. Chứng minh rằng bốn điểm M, N, P, Q cùng nằm trên một đường tròn

3. Giả sử hai đường tròn ngoại tiếp tam giác BMN và CPQ cắt nhau tại S và T.

Chứng minh ba điểm S, T, O thẳng hàng

Bài 5:

Thư viện Đề thi - Trắc nghiệm - Tài liệu học tập miễn phí

Trang chủ: https://vndoc.com/ | Email hỗ trợ: hotro@vndoc.com | Hotline: 024 2242 6188

Cho các số thực x, y,z là các số thực dương thỏa mãn: xyz = 1. Tìm giá trị lớn nhất

của biểu thức:

3 3 3 3 3 3

1 1 1

A

1 1 1x y y z z x

  

     

--------------------------------------------------

Thư viện Đề thi - Trắc nghiệm - Tài liệu học tập miễn phí

Trang chủ: https://vndoc.com/ | Email hỗ trợ: hotro@vndoc.com | Hotline: 024 2242 6188

B. Đáp án đề ôn thi vào lớp 10 môn Toán số 3

Bài 1:

1, Rút gọn biểu thức

P

Với điều kiện

0; 1xx

, ta có:

       

    

  

 

  

2 1 2 2 1

1 1 1 1 1

2 1 1 2 2 1

11

2

11

12

11

2

1

x x x x x

P

x x x x x x x x x x

x x x x x x x

x x x x

x x x

x x x x

xx

x x x

x

xx

   

  

       

      



  





  





  







2, Tìm các giá trị

x

để

P

nhận giá trị nguyên

Với điều kiện

0; 1 1 1 1x x x x x       

2 2 1

0 1 2

1 1 1

xx

P

x x x x



      

   

Do

P

nguyên suy ra

2

1 1 1

1

x

Px

xx



    



(loại)

Vậy không có giá trị nào của

P

để

P

nhận giá trị nguyên

Lưu ý: Cách làm lấy mẫu số là ước của tử số không áp dụng được với bài toán này.

Bởi đề bài yêu cầu tìm các giá trị của

x

để

P

nhận giá trị nguyên,

x

nên

Đề thi thử vào lớp 10 môn Toán (Có đáp án)

Đề thi thử vào lớp 10 môn Toán năm học 2020 - 2021 do thư viện đề thi VnDoc sưu tầm và chỉnh lý. Đây là đề thi thử môn Toán lớp 10 dành cho các bạn học sinh ôn tập, củng cố kiến thức luyện thi vào lớp 10. Mời các bạn tham khảo các đề thi dưới đây

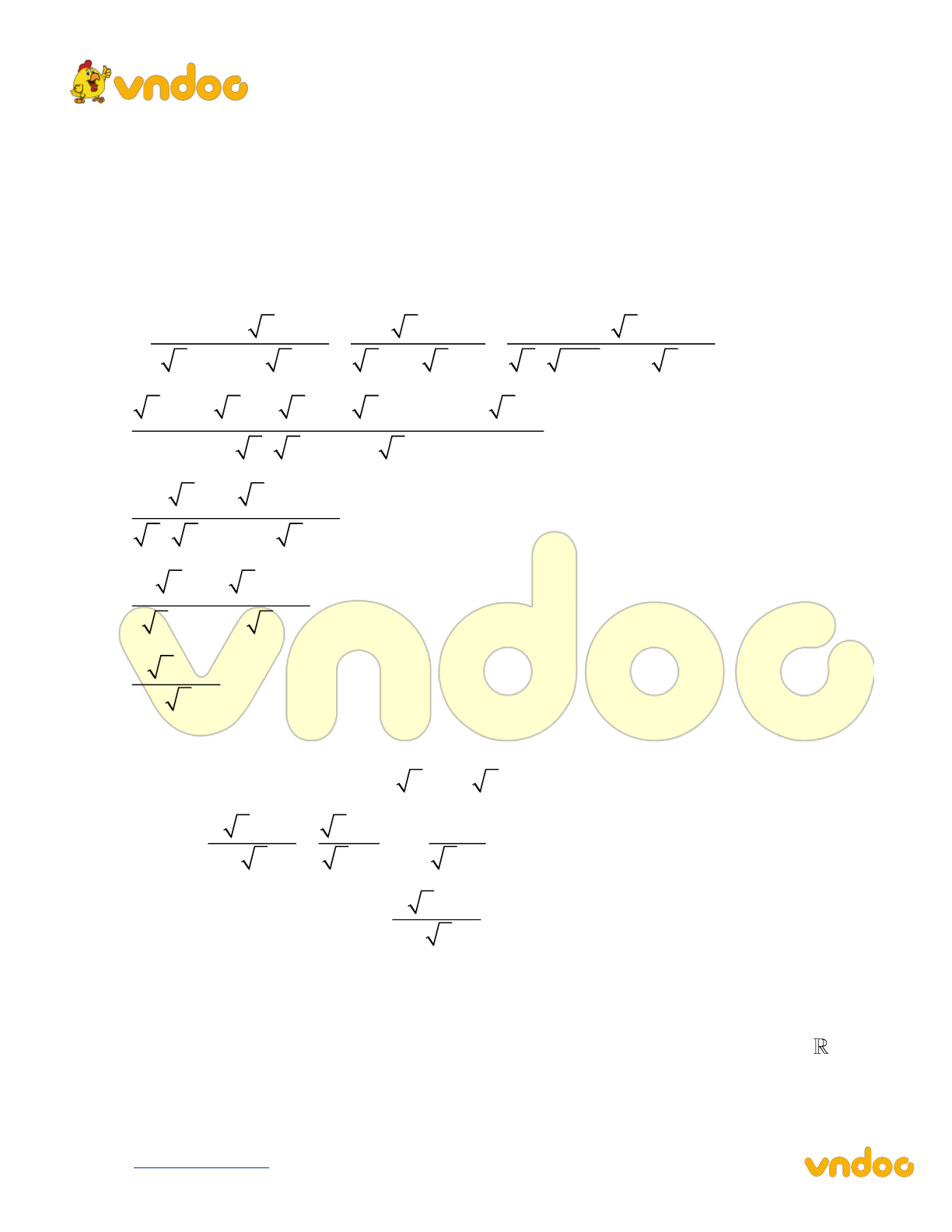
Đây là đề thi thử vào lớp 10 môn Toán được biên tập theo cấu trúc giống với đề thi tuyển sinh vào lớp 10 môn Toán của Bộ Giáo dục và Đào tạo, bao gồm 5 bài từ cơ bản tới nâng cao, tóm tắt toàn bộ kiến thức đã được học trong chương trình Toán lớp 9 kèm với hướng dẫn giải đáp. Qua đó sẽ giúp các bạn học sinh củng cố và ôn tập để chuẩn bị cho kì thi vào lớp 10 sắp tới.

-----------

Ngoài đề thi thử vào lớp 10 môn Toán này, mời các bạn học sinh tham khảo thêm các đề thi vào 10 các môn Toán, Văn, Anh,...cũng như thông tin tuyển sinh và điểm thi vào lớp 10 mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu này sẽ giúp các bạn rèn luyện thêm kỹ năng giải đề Toán lớp 9 ôn thi vào lớp 10 và làm bài tốt hơn. Chúc các bạn học tập tốt!

Xem thêm đề thi vào lớp 10 các môn Toán, Văn, Tiếng Anh:

Môn Toán	Môn Văn	Môn Tiếng Anh
Tải đề thi vào lớp 10 môn Toán	Tải đề thi vào lớp 10 môn Văn	Tải đề thi vào lớp 10 môn Tiếng Anh