Chứng minh 3 điểm thẳng hàng trong đường tròn
Chuyên đề thi vào lớp 10: Chứng minh 3 điểm thẳng hàng
Trong chương đường tròn Toán lớp 9, dạng toán chứng minh 3 điểm thẳng hàng là nội dung quan trọng, thường xuất hiện trong các bài kiểm tra và đề luyện thi vào lớp 10. Dạng bài này yêu cầu học sinh phải kết hợp linh hoạt các kiến thức về góc, tiếp tuyến, dây cung và tính chất hình học.
Bài viết này sẽ hệ thống cách chứng minh 3 điểm thẳng hàng trong đường tròn theo hướng logic, dễ hiểu, giúp học sinh nắm chắc phương pháp và vận dụng hiệu quả khi làm bài.
I. Cách chứng minh ba điểm thẳng hàng
+ Chứng minh một điểm thuộc đường thẳng chứa hai điểm còn lại
+ Chứng minh qua 3 điểm xác định được một góc bẹt
+ Chứng minh hai góc ở vị trí đối đỉnh mà bằng nhau
+ Chứng minh 3 điểm xác định được hai đường thẳng cùng vuông góc hay cùng song song với một đường thẳng thứ ba
+ Dùng tính chất đường trung trực
+ Dùng tính chất tia phân giác
+ Sử dụng tính chấy đồng quy của các đường: trung tuyến, phân giác, đường cao trong tam giác
+ Sử dụng tính chất đường chéo của các tứ giác đặc biệt
+ Sử dụng tính chất tâm và đường kính của đường tròn
+ Sử dụng tính chất hai đường tròn tiếp xúc nhau
II. Bài tập ví dụ cho bài toán chứng minh ba điểm thẳng hàng trong đường tròn
Bài 1: Cho đường tròn (O), đường kính AB. Lấy điểm C nằm giữa O và B, lấy điểm D trên đường tròn (O) sao cho AD = BC. Kẻ CH vuông góc với AD (H thuộc AD). Tia phân giác của góc DAB cắt đường tròn (O) tại điểm thứ hai E và cắt CH tại F. DF cắt đường tròn (O) tại điểm thứ hai N
a, Chứng minh CH // BD
b, Chứng minh tứ giác AFCN nội tiếp
c, Chứng minh ba điểm N, C, E thẳng hàng
Hướng dẫn giải
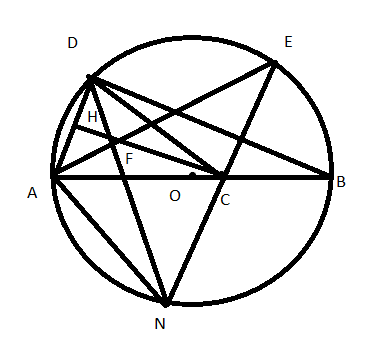
a, + Có ![]() \(\widehat {ADB}\) nhìn đường kính AB nên suy ra AD vuông góc với DB
\(\widehat {ADB}\) nhìn đường kính AB nên suy ra AD vuông góc với DB
+ Có CH vuông góc với AD (giả thiết)
Suy ra CH song song với BD (từ vuông góc đến song song)
b, + CH // BD suy ra ![]() \(\widehat {HCA} = \widehat {DBA}\) (đồng vị)
\(\widehat {HCA} = \widehat {DBA}\) (đồng vị)
lại có ![]() \(\widehat {AND} = \widehat {ABD}\) (cùng chắn cung AD)
\(\widehat {AND} = \widehat {ABD}\) (cùng chắn cung AD)
Suy ra ![]() \(\widehat {AND} = \widehat {HCA}\left( { = \widehat {ABD}} \right)\)
\(\widehat {AND} = \widehat {HCA}\left( { = \widehat {ABD}} \right)\)
+ Tứ giác AECN có:
![]() \(\widehat {AND} = \widehat {HCA}\)
\(\widehat {AND} = \widehat {HCA}\)
Hai góc cùng nhìn một cạnh
Suy ra 4 điểm A, E, N, C thuộc một đường tròn hay tứ giác AECN nội tiếp
c, + Tứ giác AFCN nội tiếp đường tròn có ![]() \(\widehat {NAF} + \widehat {NCF} = {180^0}\) (3) và
\(\widehat {NAF} + \widehat {NCF} = {180^0}\) (3) và ![]() \(\widehat {AFC} + \widehat {ANC} = {180^0}\)(4)
\(\widehat {AFC} + \widehat {ANC} = {180^0}\)(4)
Ta có ![]() \(\widehat {AFC} + \widehat {CFE} = {180^0}\)(5) (2 góc kề bù)
\(\widehat {AFC} + \widehat {CFE} = {180^0}\)(5) (2 góc kề bù)
+ Từ (4) và (5) suy ra ![]() \(\widehat {ANC} = \widehat {CFE}\)
\(\widehat {ANC} = \widehat {CFE}\)
+ Xét tam giác NAE và tam giác FCE có
Góc ![]() \(\widehat {CEF}\) chung
\(\widehat {CEF}\) chung
![]() \(\widehat {ANC} = \widehat {CFE}\)
\(\widehat {ANC} = \widehat {CFE}\)
Suy ra hai tam giác NAE đồng dạng với tam giác FCE
Suy ra hai góc ![]() \(\widehat {FCE} = \widehat {NAF}\)(2 góc tương ứng bằng nhau) (3)
\(\widehat {FCE} = \widehat {NAF}\)(2 góc tương ứng bằng nhau) (3)
Từ (3) và (6) suy ra ![]() \(\widehat {NCF} + \widehat {FCE} = {180^0}\)
\(\widehat {NCF} + \widehat {FCE} = {180^0}\)
Suy ra N, C, E thẳng hàng
Bài 2: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Đường thẳng AO cắt (O) tại E và đường thẳng AO’ cắt (O’) tại F. Chứng minh rằng E, B, F thẳng hàng.
Hướng dẫn giải
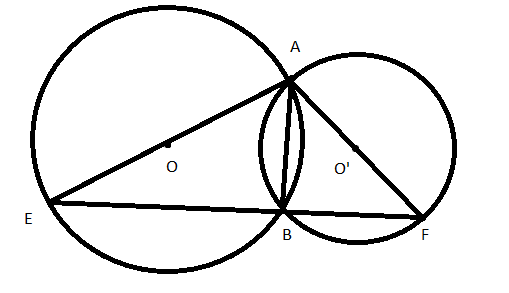
+ Có ![]() \(\widehat {ABE}\) nhìn đường kính AE nên
\(\widehat {ABE}\) nhìn đường kính AE nên ![]() \(\widehat {ABE} = {90^0}\)
\(\widehat {ABE} = {90^0}\)
+ Có ![]() \(\widehat {ABF}\) nhìn đường kính AF nên
\(\widehat {ABF}\) nhìn đường kính AF nên ![]() \(\widehat {ABF} = {90^0}\)
\(\widehat {ABF} = {90^0}\)
+ Có ![]() \(\widehat {ABE} + \widehat {ABF} = {90^0} + {90^0} = {180^0}\)
\(\widehat {ABE} + \widehat {ABF} = {90^0} + {90^0} = {180^0}\)
Suy ra 3 điểm E, B, F thẳng hàng
Bài 3: Cho đường tròn tâm O đường kính AB = 2R. Gọi M là một điểm bất kì thuộc đường tròn (O) khác A và B. Các tiếp tuyến của O tại A và M cắt nhau tại E. Vẽ MP vuông góc với AB (P thuộc AB), vẽ MQ vuông góc với AE (Q thuộc AE)
a, Chứng minh AEMO là tứ giác nội tiếp đường tròn và APMQ là hình chữ nhật.
b, Gọi I là trung điểm của PQ. Chứng minh O, I, E thẳng hàng
Hướng dẫn giải

a, Chứng minh AEMO là tứ giác nội tiếp đường tròn và APMQ là hình chữ nhật.
+ Có AE là tiếp tuyến của đường tròn O ![]() \(\Rightarrow \widehat {OAE}= 90^0\)
\(\Rightarrow \widehat {OAE}= 90^0\)
Có EM là tiếp tuyến của đường tròn O ![]() \(\Rightarrow \widehat {EMO}= 90^0\)
\(\Rightarrow \widehat {EMO}= 90^0\)
+ Xét tứ giác AEMO có:
![]() \(\widehat {OAE} + \widehat {OME} = {90^0} + {90^0} = {180^0}\)
\(\widehat {OAE} + \widehat {OME} = {90^0} + {90^0} = {180^0}\)
mà hai góc ở vị trí đối nhau
Suy ra tứ giác AEMO là tứ giác nội tiếp đường tròn.
+ Xét tứ giác APMQ có:
![]() \(\widehat {PAQ} = \widehat {AQM} = \widehat {MPA} = {90^0}\)
\(\widehat {PAQ} = \widehat {AQM} = \widehat {MPA} = {90^0}\)
Suy ra tứ giác APMQ là hình chữ nhật (dhnb)
b, Chứng minh O, I, E thẳng hàng
+ Nối A với M và E với O
+ Có AE và ME là hai tiếp tuyến cắt nhau tại E nên EO đi qua trung điểm AM (1)
+ Có APMQ là hình chữ nhật, suy ra AM và PQ cắt nhau tại trung điểm I của mỗi đường (tính chất) (2)
+ Từ (1) và (2) suy ra ba điểm E, I, O thẳng hàng.
Bài 4: Cho tam giác ![]() \(ABC\) có ba góc nhọn nội tiếp đường tròn
\(ABC\) có ba góc nhọn nội tiếp đường tròn ![]() \((O)\) với trực tâm
\((O)\) với trực tâm ![]() \(H\). Giả sử
\(H\). Giả sử ![]() \(M\) là một điểm trên cung
\(M\) là một điểm trên cung ![]() \(BC\) không chứa
\(BC\) không chứa ![]() \(A\) (với
\(A\) (với ![]() \(M \neq
B;N \neq C\)). Gọi
\(M \neq
B;N \neq C\)). Gọi ![]() \(N;P\) theo thứ tự là điểm đối xứng của
\(N;P\) theo thứ tự là điểm đối xứng của ![]() \(M\) qua các đường thẳng
\(M\) qua các đường thẳng ![]() \(AB;AC\).
\(AB;AC\).
a) Chứng minh ![]() \(AHCP\) là tứ giác nội tiếp.
\(AHCP\) là tứ giác nội tiếp.
b) Chứng minh ![]() \(N;H;P\) thẳng hàng.
\(N;H;P\) thẳng hàng.
c) Tìm vị trí của điểm ![]() \(M\) để độ dài đoạn thẳng
\(M\) để độ dài đoạn thẳng ![]() \(NP\) lớn nhất.
\(NP\) lớn nhất.
Hướng dẫn giải
Hình vẽ minh họa
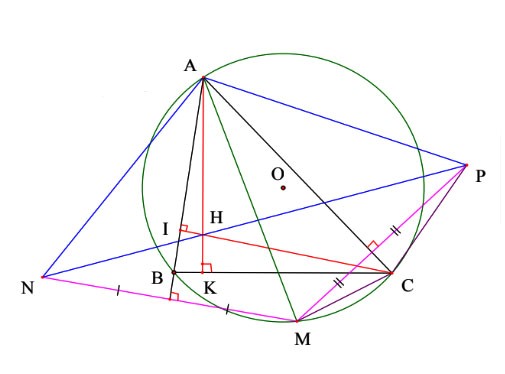
a) Gọi ![]() \(I = CH \cap AB;K = AH \cap
BC\)
\(I = CH \cap AB;K = AH \cap
BC\)
Ta có: ![]() \(\widehat{IBK} =
\widehat{AMC}\) (cùng chắn cung
\(\widehat{IBK} =
\widehat{AMC}\) (cùng chắn cung ![]() \(AC\))
\(AC\))
![]() \(\widehat{AMC} = \widehat{APC}\) (do
\(\widehat{AMC} = \widehat{APC}\) (do ![]() \(P\) đối xứng với
\(P\) đối xứng với ![]() \(M\) qua
\(M\) qua ![]() \(AC\))
\(AC\))
![]() \(\Rightarrow \widehat{IBK} =
\widehat{APC}(*)\)
\(\Rightarrow \widehat{IBK} =
\widehat{APC}(*)\)
Ta thấy ![]() \(BIHK\) nội tiếp nên
\(BIHK\) nội tiếp nên ![]() \(\widehat{IBK} + \widehat{AHC} =
180^{0}(**)\)
\(\widehat{IBK} + \widehat{AHC} =
180^{0}(**)\)
Từ (*) và (**) suy ra ![]() \(\widehat{AHC} +
\widehat{APC} = 180^{0}\)
\(\widehat{AHC} +
\widehat{APC} = 180^{0}\)
Vậy ![]() \(AHCP\) là tứ giác nội tiếp.
\(AHCP\) là tứ giác nội tiếp.
b) Do tứ giác ![]() \(AHCP\) là tứ giác nội tiếp đường tròn nên
\(AHCP\) là tứ giác nội tiếp đường tròn nên ![]() \(\widehat{AHP} =
\widehat{ACP}\) (cùng chắn cung
\(\widehat{AHP} =
\widehat{ACP}\) (cùng chắn cung ![]() \(AP\))
\(AP\))
Mà ![]() \(\widehat{ACP} =
\widehat{ACM}\)(tính chất đối xứng)
\(\widehat{ACP} =
\widehat{ACM}\)(tính chất đối xứng) ![]() \(\Rightarrow \widehat{AHP} =
\widehat{ACM}(1)\)
\(\Rightarrow \widehat{AHP} =
\widehat{ACM}(1)\)
Tương tự ta chứng minh được tứ giác ![]() \(AHBN\) nội tiếp nên
\(AHBN\) nội tiếp nên ![]() \(\widehat{AHN} = \widehat{ABN}\)(cùng chắn cung
\(\widehat{AHN} = \widehat{ABN}\)(cùng chắn cung ![]() \(AP\))
\(AP\))
Suy ra ![]() \(\widehat{AHN} =
\widehat{ABM}(2)\)
\(\widehat{AHN} =
\widehat{ABM}(2)\)
Vì tứ giác ![]() \(ABMC\) nội tiếp nên
\(ABMC\) nội tiếp nên ![]() \(\widehat{ACM} + \widehat{ABM} =
180^{0}(3)\)
\(\widehat{ACM} + \widehat{ABM} =
180^{0}(3)\)
Từ (1); (2); (3) suy ra ![]() \(\widehat{AHP} =
\widehat{AHN} = 180^{0}\)
\(\widehat{AHP} =
\widehat{AHN} = 180^{0}\)
Vậy ![]() \(N;H;P\) thẳng hàng.
\(N;H;P\) thẳng hàng.
c) Từ  \(\left\{ \begin{matrix}
\widehat{MAN} = 2\widehat{BAM} \\
\widehat{MAP} = 2\widehat{MAC} \\
\end{matrix} \right.\)
\(\left\{ \begin{matrix}
\widehat{MAN} = 2\widehat{BAM} \\
\widehat{MAP} = 2\widehat{MAC} \\
\end{matrix} \right.\)
![]() \(\Rightarrow \widehat{NAP} = 2\left(
\widehat{BAM} + \widehat{MAC} \right) = 2\widehat{BAC}\) không đổi
\(\Rightarrow \widehat{NAP} = 2\left(
\widehat{BAM} + \widehat{MAC} \right) = 2\widehat{BAC}\) không đổi
Ta có: ![]() \(NP = 2AP.\sin\widehat{BAC} =2AM.\sin\widehat{BAC}\)
\(NP = 2AP.\sin\widehat{BAC} =2AM.\sin\widehat{BAC}\)
Do đó ![]() \(NP\) lớn nhất khi và chỉ khi
\(NP\) lớn nhất khi và chỉ khi ![]() \(AM\) lớn nhất. Khi đó
\(AM\) lớn nhất. Khi đó ![]() \(AM\) là đường kính đường tròn
\(AM\) là đường kính đường tròn ![]() \((O)\).
\((O)\).
Vậy ![]() \(NP\) lớn nhất khi và chỉ khi
\(NP\) lớn nhất khi và chỉ khi ![]() \(M\) là điểm đối xứng của
\(M\) là điểm đối xứng của ![]() \(A\) qua
\(A\) qua ![]() \(O\).
\(O\).
Bài 5: Cho hai đường tròn ![]() \((O)\) và
\((O)\) và  \((O')\) cắt nhau tại
\((O')\) cắt nhau tại ![]() \(A\) và
\(A\) và ![]() \(B\). Vẽ
\(B\). Vẽ ![]() \(AC;AD\) theo thứ tự là đường kính của hai đường tròn
\(AC;AD\) theo thứ tự là đường kính của hai đường tròn ![]() \((O)\) và
\((O)\) và  \((O')\).
\((O')\).
a) Chứng minh ba điểm ![]() \(C;B;D\) thẳng hàng.
\(C;B;D\) thẳng hàng.
b) Đường thẳng ![]() \(AC\) cắt đường tròn
\(AC\) cắt đường tròn  \((O')\) tại
\((O')\) tại ![]() \(E\), đường thẳng
\(E\), đường thẳng ![]() \(AD\) cắt đường tròn
\(AD\) cắt đường tròn ![]() \((O)\) tại
\((O)\) tại ![]() \(F\) (với
\(F\) (với ![]() \(E;F
\neq A\)). Chứng minh bốn điểm
\(E;F
\neq A\)). Chứng minh bốn điểm ![]() \(C;D;E;F\) cùng nằm trên một đường tròn.
\(C;D;E;F\) cùng nằm trên một đường tròn.
Hướng dẫn giải
Hình vẽ minh họa
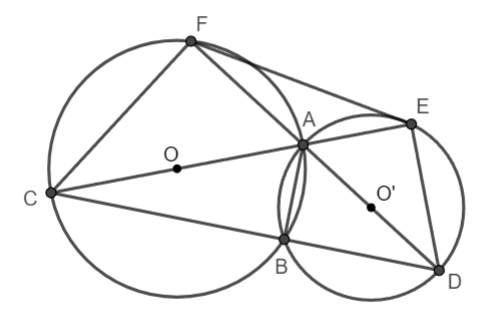
a) Ta có: ![]() \(\widehat{ABC};\widehat{ABD}\) lần lượt là các góc nội tiếp chắn nửa đường tròn
\(\widehat{ABC};\widehat{ABD}\) lần lượt là các góc nội tiếp chắn nửa đường tròn  \((O);(O')\)
\((O);(O')\)
![]() \(\Rightarrow \widehat{ABC} =
\widehat{ABD} = 90^{0}\)
\(\Rightarrow \widehat{ABC} =
\widehat{ABD} = 90^{0}\)
![]() \(\Rightarrow \widehat{ABC} +
\widehat{ABD} = 180^{0}\)
\(\Rightarrow \widehat{ABC} +
\widehat{ABD} = 180^{0}\)
Vậy ba điểm ![]() \(C;B;D\) thẳng hàng.
\(C;B;D\) thẳng hàng.
b) Xét tứ giác CDEF ta có:
![]() \(\widehat{CFD} = \widehat{CFA} =
90^{0}\)(góc nội tiếp chắn nửa đường tròn (O))
\(\widehat{CFD} = \widehat{CFA} =
90^{0}\)(góc nội tiếp chắn nửa đường tròn (O))
![]() \(\widehat{CED} = \widehat{DEA} =
90^{0}\)(góc nội tiếp chắn nửa đường tròn (O’))
\(\widehat{CED} = \widehat{DEA} =
90^{0}\)(góc nội tiếp chắn nửa đường tròn (O’))
![]() \(\Rightarrow \widehat{CFD} = \widehat{CED}
= 90^{0}\) suy ra CDEF là tứ giác nội tiếp.
\(\Rightarrow \widehat{CFD} = \widehat{CED}
= 90^{0}\) suy ra CDEF là tứ giác nội tiếp.
Bài 6: Cho tam giác nhọn ABC , Kẻ các đường cao AD, BE, CF. Gọi H là trực tâm của tam giác. Gọi M, N, P, Q lần lượt là các hình chiếu vuông góc của D lên AB, BE, CF, AC. Chứng minh :
1. Các tứ giác DMFP, DNEQ là hình chữ nhật.
2. Các tứ giác BMND; DNHP; DPQC nội tiếp .
3. Hai tam giác HNP và HCB đồng dạng.
4. Bốn điểm M, N, P, Q thẳng hàng.
Hướng dẫn giải
Hình vẽ minh họa
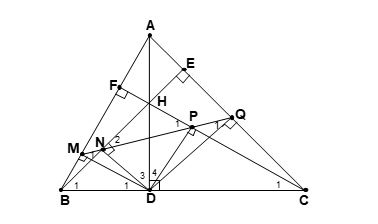
1. & 2. (HS tự làm)
3. Theo chứng minh trên DNHP nội tiếp => ∠N2 = ∠D4 (nội tiếp cùng chắn cung HP); ∆HDC có ∠HDC = 900 (do AH là đường cao) ∆ HDP có ∠HPD = 900 (do DP ⊥ HC) => ∠C1= ∠D4 (cùng phụ với ∠DHC)=> ∠C1=∠N2 (1) chứng minh tương tự ta có ∠B1=∠P1 (2)
Từ (1) và (2) => ∆HNP ∼ ∆ HCB
4. Theo chứng minh trên DNMB nội tiếp => ∠N1 = ∠D1 (nội tiếp cùng chắn cung BM).(3)
DM // CF ( cùng vuông góc với AB) => ∠C1= ∠D1 ( hai góc đồng vị).(4)
Theo chứng minh trên ∠C1 = ∠N2 (5)
Từ (3), (4), (5) => ∠N1 = ∠N2 mà B, N, H thẳng hàng => M, N, P thẳng hàng. (6)
Chứng minh tương tự ta cung có N, P, Q thẳng hàng . (7)
Từ (6), (7) => Bốn điểm M, N, P, Q thẳng hàng
Bài 7: AB và AC là hai tiếp tuyến của đường tròn tâm O bán kính R (B, C là tiếp điểm). Vẽ CH vuông góc AB tại H, cắt (O) tại E và cắt OA tại D.
1. Chứng minh CO = CD.
2. Chứng minh tứ giác OBCD là hình thoi.
3. Gọi M là trung điểm của CE, Bm cắt OH tại I. Chứng minh I là trung điểm của OH.
4. Tiếp tuyến tại E với (O) cắt AC tại K. Chứng minh ba điểm O, M, K thẳng hàng.
Hướng dẫn giải
Hình vẽ minh họa
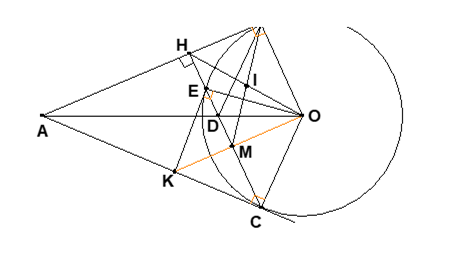
1. Theo giả thiết AB và AC là hai tiếp tuyến của đường tròn tâm O => OA là tia phân giác của ∠BOC => ∠BOA = ∠COA (1)
OB ⊥ AB ( AB là tiếp tuyến ); CH ⊥ AB (gt) => OB // CH => ∠BOA = ∠CDO (2)
Từ (1) và (2) => ∆COD cân tại C => CO = CD.(3)
2. theo trên ta có CO = CD mà CO = BO (= R) => CD = BO (4) lại có OB // CH hay OB // CD (5)
Từ (4) và (5) => BOCD là hình bình hành (6) . Từ (6) và (3) => BOCD là hình thoi.
3. M là trung điểm của CE => OM ⊥ CE ( quan hệ đường kính và dây cung) => ∠OMH = 900. theo trên ta cũng có ∠OBH =900; ∠BHM =900 => tứ giác OBHM là hình chữ nhật => I là trung điểm của OH.
4. M là trung điểm của CE; KE và KC là hai tiếp tuyến => O, M, K thẳng hàng.
Bài 8. Cho đường tròn (O) đường kính AC. Trên bán kính OC lấy điểm B tuỳ ý (B khác O, C ). Gọi M là trung điểm của đoạn AB. Qua M kẻ dây cung DE vuông góc với AB. Nối CD, Kẻ BI vuông góc với CD. Chứng minh tứ giác BMDI nội tiếp .
2. Chứng minh tứ giác ADBE là hình thoi.
3. Chứng minh BI // AD.
4. Chứng minh I, B, E thẳng hàng.
5. Chứng minh MI là tiếp tuyến của (O’).
Hướng dẫn giải
1. ∠BIC = 900 ( nội tiếp chắn nửa đường tròn ) => ∠BID = 900 (vì là hai góc kề bù); DE ⊥ AB tại M => ∠BMD = 900
=> ∠BID + ∠BMD = 1800 mà đây là hai góc đối của tứ giác MBID nên MBID là tứ giác nội tiếp.
2. Theo giả thiết M là trung điểm của AB; DE ⊥ AB tại M nên M cũng là trung điểm của DE (quan hệ đường kính và dây cung)
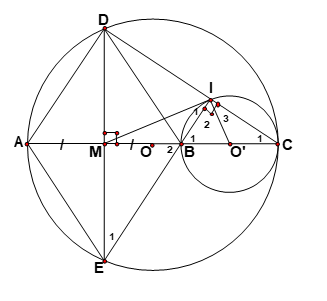
=> Tứ giác ADBE là hình thoi vì có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường .
3. ∠ADC = 900 ( nội tiếp chắn nửa đường tròn ) => AD ⊥ DC; theo trên BI ⊥ DC => BI // AD. (1)
4. Theo giả thiết ADBE là hình thoi => EB // AD (2).
Từ (1) và (2) => I, B, E thẳng hàng (vì qua B chỉ có một đường thẳng song song với AD mà thôi.)
5. I, B, E thẳng hàng nên tam giác IDE vuông tại I => IM là trung tuyến ( vì M là trung điểm của DE) =>MI = ME => ∆MIE cân tại M
=> ∠I1 = ∠E1 ; ∆O’IC cân tại O’ ( vì O’C và O’I cùng là bán kính )
=> ∠I3 = ∠C1 mà ∠C1 = ∠E1 ( Cùng phụ với góc EDC )
=> ∠I1 = ∠I3 => ∠I1 + ∠I2 = ∠I3 + ∠I2 .
Mà ∠I3 + ∠I2 = ∠BIC = 900 => ∠I1 + ∠I2 = 900 = ∠MIO’ hay MI ⊥ O’I tại I
=> MI là tiếp tuyến của (O’).
Bài 6. Cho đường tròn (O; R) và (O’; R’) có R > R’ tiếp xúc ngoài nhau tại C. Gọi AC và BC là hai đường kính đi qua điểm C của (O) và (O’). DE là dây cung của (O) vuông góc với AB tại trung điểm M của AB. Gọi giao điểm thứ hai của DC với (O’) là F, BD cắt (O’) tại G.
Chứng minh rằng:
1. Tứ giác MDGC nội tiếp .
2. Bốn điểm M, D, B, F cùng nằm trên một đường tròn
3. Tứ giác ADBE là hình thoi.
4. B, E, F thẳng hàng
5. DF, EG, AB đồng quy.
6. MF = 1/2 DE.
7. MF là tiếp tuyến của (O’).
Hướng dẫn giải:
1. ∠BGC = 900 ( nội tiếp chắn nửa đường tròn )
=> ∠CGD = 900 (vì là hai góc kề bù)
Theo giả thiết DE ⊥ AB tại M => ∠CMD = 900
=> ∠CGD + ∠CMD = 1800 mà đây là hai góc đối của tứ giác MCGD nên MCGD là tứ giác nội tiếp
2. ∠BFC = 900 ( nội tiếp chắn nửa đường tròn ) => ∠BFD = 900; ∠BMD = 900 (vì DE ⊥ AB tại M) như vậy F và M cùng nhìn BD dưới một góc bằng 900 nên F và M cùng nằm trên đường tròn đường kính BD
=> M, D, B, F cùng nằm trên một đường tròn .
3. Theo giả thiết M là trung điểm của AB; DE ⊥ AB tại M nên M cũng là trung điểm của DE (quan hệ đường kính và dây cung)
=> Tứ giác ADBE là hình thoi vì có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường .
4. ∠ADC = 900 ( nội tiếp chắn nửa đường tròn ) => AD ⊥ DF; theo trên tứ giác ADBE là hình thoi
=> BE // AD mà AD ⊥ DF nên suy ra BE ⊥ DF .
Theo trên ∠BFC = 900 ( nội tiếp chắn nửa đường tròn )
=> BF ⊥ DF mà qua B chỉ có một đường thẳng vuông góc với DF do đo B, E, F thẳng hàng.
5. Theo trên DF ⊥ BE; BM ⊥ DE mà DF và BM cắt nhau tại C nên C là trực tâm của tam giác BDE
=> EC cũng là đường cao => EC⊥BD; theo trên CG⊥BD => E,C,G thẳng hàng.
Vậy DF, EG, AB đồng quy
6. Theo trên DF ⊥ BE => ∆DEF vuông tại F có FM là trung tuyến (vì M là trung điểm của DE) suy ra
MF = 1/2 DE ( vì trong tam giác vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền).
7. (HD) theo trên MF = 1/2 DE => MD = MF
=> ∆MDF cân tại M => ∠D1 = ∠F1
∆O’BF cân tại O’ ( vì O’B và O’F cùng là bán kính)
=> ∠F3 = ∠B1 mà ∠B1 = ∠D1 (Cùng phụ với ∠DEB)
=> ∠F1 = ∠F3 => ∠F1 + ∠F2 = ∠F3 + ∠F2 . Mà ∠F3 + ∠F2 = ∠BFC = 900
=> ∠F1 + ∠F2 = 900 = ∠MFO’ hay MF ⊥ O’F tại F => MF là tiếp tuyến của (O’).
Bài 7. Cho tam giác ABC vuông ở A. Dựng ở miền ngoài tam giác ABC các hình vuông ABHK, ACDE. 1. Chứng minh ba điểm H, A, D thẳng hàng.
2. Đường thẳng HD cắt đường tròn ngoại tiếp tam giác ABC tại F, chứng minh FBC là tam giác vuông cân.
3. Cho biết ∠ABC > 450 ; gọi M là giao điểm của BF và ED. Chứng minh 5 điểm B, K, E, M, C cùng nằm trên một đường tròn.
4. Chứng minh MC là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
1. Theo giả thiết ABHK là hình vuông => ∠BAH = 450
Tứ giác AEDC là hình vuông => ∠CAD = 450; tam giác ABC vuông ở A => ∠BAC = 900
=> ∠BAH + ∠BAC + ∠CAD = 450 + 900 + 450 = 1800 => Ba điểm H, A, D thẳng hàng.
2. Ta có ∠BFC = 900 (nội tiếp chắn nửa đường tròn ) nên tam giác BFC vuông tại F. (1).
∠FBC = ∠FAC (nội tiếp cùng chắn cung FC) mà theo trên ∠CAD = 450 hay ∠FAC = 450 (2).
Từ (1) và (2) suy ra ∆FBC là tam giác vuông cân tại F.
3. Theo trên ∠BFC = 900 => ∠CFM = 900 ( vì là hai góc kề bù); ∠CDM = 900 (tính chất hình vuông).
=> ∠CFM + ∠CDM = 1800 mà đây là hai góc đối nên tứ giác CDMF nội tiếp một đường tròn suy ra ∠CDF = ∠CMF , mà ∠CDF = 450 (vì AEDC là hình vuông) => ∠CMF = 450 hay ∠CMB = 450.
Ta cũng có ∠CEB = 450 (vì AEDC là hình vuông); ∠BKC = 450 (vì ABHK là hình vuông).
Như vậy K, E, M cùng nhìn BC dưới một góc bằng 450 nên cùng nằm trên cung chứa góc 450 dựng trên BC => 5 điểm B, K, E, M, C cùng nằm trên một đường tròn.
4. ∆CBM có ∠B = 450 ; ∠M = 450 => ∠BCM =450 hay MC ⊥ BC tại C => MC là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
📄 Do dung lượng nội dung lớn, tài liệu chi tiết được cung cấp dưới dạng file tải về.
===========================
Việc nắm vững phương pháp chứng minh 3 điểm thẳng hàng trong đường tròn sẽ giúp học sinh giải quyết chính xác nhiều dạng toán hình học lớp 9. Đây là nền tảng quan trọng để làm tốt các bài toán luyện thi vào lớp 10, đồng thời rèn luyện tư duy lập luận chặt chẽ và khoa học.










