Góc nội tiếp

Chuyên đề Toán học lớp 9: Góc nội tiếp được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 9 hiệu quả hơn. Mời các bạn tham khảo.

Bài: Góc nội tiếp

1. Định nghĩa

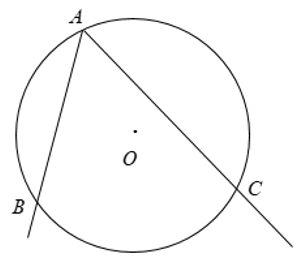
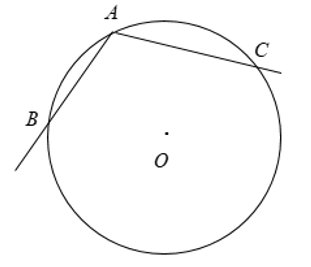
+ Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

+ Cung nằm bên trong góc được gọi là cung bị chắn.

2. Định lý.

Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.

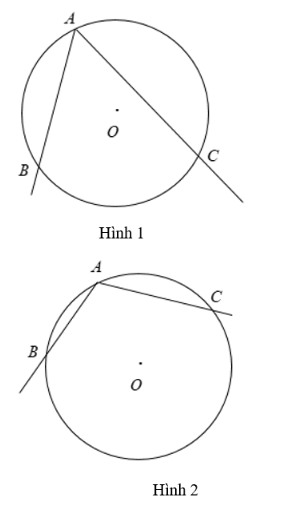
+ ∠BAC là góc nội tiếp chắn cung nhỏ BC (như hình 1) và chắn cung lớn BC (như hình 2)

+ Ta có thể viết: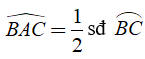

3. Hệ quả.

Trong một đường tròn:

+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

+ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

+ Góc nội tiếp (nhỏ hơn hoặc bằng 90°) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.

+ Góc nội tiếp chắn nửa đường tròn là góc vuông.

4. Ví dụ cụ thể

Câu 1: Cho tam giác ABC cân tại A (∠A = 90°). Vẽ đường tròn đường kính AB cắt BC tại D, cắt AC tại E. Chứng minh rằng: Tam giác DBE cân.

Hướng dẫn:

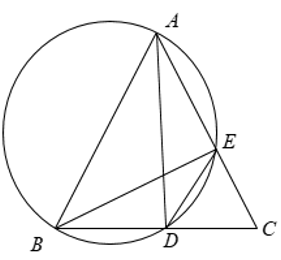
Ta có:

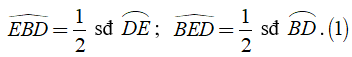
+ ∠BDA = 90° (vì ∠BDA là góc nội tiếp chắn nửa đường tròn)

⇒ AD ⊥ BC

Mà ΔABC cân tại A nên AD vừa là đường cao vừa là đường phân giác góc A.

Khi đó ta có:

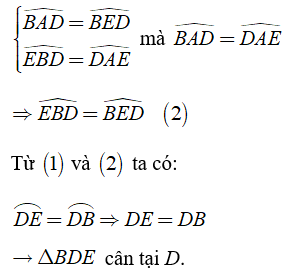
Bài lý thuyết: Góc nội tiếp trên đây các bạn học sinh cùng quý thầy cô cần nắm vững kiến thức về định nghĩa, định lý, hệ quả của góc nội tiếp...

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 9: Góc nội tiếp. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 9, Giải bài tập Toán lớp 9 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc