Bài tập áp dụng hệ thức về cạnh và góc trong tam giác vuông
Chuyên đề Toán 9: Hệ thức về cạnh và góc trong tam giác vuông
Trong chương trình Toán 9, chuyên đề tam giác vuông đóng vai trò quan trọng trong việc xây dựng nền tảng kiến thức hình học và chuẩn bị cho kỳ thi vào lớp 10. Đặc biệt, các hệ thức về cạnh và góc trong tam giác vuông không chỉ giúp học sinh rèn luyện kỹ năng tính toán chính xác mà còn là cơ sở để giải quyết nhiều dạng toán nâng cao hơn. Bài viết này sẽ hệ thống kiến thức trọng tâm, công thức quan trọng kèm theo ví dụ minh họa và bài tập vận dụng, giúp các em nắm chắc lý thuyết và tự tin trong quá trình ôn tập.
A. Bài tập áp dụng hệ thức về cạnh và góc trong tam giác vuông
Phương pháp giải:
Dùng các hệ thức về cạnh và góc trong tam giác vuông.
Bài tập 1. Cho 
\(\Delta ABC\), \(AB = 3,2cm;AC = 5,0cm\) và \(\widehat{B} = 70^{0}\). Tính độ dài \(BC\)? (Làm tròn đến hàng phần mười).
Hướng dẫn giải
Hình vẽ minh họa
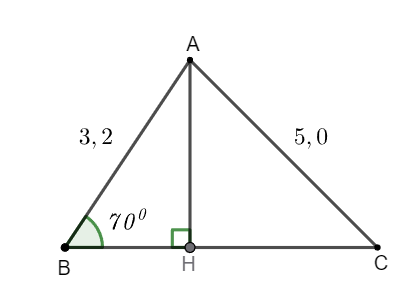
Vẽ đường cao \(AH.\) Xét \(\Delta ABH\) vuông tại \(H\) có:
\(AH = AB.\sin\ B\ = \ 3,2.\sin\ 70^{o}
\approx 3,0\) (cm).
\(BH\ = \ AB.\cos\ B\ = \ 3,2.\cos\
70^{o} \approx 1,1\) (cm).
Xét \(\Delta AHC\) vuông tại H có:
\(HC = \sqrt{AC^{2} - AH^{2}} \approx
\sqrt{5,0^{2} - 3,0^{2}} = 4,0\)(cm).
Điểm C không thể nằm giữa H và B vì trên tia HB có HC > HB. Chỉ còn trường hợp điểm H nằm giữa B và C. Ta có \(BC = BH + HC \approx 1,1 + 4,0 = 5,1\)
Bài tập 2. Cho tam giác \(\Delta ABC,\ \
AB\ = \ 14cm,\ AC\ = \ 11cm\) và\(\widehat{B}\ = 40^{0}\). Tính độ dài \(BC\)? (làm tròn đến hàng phần mười).
Hướng dẫn giải
* Phương pháp giải
Vẽ đường cao AH để vận dụng các hệ thức về cạnh và góc trong tam giác vuông. Tính HB và HC từ đó tính được BC.
* Trình bày lời giải
Hình vẽ minh họa
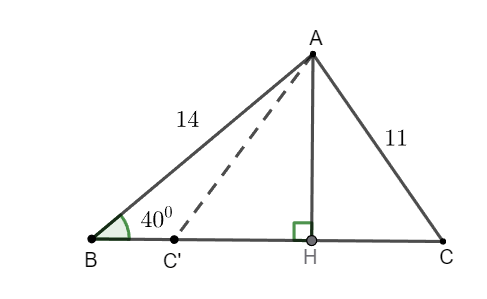
Vẽ đường cao AH. Xét ∆ABH vuông tại H có:
\(AH\ = \ AB.\sin\ B\ = \ 14.\sin\ 40^{o}
\approx 9,0\) (cm).
\(BH = AB.\cos\ B = 14.\cos\ 40^{o} \approx
10,7\) (cm).
Xét ∆AHC vuông tại H có: \(HC =
\sqrt{AC^{2} - AH^{2}} = \sqrt{11^{2} - 9^{2}} \approx
6,3\)(cm).
• Nếu H nằm giữa B và C thì \(BC = BH + HC
\approx 10,7 + 6,3 = 17\) (cm).
• Nếu C' nằm giữa B và H thì \(BC' = BH
- HC' \approx 10,7 - 6,3 = 4,4\) (cm).
C. Bài tập tự rèn luyện có hướng dẫn đáp án chi tiết
Bài tập 1: Cho tam giác \(ABC\) vuông ở A, có \(AC = 15cm,B = 50^{0}.\) Hãy tính độ dài:
a) \(AB,BC\).
b) Phân giác \(CD.\)
Bài tập 2: Không dùng máy tính và bảng số hãy chứng minh rằng:\(\sin75^{0} = \frac{\sqrt{6} +\sqrt{2}}{4}\).
Bài tập 3. Cho hình bình hành \(ABCD\) có đường chéo \(AC\) lớn hơn đường chéo \(BD.\) Kẻ \(CH\bot
AD\) \(,CK\bot AB\)
a) Chứng minh \(\Delta CKH\sim\Delta
BCA\).
b) Chứng minh \(HK =
AC.sinBAD\).
c) Tính diện tích tứ giác \(AKCH\) biết \(\widehat{BAD} = 60^{0},AB =
4cm\) và
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
-------------------------------------------------------------
Có thể thấy, việc nắm vững các hệ thức về cạnh và góc trong tam giác vuông không chỉ giúp học sinh giải quyết nhanh các bài toán trong chương trình Toán 9 mà còn tạo nền tảng quan trọng cho môn Toán ở bậc THPT. Để học tốt chuyên đề này, các em nên:
-
Học thuộc các công thức cơ bản và hiểu ý nghĩa của chúng.
-
Luyện tập nhiều dạng bài tập từ cơ bản đến nâng cao.
-
Kết hợp với việc rút kinh nghiệm từ sai lầm để củng cố kiến thức.
Thông qua quá trình ôn luyện kiên trì, học sinh sẽ tự tin hơn khi làm bài kiểm tra, bài thi và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10. Đây là bước đệm quan trọng để chinh phục những kiến thức toán học khó hơn ở bậc học tiếp theo.
