Vị trí tương đối của đường thẳng và đường tròn
Chuyên đề Toán học lớp 9: Vị trí tương đối của đường thẳng và đường tròn được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 9 hiệu quả hơn. Mời các bạn tham khảo.
Bài: Vị trí tương đối của đường thẳng và đường tròn
1. Ba vị trí tương đối của đường thẳng và đường tròn
a) Đường thẳng và đường tròn cắt nhau
Khi một đường thẳng có hai điểm chung A, B với đường tròn (O) ta nói đường thẳng cắt đường tròn tại hai điểm phân biệt. Khi đó ta có những kết quả quan trọng sau:
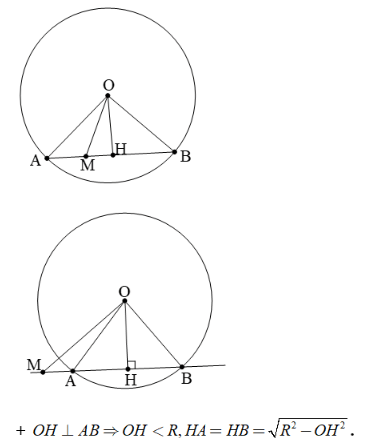
Theo định lý Pitago ta có: OH2 = MO2 - MH2
Mặt khác ta cũng có: OH2 = R2 - AH2 nên suy ra
MO2 - MH2 = R2 - AH2 ⇔ MH2 - AH2 = MO2 - R2
⇔ (MH - AH)(MH + AH) = MO2 - R2
+ Nếu M nằm ngoài đoạn AB thì MA.MB = MO2 - R2
+ Nếu M nằm trong đoạn AB thì MA.MB = R2 - MO2
Mối liên hệ khoảng cách và dây cung: R2 = OH2 + AB2/4
b) Đường thẳng và đường tròn tiếp xúc nhau.
Khi một đường thẳng Δ chỉ có một điểm chung H với đường tròn (O), ta nói đường thẳng tiếp xúc với đường tròn, hay Δ là tiếp tuyến của đường tròn (O). Điểm H gọi là tiếp điểm của tiếp tuyến với đường tròn (O)
Như vậy nếu Δ là tiếp tuyến của (O) thì Δ vuông góc với bán kính đi qua tiếp điểm
Ta có OH = R
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì
+ Điểm đó cách đều hai tiếp điểm
+ Tia kẻ từ điểm đó đến tâm O là tia phân giác góc tạo bởi 2 tiếp tuyến
+ Tia kẻ từ tâm đi qua điểm đó là tia phân giác góc tạo bởi hai bán kính đi qua các tiếp điểm
+ Tia kẻ từ tâm đi qua điểm đó thì vuông góc với đoạn thẳng nối hai tiếp điểm tại trung điểm của đoạn thẳng đó.
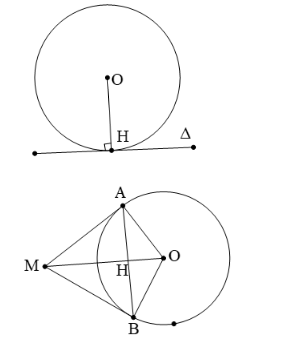
c) Đường thẳng và đường tròn không giao nhau
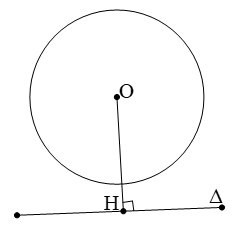
Khi một đường thẳng Δ và đường tròn (O) không có điểm chung ta nói đường thẳng Δ và đường tròn (O) không giao nhau. Khi đó OH > R
2. Hệ thức giữa khoảng cách từ tâm đường tròn đến đường thẳng và bán kính của đường tròn
| Vị trí tương đối của đường thẳng và đường tròn | Số điểm chung | Hệ thức giữa d và R |
| Đường thẳng và đường tròn cắt nhau | 2 | d < R |
| Đường thẳng và đường tròn tiếp xúc nhau | 1 | d = R |
| Đường thẳng và đường tròn không giao nhau | 0 | d > R |
3. Ví dụ cụ thể
Câu 1: Cho đường tròn tâm O bán kính bằng 6cm và một điểm A cách O 10cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính độ dài đoạn AB.
Hướng dẫn:
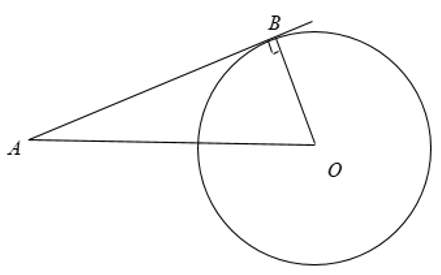
OA = 10cm ⇒ A nằm ngoài đường tròn
Ta có: AB là tiếp tuyến, B là tiếp điểm, khi đó OB = R = 6cm.
AB ⊥ OB áp dụng định lý Py – ta – go ta có:
AB2 + OB2 = OA2
![]()
Vậy AB = 8cm
Bài lý thuyết: Vị trí tương đối của đường thẳng và đường tròn trên đây các bạn học sinh cùng quý thầy cô cần nắm vững kiến thức về ba vị trí tương đối của đường thẳng và đường tròn, hệ thức giữa khoảng cách từ tâm đường tròn đến đường thẳng và bán kính của đường tròn ....
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 9: Vị trí tương đối của đường thẳng và đường tròn. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 9, Giải bài tập Toán lớp 9 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc







