Tính số đo cung và số đo góc trong đường tròn

Trong chương trình Toán lớp 9, chuyên đề “Tính số đo cung và số đo góc trong đường tròn” giữ vai trò rất quan trọng, giúp học sinh làm quen và thành thạo với các khái niệm cơ bản như: số đo cung, góc ở tâm, góc nội tiếp, cũng như các mối liên hệ đặc biệt trong đường tròn. Việc nắm vững kiến thức này không chỉ giúp học sinh giải nhanh các bài tập hình học mà còn tạo nền tảng chắc chắn cho những chuyên đề hình học nâng cao ở bậc THPT.

Bài viết sẽ hệ thống đầy đủ lý thuyết trọng tâm, công thức tính toán và các ví dụ minh họa chi tiết để học sinh dễ dàng tiếp thu. Đồng thời, phần bài tập tự luyện kèm hướng dẫn sẽ giúp các em rèn luyện kỹ năng giải toán, tăng khả năng tư duy logic và chuẩn bị vững vàng cho các kỳ kiểm tra, đặc biệt là kỳ thi vào lớp 10.

Ngoài ra, mời bạn đọc tham khảo một số nội dung đặc sắc trong chương trình Toán 9:

• Ôn thi vào lớp 10 chuyên đề 10: Chứng minh các hệ thức hình học
• Các dạng Toán thi vào 10
• Các bài toán Hình học ôn thi vào lớp 10

I. Một số kiến thức cần nhớ khi tính số đo góc và số đo cung trong đường tròn

1. Góc ở tâm

+ Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm

+ Nếu 0⁰ < a < 180⁰ thì cung nằm bên trong góc được gọi là cung nhỏ, cung nằm bên ngoài góc được gọi là cung lớn

2. Số đo cung

+ Số đo của cung AB được kí hiệu là sđ AB

+ Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó

+ Số đo của cung lớn bằng hiệu giữa 360⁰ và số đo của cung nhỏ

+ Nếu C là một điểm nằm trên cung AB thì sđ AB = sđ AC + sđ CB

3. Góc nội tiếp

+ Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó

+ Góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung

+ Góc nội tiếp chắn nửa đường tròn là góc vuông

4. Góc tạo bởi tia tiếp tuyến và dây cung

+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.

Hệ quả

Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau. \(\widehat{BAx} = \widehat{BCA}\).

Định lí đảo

Nếu \(\widehat{BAx}\) với đỉnh \(A\) nằm trên đường tròn. Một cạnh chứa dây cung \(AB\) có số đo bằng nửa số đo của cung \(AB\) căng dây đó và cung này nằm bên trong góc đó thì \(Ax\) là một tia tiếp tuyến của đường tròn.

5. Góc có đỉnh ở bên trong đường tròn

Hình vẽ minh họa

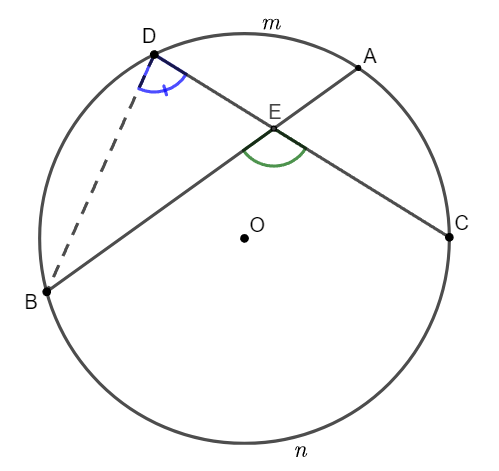
+ Số đo của góc có định ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

\(\widehat{BEC} = \frac{sd\widehat{BnC} + sd\widehat{AmD}}{2}\)

6. Góc có đỉnh ở bên ngoài đường tròn

Hình vẽ minh họa

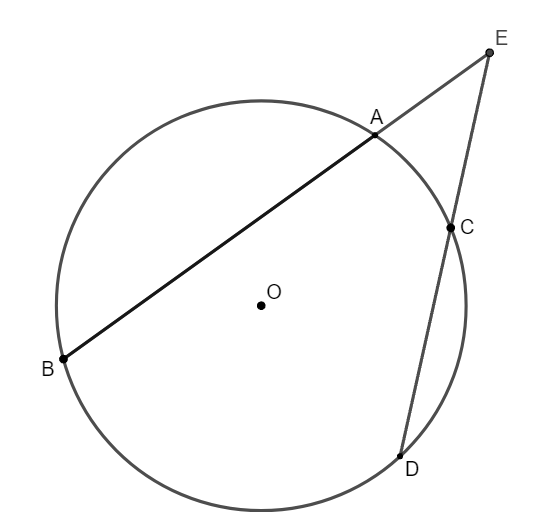
+ Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

\(\widehat{BEC} = \frac{sd\widehat{BC} - sd\widehat{AD}}{2}\)

II. Bài tập ví dụ cho các bài tập về tính số đo góc và số đo cung trong đường tròn

Bài 1: Cho tam giác nhọn \(ABC\) có \(\widehat{B} = 45^{0}\) . Vẽ đường tròn đường kính \(AC\) có tâm \(O\) , đường tròn này cắt \(BA;BC\) lần lượt tại \(D\) và \(E\) .

a) Chứng minh \(AE = EB\) .

b) Gọi \(H\) là giao điểm của \(CD\) và \(AE\) . Chứng minh rằng đường trung trực của đoạn \(HE\) đi qua trung điểm \(I\) của \(BH\) .

c) Chứng minh \(BH\bot AC\) .

Hướng dẫn giải

Hình vẽ minh họa

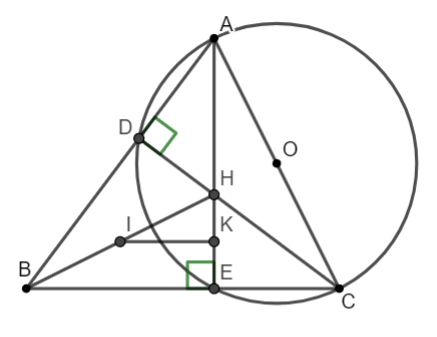
a) Ta có: \(\widehat{AEC} = 90^{0}\) (góc nội tiếp chắn nửa đường tròn)

\(\Rightarrow \widehat{AEB} = 90^{0}\)

Theo giả thiết \(\widehat{B} = 45^{0}\)

Suy ra tam giác \(AEB\) vuông cân tại \(E\)

\(\Rightarrow AE = EB\)

b) Gọi \(K\) là trung điểm của \(HE\)

Xét tam giác \(BHE\) có \(I\) là trung điểm của \(HB\) ; \(K\) là trung điểm của \(HE\)

Suy ra \(IK\) là đường trung bình của tam giác \(HBE\)

\(\Rightarrow IK//BE\)

Mặt khác \(\widehat{AEB} = 90^{0}\) (chứng minh trên) \(\Rightarrow BE\bot HE \equiv E\)

\(\Rightarrow IK\bot HE \equiv K\)

Vậy \(IK\) là đường trung trực của \(HE\) .

c) Theo chứng minh trên ta có: \(\widehat{AEC} = 90^{0} \Rightarrow AE\bot BC\)

Suy ra \(AE\) là đường cao hạ từ đỉnh \(A\) của tam giác \(ABC\) (*)

Ta có: \(\widehat{ADC} = 90^{0}\) (góc nội tiếp chắn nửa đường tròn)

\(\Rightarrow CD\bot AB\)

Suy ra \(CD\) là đường cao hạ từ đỉnh \(C\) của tam giác \(ABC\) (**)

Từ (*) và (**) và \(H\) là giao điểm của \(CD\) và \(AE\)

Suy ra \(H\) là trực tâm của tam giác \(ABC\)

\(\Rightarrow BH\bot AC\) (điều phải chứng minh)

Bài 2: Cho đường tròn \((O;R)\) đường kính \(AB\) . Kẻ tiếp tuyến \(Ax\) và lấy trên tiếp tuyến đó một điểm \(P\) sao cho \(AP > R\) , từ \(P\) kẻ tiếp tuyến tiếp xúc với \((O)\) tại \(M\) .

a) Chứng minh \(BM//OP\) .

b) Đường thẳng vuông góc với \(AB\) ở \(O\) cắt tia \(BM\) tại \(N\) . Chứng minh tứ giác \(OBPN\) là hình bình hành.

c) Biết \(AN\) cắt \(OP\) tại \(K\) , \(PM\) cắt \(ON\) tại \(I\) , \(PN\) và \(OM\) kéo dài cắt nhau \(J\) . Chứng minh \(I;J;K\) thẳng hàng.

Hướng dẫn giải

Hình vẽ minh họa

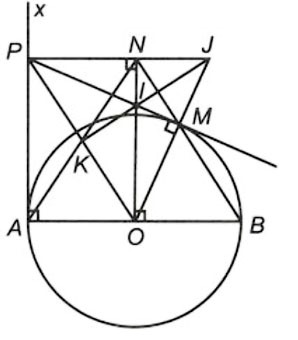
a) Ta có: \(\widehat{ABM}\) nội tiếp chắn cung \(\widehat{AM}\) ; \(\widehat{AOM}\) ở tâm chắn cung \(\widehat{AM}\)

\(\Rightarrow \widehat{ABM} = \frac{\widehat{AOM}}{2}(*)\)

Theo tính chất hai tiếp tuyến cắt nhau ta có:

\(\widehat{AOP} = \widehat{POM} \Rightarrow \widehat{AOP} = \frac{\widehat{AOM}}{2}(**)\)

Từ (*) và (**) suy ra \(\widehat{ABM} = \widehat{AOP}\)

Mà \(\widehat{ABM};\widehat{AOP}\) là hai góc đồng vị nên \(BM//OP(1)\)

b) Xét hai tam giác \(AOP\) và tam giác \(OBN\) ta có:

\(\widehat{PAO} = \widehat{NOB} = 90^{0}\)

\(OA = OB = R\)

\(\widehat{AOP} = \widehat{OBN}\) (chứng minh câu a)

Do đó \(\Delta AOP = \Delta OBN(g - c - g)\)

\(\Rightarrow OP = BN(2)\)

Từ (1) và (2) suy ra tứ giác \(OBPN\) là hình bình hành (vì có hai cạnh đối song song và bằng nhau)

c) Tứ giác \(OBPN\) là hình bình hành suy ra \(PN//OB\) hay \(PJ//AB\) .

Mà \(ON\bot AB \Rightarrow ON\bot PJ\)

Ta cũng có \(PM\bot OJ\) ( \(PM\) là tiếp tuyến)

Mà \(ON \cap PM \equiv I\) nên \(I\) là trực tâm tam giác \(POJ \Rightarrow IJ\bot OP(3)\)

Dễ thấy tứ giác \(AONP\) là hình chữ nhật vì có \(\widehat{PAO} = \widehat{AON} = \widehat{ONP} = 90^{0}\)

Suy ra \(K\) là trung điểm của \(PO\) .

\(AONP\) là hình chữ nhật suy ra \(\widehat{APO} = \widehat{NOP}\)

Theo tính chất hai tiếp tuyến cắt nhau ta có \(PO\) là tia phân giác của \(\widehat{APM}\)

\(\Rightarrow \widehat{APO} = \widehat{MPO}\)

\(\Rightarrow \widehat{OPI} = \widehat{IOP}\)

Suy ra tam giác \(OIP\) cân tại \(I\) .

Mặt khác \(K\) là trung điểm của \(OP \Rightarrow IK\bot OP(4)\)

Từ (3) và (4) suy ra \(I;J;K\) thẳng hàng (điều phải chứng minh)

Bài 3: Cho M, N, P, Q là bốn điểm tùy ý trên đường tròn (O). Các tiếp tuyến của (O) tại bốn điểm trên cắt nhau tạo thành tứ giác ABCD. Tính số đo tổng các góc \(\widehat {AOB} + \widehat {COD}\).

Lời giải:

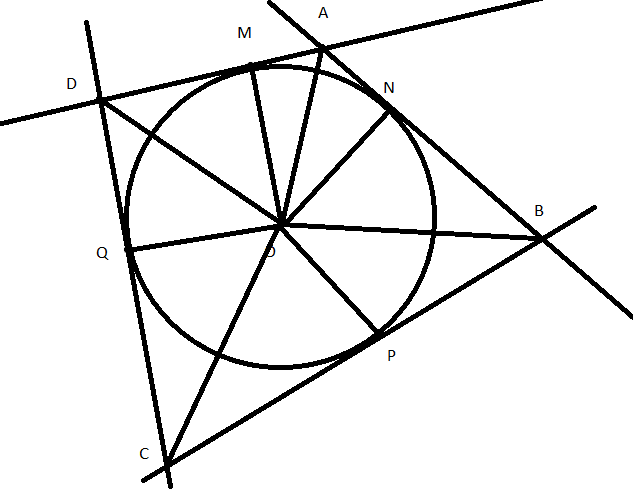
+ Xét đường tròn (O) có: tiếp tuyến NB và PB cắt nhau tại B nên OB là tia phân giác của \(\widehat {NOP} \Rightarrow \widehat {NOB} = \frac{1}{2}\widehat {NOP}\) (1)

+ Tương tự như vậy ta cùng có \(\widehat {AON} = \frac{1}{2}\widehat {MON}\)(2); \(\widehat {DOQ} = \frac{1}{2}\widehat {MOQ}\)(3) và \(\widehat {COQ} = \frac{1}{2}\widehat {QOP}\)(4)

+ Từ (1), (2), (3) và (4) có:

\(\left( {\widehat {AON} + \widehat {NOB}} \right) + \left( {\widehat {DOQ} + \widehat {QOC}} \right)\)

\(= \frac{1}{2}\widehat {MON} + \frac{1}{2}\widehat {NOP} + \frac{1}{2}\widehat {MOQ} + \frac{1}{2}\widehat {QOP}\)

\(\Leftrightarrow \widehat {AOB} + \widehat {DOC} = \frac{1}{2}{.360^0} = {180^0}\)

Bài 4: Cho tam giác cân AOB, có góc AOB bằng 110 độ. Vẽ đường tròn tâm O, bán kính OA. Gọi C là một điểm trên đường tròn (O), biết số đo cung AC bằng 40 độ. Tính số đo của cung nhỏ BC và cung lớn BC.

Lời giải:

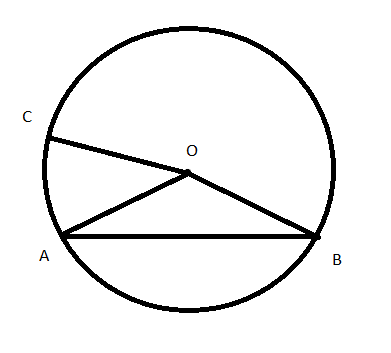
+ Số đo của cung AC bằng 40 độ \(\Rightarrow \widehat {AOC} = {40^0}\)

+ Có \(\widehat {AOC} + \widehat {AOB} = {40^0} + {110^0} = {150^0}\)

Vậy số đo của cung nhỏ BC là: 150⁰

Số đo của cung lớn BC là: 360⁰ – 150⁰ = 210⁰

Bài 5: Cho hình vuông ABCD nội tiếp trong đường tròn (O). M điểm bất kì trên cung nhỏ CD; MB cắt AC tại E.

a, Chứng minh tứ giác DMEO nội tiếp đường tròn.

b, Tính đo của góc DMC.

Hướng dẫn giải 

Hình vẽ minh họa

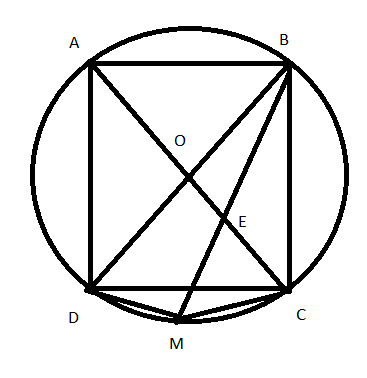
a, + Có \(\widehat {DMB}\) nhìn đường kính BD nên \(\widehat {DMB} = {90^0}\)

+ Có ABCD là hình vuông, tâm tại O \(\Rightarrow AC \bot BD \Rightarrow \widehat {DOE} = {90^0}\)

+ Xét tứ giác DOEM có: \(\widehat {DMB} + \widehat {DOE} = {90^0} + {90^0} = {180^0}\)

Suy ra tứ giác DOEM nội tiếp đường tròn

b, + Ta có ABCD là hình vuông đồng thời là hình thoi

Suy ra AC và BD là phân giác của các góc A, B, C và D

\(\Rightarrow \widehat {BAC} = \frac{{{{90}^0}}}{2} = {45^0}\)

Mà \(\widehat {BMC} = \widehat {BAC}\) (góc nội tiếp chắn cung BC). Suy ra \(\widehat {BMC} = {45^0}\)

+ Có \(\widehat {DMC} = \widehat {BMD} + \widehat {BMC} = {90^0} + {35^0} = {135^0}\).

Bài 6. BC là một dây cung của đường tròn (O; R) (BC \(\neq\) 2R). Điểm A di động trên cung lớn BC sao cho O luôn nằm trong tam giác ABC. Các đường cao AD, BE, CF của tam giác ABC đồng quy tại H.

1. Chứng minh tam giác AEF đồng dạng với tam giác ABC.

2. Gọi A’ là trung điểm của BC, Chứng minh AH = 2OA’.

3. Gọi A₁ là trung điểm của EF, Chứng minh R.AA₁ = AA’. OA’.

4. Chứng minh R(EF + FD + DE) = 2S_ABC suy ra vị trí của A để tổng EF + FD + DE đạt giá trị lớn nhất.

Hướng dẫn giải

Hình vẽ minh họa

 

1. Tứ giác BFEC nội tiếp

=> ∠AEF = ∠ACB (cùng bù ∠BFE)

∠AEF = ∠ABC (cùng bù ∠CEF) => ∆ AEF ∼ ∆ ABC.

2. Vẽ đường kính AK => KB // CH ( cùng vuông góc AB); KC // BH (cùng vuông góc AC) => BHKC là hình bình hành

=> A’ là trung điểm của HK => OK là đường trung bình của ∆AHK => AH = 2OA’.

3. Áp dụng tính chất: Nếu hai tam giác đồng dạng thì tỉ số giữa hia trung tuyến, tỉ số giữa hai bán kính các đường tròn ngoại tiếp bằng tỉ số đồng dạng.

Ta có: ∆ AEF ∼ ∆ ABC => \(\frac{R}{R'}\ = \ \frac{AA'}{AA_{1}}\) (1) trong đó R là bán kính đường tròn ngoại tiếp ∆ABC; R’ là bán kính đường tròn ngoại tiếp ∆ AEF; AA’ là trung tuyến của ∆ABC; AA₁ là trung tuyến của ∆AEF.

Tứ giác AEHF nội tiếp đường tròn đường kính AH nên đây cũng là đường tròn ngoại tiếp ∆AEF

Từ (1) => R.AA₁ = AA’. R’ = AA’ \(\frac{AH}{2}\) = AA’ . \(\frac{2A'O}{2}\)

Vậy R . AA₁ = AA’ . A’O (2)

4. Gọi B’, C’ lần lượt là trung điểm của AC, AB, ta có OB’⊥AC ; OC’⊥AB (bán kính đi qua trung điểm của một dây không qua tâm) => OA’, OB’, OC’ lần lượt là các đường cao của các tam giác OBC, OCA, OAB.

S_ABC = S_OBC+ S_OCA + S_OAB =\(\frac{1}{2}\)( OA’ . BC’ + OB’ . AC + OC’ . AB )

2S_ABC = OA’ . BC + OB’ . AC’ + OC’ . AB (3)

Theo (2) => OA’ = R . \(\frac{AA_{1}}{AA'}\) mà \(\frac{AA_{1}}{AA'}\) là tỉ số giữa 2 trung tuyến của hai tam giác đồng dạng AEF và ABC nên \(\frac{AA_{1}}{AA'}\) = \(\frac{EF}{BC}\).

Tương tự ta có: OB’ = R .\(\frac{FD}{AC}\); OC’ = R . \(\frac{ED}{AB}\)

Thay vào (3) ta được

2S_ABC = R (\(\frac{EF}{BC}.BC + \frac{FD}{AC}.AC + \frac{ED}{AB}.AB\)) ⬄ 2S_ABC = R(EF + FD + DE)

* R(EF + FD + DE) = 2S_ABC mà R không đổi nên (EF + FD + DE) đạt gí trị lớn nhất khi S_ABC.

Ta có S_ABC = \(\frac{1}{2}\)AD.BC do BC không đổi nên S_ABC lớn nhất khi AD lớn nhất, mà AD lớn nhất khi A là điểm chính giữa của cung lớn BC

III. Bài tập tự luyện các bài toán về tính số đo góc và số đo cung trong đường tròn

Bài 1: Trên đường tròn tâm O lấy ba điểm M, N, P sao cho \(\widehat {MON} = {120^0}\), số đo cung MP bằng 50⁰. Tính số đo cung nhỏ PN và số đo cung lớn PN trong các trường hợp điểm P nằm trên cung nhỏ MN.

Bài 2: Cho hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M, biết \(\widehat {AMB} = {40^0}\)

a, Tính \(\widehat {AMO};\widehat {AOM}\).

b, Tính số đo cung AB nhỏ và cung AB lớn.

Bài 3: Từ điểm A trên đường tròn (O), vẽ tiếp tuyến d với đường tròn. Trên d lấy điểm M sao cho AM = OA. Tính số đo góc ở tâm AOB.

Bài 4: Cho tam giác ABC có góc B bằng 70⁰, góc C bằng 50⁰ nội tiếp trong đường tròn (O). Tính:

a, Số đo của cung BC.

b, Gọi AD, BE, CF lần lượt là các đường phân giác của các góc A, B, C. Tính

1, Số đo các góc BEC, BED và FDE.

2, Số đo các cung CBF và BCE.

Bài 5: Cho tam giác ABC có ba góc nhọn. Vẽ đường tròn tâm O đường kính BC lần lượt cắt AB, AC tại D và E. BE cắt CD tại H. Biết số đo cung DE bằng 60⁰

a, Tính số đo của góc A và số đo của góc BHC.

b, Chứng minh AD.AB = AE.AC.

-------------------------------------------------

Tóm lại, việc tính số đo cung và số đo góc trong đường tròn không chỉ đơn thuần là một chuyên đề hình học lớp 9 mà còn là kiến thức nền tảng xuyên suốt quá trình học Toán. Bằng cách nắm chắc công thức, hiểu rõ mối quan hệ giữa cung – góc – đường tròn và thường xuyên luyện tập, học sinh sẽ hình thành tư duy toán học mạch lạc, giải quyết nhanh gọn nhiều dạng bài tập từ cơ bản đến nâng cao.

Với hệ thống lý thuyết, ví dụ minh họa và bài tập có lời giải chi tiết trong chuyên đề “Chuyên đề Toán lớp 9 luyện thi vào lớp 10”, các em sẽ có thêm hành trang vững chắc để tự tin chinh phục mọi kỳ thi. Ngoài ra, việc kết hợp luyện tập nhiều dạng bài tập khác nhau sẽ giúp học sinh củng cố kiến thức, rèn kỹ năng suy luận hình học và đạt kết quả cao trong học tập.