Chứng minh tứ giác nội tiếp một đường tròn
Chuyên đề luyện thi vào 10: Chứng minh tứ giác nội tiếp
Chứng minh tứ giác nội tiếp lớp 9 là một dạng toán thường gặp trong đề thi tuyển sinh vào lớp 10 môn Toán được VnDoc biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.
- Chuyên đề Tứ giác nội tiếp Toán 9 (Có đáp án)
- Tứ giác nội tiếp
- 6 Cách chứng minh tứ giác nội tiếp đường tròn
Bài tập về cách chứng minh tứ giác nộ tiếp được VnDoc biên soạn gồm hướng dẫn giải chi tiết cho dạng bài liên qua đến việc chứng minh tứ giác nội tiếp và tổng hợp các bài toán để các bạn học sinh có thể luyện tập thêm. Qua đó sẽ giúp các bạn học sinh ôn tập các kiến thức, chuẩn bị cho các bài thi học kì và ôn thi vào lớp 10 hiệu quả nhất. Sau đây mời các bạn học sinh cùng tham khảo tải về bản đầy đủ chi tiết.
I. Cách chứng minh tứ giác nội tiếp
+ Chứng minh tứ giác có hai góc vuông cùng nhìn một cạnh hoặc một đườn chéo (tâm đường tròn ngoại tiếp tứ giác được xác định là trung điểm của cạnh hoặc đường chéo đó)
+ Chứng minh tứ giác có tổng hai góc đối bằng 180º
+ Chứng minh tứ giác có hai góc bằng nhau cùng nhìn một cạnh
+ Chứng minh bốn đỉnh của tứ giác cùng cách đều một điểm
+ Chứng minh nếu tứ giác ABCD có AB cắt CD tại M mà MA.MB = MC.MD thì tứ giác ABCD nội tiếp, hoặc hai đường chéo cắt nhau tại O thỏa mãn OA.OC = OB.OD thì ABCD là tứ giác nội tiếp
II. Bài tập về cách chứng minh tứ giác nội tiếp
Bài 1: Cho điểm A nằm bên ngoài đường tròn (O). Từ A kể hai tếp tuyến AB, AC với đường tròn đó (B, C là các tiếp điểm). Chứng minh ABOC là tứ giác nội tiếp
Lời giải:
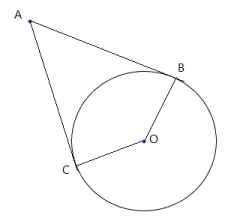
Ta có AB là tiếp tuyến của đường tròn (O) 
\(\Rightarrow \widehat {AOB} = {90^0}\)
Ta có AC là tiếp tuyến của đường tròn (O) \(\Rightarrow \widehat {AOC} = {90^0}\)
Xét tứ giác ABOC có: \(\widehat {AOB} + \widehat {AOC} = {90^0} + {90^0} = {180^0}\)
Suy ra tứ giác ABOC là tứ giác nội tiếp (tổng 2 góc đối bằng 180º)
Bài 2: Cho tam giác ABC không có góc tù. Đường cao AH và đường trung tuyến AM không trùng với nhau. Gọi N là trung điểm của AB. Cho biết \(\widehat {BAH} = \widehat {CAM}\). Chứng minh AMHN là tứ giác nội tiếp
Lời giải:
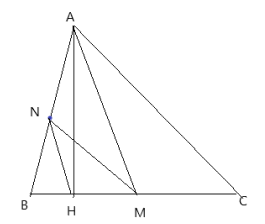
Xét tam giác ABC có N là trung điểm của AB, M là trung điểm của BC
Suy ra MN là đường trung bình của tam giác ABC, suy ra MN // AC
\(\Rightarrow \widehat {CAM} = \widehat {AMN}\)(so le trong)
Mà \(\widehat {BAH} = \widehat {CAM}\)
Suy ra \(\widehat {BAH} = \widehat {AMN}\) (1)
Có tam giác ABH vuông tại H, N là trung điểm của AB
Suy ra HN = AN = BN \(\Rightarrow \Delta AHN\)cân tại N \(\Rightarrow \widehat {BAH} = \widehat {AHN}\)(2)
Từ (1) và (2) suy ra \(\widehat {AMN} = \widehat {AHN}\)
Xét tứ giác AMHN có \(\widehat {AMN} = \widehat {AHN}\)
\(\widehat {AMN}\)nhìn cạnh AN
\(\widehat {AHN}\)nhìn cạnh AN
Vậy tứ giác AMHN là tứ giác nội tiếp
Bài 3: Cho tam giác đều ABC có đường cao AH, lấy điểm M tùy ý thuộc HC (M không trùng với H, C). Hình chiếu vuông góc của M lên AB, AC tại P và Q. Chứng minh APMQ là tứ giác nội tiếp và xác định tâm O của đường tròn ngoại tiếp tứ giác đó
Lời giải:
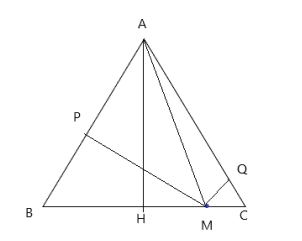
Có AP vuông góc với PM \(\Rightarrow \widehat {APM} = {90^0} \Rightarrow\) 3 điểm A, P, M cùng thuộc đường tròn đường kính AM
Có MQ vuông góc với AQ \(\Rightarrow \widehat {AQM} = {90^0} \Rightarrow\) 3 điểm A, Q, M cùng thuộc đường tròn đường kính AM
Vậy 4 điểm A, Q, M, P cùng thuộc một đường tròn hay tứ giác AQMP nội tiếp đường tròn đường kính AM, tâm của đường tròn là trung điểm của AM
Bài 4: Cho (O) đường kính AB, trên tia AB lấy điểm C bên ngoài đường tròn. Từ C kẻ CD vuông góc với AC và CD = AC. Nối AD cắt đường tròn (O) tại M. Kẻ BD cắt đường tròn (O) tại N
a, Chứng minh ANCD là tứ giác nội tiếp
b, Xác định đường kính và tâm của đường tròn ngoại tiếp tứ giác ANCD
Lời giải:
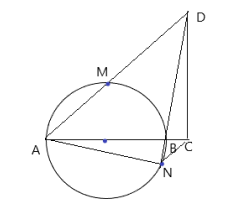
a, Có AD vuông góc với AC \(\Rightarrow \widehat {ACD} = {90^0} \Rightarrow\) 3 điểm A, C, D cùng thuộc đường tròn đường kính AD (1)
Có \(\widehat {ANB}\) nhìn đường kính AB nên \(\widehat {ANB} = {90^0}\)
Xét tam giác AND có \(\widehat {ANB} = {90^0} \Rightarrow\) Tam giác AND nội tiếp đường tròn đường kính AD, suy ra 3 điểm A, N, D cùng thuộc đường tròn đường kính AD (2)
Từ (1) và (2) suy ra 4 điểm A, C, N, D cùng thuộc đường tròn đường kính AD
b, Tứ giác ANCD nội tiếp đường tròn đường kính AD
Lại có M là trung điểm của AD nên đường tròn ngoại tiếp tứ giác ANCD là đường tròn tâm M, đường kính AD
Bài 5: Cho nửa đường tròn đường kính AB và dây AC. Từ một điểm D trên AC, vẽ DE vuông góc với AB. Chứng minh rằng BCDE là tứ giác nội tiếp
Lời giải
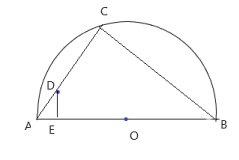
Có \(\widehat {ACB}\) nhìn đường kính AB \(\Rightarrow \widehat {ACB} = {90^0}\)
Có DE vuông góc với AB \(\Rightarrow \widehat {DEB} = {90^0}\)
Xét tứ giác BCDE có \(\widehat {ACB} + \widehat {DEB} = {90^0} + {90^0} = {180^0}\)
\(\Rightarrow\)Tứ giác BDCE nội tiếp đường tròn
III. Bài tập tự luyện chuyên đề chứng minh tứ giác nội tiếp
Bài 1: Cho tam giác ABC vuông tại A. Điểm E di dộng trên canh AB. Qua B vẽ một đường thẳng vuông góc với tia CE tại D và cắt tia CA tại H. Chứng minh tứ giác ADBC nội tiếp
Bài 2: Cho nửa đường tròn (O) đường kính AB và tia tiếp tuyến Bx của nửa đường tròn. Trên tia Bx lấy hai điểm C và D (C nằm giữa B và D). Các tia AC và BD lần lượt cắt đường tròn tại E và F. Hai dây AE và BF cắt nhau tại M. Hai tia AF và BE cắt nhau tại N. Chứng minh rằng
a, Tứ giác FNEM nội tiếp
b, Tứ giác CDFE nội tiếp
Bài 3: Cho tam giác ABC. Hai đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC. Chứng minh rằng tứ giác ABDC nội tiếp được đường tròn. Xác định tâm O của đường tròn đó
Bài 4: Cho tam giác ABC vuông ở A có AH là đường cao và BE là đường phân giác (H thuộc BC, E thuộc AC). Kẻ AD vuông góc với BE tại D. Chứng minh rằng tứ giác ABHD nôi tiếp đường tròn (O)
Bài 5: Từ một điểm M ở bên ngoài đường tròn (O), ta vẽ hai tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB lấy một điểm C. Vẽ CD, C, CF lần lượt vuông góc với AB, MA, MB. Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. Chứng minh tứ giác AECD, BFCD nội tiếp
Bài 6: Cho đường tròn (O), đường kính AB. Từ một đểm N thuộc tia đối của tia AB, vẽ tiếp tuyến MC, MD (C, D là các tiếp điểm). Vẽ CE vuông góc với DB tại E. Gọi F là trung điểm của CE; BF cắt (O) tại điểm thứ hai là G. H là giao điểm của Ab và CD. Chứng minh:
a, Tứ giác CGHF nội tiếp
b, Tứ giác MGHD nội tiếp
Bài 7: Cho tam giác ABC nhọn nội tiếp trong đường tròn tâm O (AB < AC). Từ B và C kẻ hai tiếp tuyến vào đường tròn cắt nhau tại M. MA cắt đường tròn (O) tại D (D khác A). Chứng minh tứ giác OBMC nội tiếp đường tròn
Bài 8: Cho đường tròn (O; R) và dây cung BC không đi qua tâm. Gọi A là điểm chính giữa của cung nhỏ BC. Góc nội tiếp quay quanh điểm A và có số đo không đổi sao cho E, F khác phía với điểm A so với BC; AF và AE cắt đường thẳng BC lần lượt tại M và N. Lấy điểm D sao cho tứ giác MNED là hình bình hành. Chứng minh MNEF là tứ giác nội tiếp
Bài 9: Cho nửa đường tròn (O; R), đường kính AB, kẻ tiếp tuyến Ax và lấy trên tiếp tuyến đó một điểm P sao cho AP > R, từ P kẻ tiếp tuyến với (O) tại M. Chứng minh rằng tứ giác APMO nội tiếp
Bài 10: Cho nửa đường tròn đường kính BC = 2R. Từ điểm A trên nửa đường tròn vẽ AH vuông góc với BC. Nửa đường tròn đường kính BH, CH lần lượt có tâm O1 và O2, cắt AB, AC theo thứ tự tại D và E. Chứng minh tứ giác BDEC nội tiếp đường tròn.
Bài 11 (Nâng cao):
Cho tứ giác ABCD nội tiế đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc với AD. Chứng minh:
a. Tứ giác EBEF, tứ giác DCEF nội tiếp.
b. CA là phân giác của \(\widehat{BCF}\)
c. Gọi M là trung điểm của DE. Chứng minh tứ giác BCMF nội tiếp.
Bài 12 (Nâng cao) :
Tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường chéo AC, BD cắt nhau tại E. Hình chiếu vuông góc của E trên AD là F. Đường thẳng CF cắt đường tròn tại điểm thứ hai là M. Giao điểm của BD và CF là N. Chứng minh:
a. CEFD là tứ giác nội tiếp
b. Tia FA là phân giác của góc BFM
c. BE.DN = EN.BD.
Bài 13 (Nâng cao) :
Cho tam giác ABC vuông ở A và một điểm D nằm giữa A và B. Đường tròn đường kính BD cắt BC tại E. Các đường thẳng CD, AE lần lượt cắt đường tròn tại các điểm thứ hai F, G. Chứng minh:
a. Tam giác ABC đồng dạng với tam giác EBD
b. Tứ giác ADEC và AFBC nội tiếp được một đường tròn
c. AC song song với FG
d. Các đường thẳng AC, DE, BF đồng quy.
Bài 14 (Nâng cao) :
Cho tam giác ABC có \(\widehat{A} =
90^{0}\); AB > AC, và một điểm M nằm trên đoạn AC ( M không trùng với A và C). Gọi N và D lần lượt là giao điểm thứ hai của BC và MB với đường tròn đường kính MC; gọi S là giao điểm thứ hai giữa AD với đường tròn đường kính MC; T là giao điểm của MN và AB. Chứng minh:
a. Bốn điểm A, M, N, B cùng thuộc một đường tròn
b. CM là phân giác của góc BCS.
c. \(\frac{TA}{TD} =
\frac{TC}{TB}\)
Bài 15 (Nâng cao) :
Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Qua A dựng hai tiếp tuyến AM và AN với đường tròn (M, N là các tiếp điểm) và một cact tuyến bất kỳ cắt đường tròn tại P, Q. Gọi L là trung điểm của PQ.
a. Chứng minh 5 điểm: O, L, M, A, N cùng thuộc một đường tròn
b. Chứng minh LA là phân giác của góc MLN
c. Gọi I là giao điểm của MN và LA. Chứng minh: MA\(\ ^{2}\)= AI. AL
d. Gọi K là giao điểm của ML với (O). Chứng minh rằng: KN // AQ
e. Chứng minh tam giác KLN cân.
Bài 16 (Nâng cao):
Cho đường tròn (O; R) tiếp xúc với đường thẳng d tại A. Trên d lấy điểm H không trùng với điểm A và AH < R. Qua H kẻ đường thẳng vuông góc với d, đường thẳng này cắt đường tròn tại hai điểm E và B (E nằm giữa B và H)
a. Chứng minh: góc ABE bằng góc EAH và tam giác AHB đồng dạng với tam giác EAH.
b. Lấy điểm C trên d sao cho H lá trung điểm của đoạn AC, đường thẳng CE cắt AB tại K. Chứng minh: AHEK là tứ giác nội tiếp
c. Xác định vị trí của điểm H để AB = R\(\sqrt{3}\)
-------------------------
Các bạn tham khảo thêm:
Ngoài Chứng minh tứ giác nội tiếp một đường tròn. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2019 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt
