Chứng minh các tứ giác đặc biệt trong đường tròn

Trong hình học lớp 9, chứng minh các tứ giác đặc biệt trong đường tròn là một dạng toán quan trọng và thường xuyên xuất hiện trong các đề kiểm tra, đề thi vào lớp 10. Dạng toán này yêu cầu học sinh vận dụng linh hoạt các kiến thức về góc nội tiếp, góc tạo bởi tia tiếp tuyến và dây cung, định lý tứ giác nội tiếp, cùng các dấu hiệu nhận biết tứ giác đặc biệt như hình chữ nhật, hình thoi, hình vuông hoặc hình thang cân.

Việc nắm vững phương pháp chứng minh không chỉ giúp bạn giải nhanh và chính xác mà còn rèn luyện kỹ năng tư duy logic, khả năng trình bày chặt chẽ và khoa học. Bài viết này sẽ tổng hợp lý thuyết, phân tích phương pháp, đồng thời đưa ra ví dụ minh họa chi tiết giúp bạn dễ dàng chinh phục dạng toán này.

I. Cách chứng minh các tứ giác đặc biệt

1. Hình thang

+ Tứ giác có hai cạnh song song thì tứ giác ấy là hình thang

2. Hình thang cân

+ Hình thang có hai đường chéo bằng nhau

+ Hình thang có hai góc kề một đáy bằng nhau

+ Hình thang nội tiếp trong đường tròn

3. Hình thang vuông

+ Hình thang có một góc vuông

4. Hình bình hành

+ Tứ giác có 2 cặp cạnh đối song song

+ Tứ giác có 2 cặp cạnh đối bằng nhau

+ Tứ giác có 1 cặp cạnh đối song song và bằng nhau

+ Tứ giác có 2 cặp góc đối bằng nhau

+ Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường

5. Hình chữ nhật

+ Tứ giác có 3 góc vuông

+ Hình bình hành có một góc vuông

+ Hình bình hàng có hai đường chéo bằng nhau

+ Hình thang cân có một góc vuông

6. Hình thoi

+ Tứ giác có 4 cạnh bằng nhau

+ Hình bình hành có hai cạnh kề bằng nhau

+ Hình bình hành có hai đường chéo vuông góc với nhau

+ Hình bình hàng có một đường chéo là tia phân giác của một góc

7. Hình vuông

+ Hình chữ nhật có hai cạnh kề bằng nhau

+ Hình chữ nhật có hai đường chéo vuông góc

+ Hình chữ nhật có một đường chéo là tia phân giác

+ Hình thoi có một góc vuông

+ Hình thoi có hai đường chéo bằng nhau

II. Bài tập ví dụ cho bài toán chứng minh các tứ giác đặc biệt

Bài 1: Cho tam giác ABC vuông tại A (AB > AC), đường cao AH. Trên nửa mặt phẳng chứa A bờ BC vẽ nửa đường tròn tâm O đường kính BH cắt AB tại E và nửa đường tròn đường kính HC cắt AC tại F. Chứng minh tứ giác AEHF là hình chữ nhật

Lời giải:

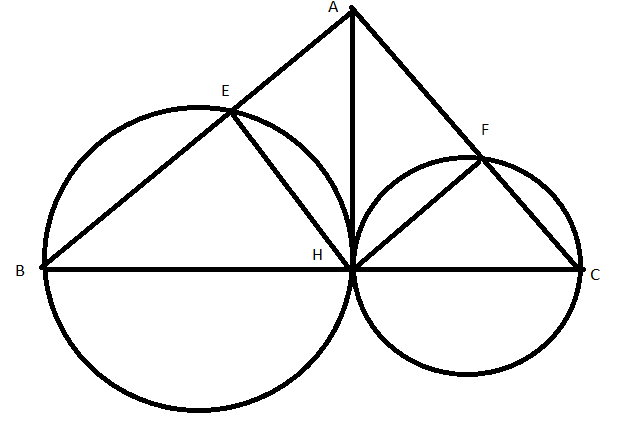
+ Có \(\widehat {BEH}\) nhìn đường kính BH nên \(\widehat {BEH} = {90^0}\)

+ Có \(\widehat {CFH}\) nhìn đường kính CH nên \(\widehat {CFH} = {90^0}\)

+ Xét tứ giác AEHF có:

\(\widehat {BAC} = {90^0};\widehat {BEH} = {90^0};\widehat {CFH} = {90^0}\)

Suy ra tứ giác AEHF là hình chữ nhật

Bài 2: Cho đường tròn (O; R), đường kính AB. Kẻ hai tia tiếp tuyến Ax, By với nửa đường tròn. Tiếp tuyến của nửa đường tròn tại M cắt Ax, By lần lượt tại C và D. Nối MA cắt OC tại E. Nối MB cắt OD tại F. Chứng minh tứ giác OEMF là hình chữ nhật

Lời giải:

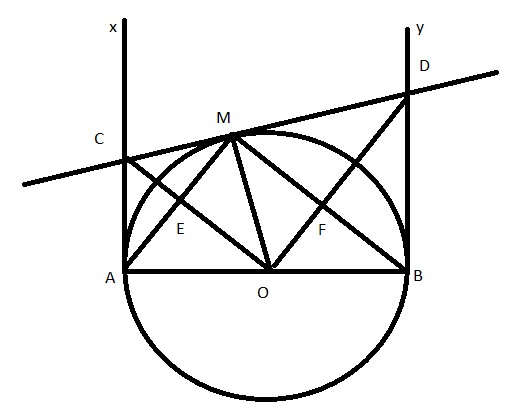
+ Có Ax và MC là hai tiếp tuyến cắt nhau tại C suy ra OC là tia phân giác của \(\widehat {AOM}\)

+ Có By và MD là hai tiếp tuyến cắt nhau tại D suy ra OD là tia phân giác của  \(\widehat {BOM}\)

+ Xét tam giác AOM có:

OA = OM nên tam giác AOM là tam giác cân

OC là tia phân giác của \(\widehat {AOM}\)

Suy ra OE vuông góc MA nên \(\widehat {OEM} = {90^0}\)

+ Xét tam giác BOM có:

OM = OB nên tam giác MOB là tam giác cân

OD là tia phân giác của \(\widehat {BOM}\)

Suy ra OF vuông góc MF nên \(\widehat {OFM} = {90^0}\)

+ Có \(\widehat {AMB}\) nhìn đường kính AB nên \(\widehat {AMB} = {90^0}\)

+ Xét tứ giác MEOF có:

\(\widehat {OEM} = {90^0};\widehat {OFM} = {90^0};\widehat {AMB} = {90^0}\)

Suy ra tứ giác MEOF là hình chữ nhật.

Bài 3 Cho đường tròn (O) bán kính R có hai đường kính AB và CD vuông góc với nhau. Trên đoạn thẳng AB lấy điểm M (M khác O). CM cắt (O) tại N. Đường thẳng vuông góc với AB tại M cắt tiếp tuyến tại N của đường tròn ở P.

Chứng minh:

1. Tứ giác OMNP nội tiếp.

2. Tứ giác CMPO là hình bình hành.

3. CM.CN không phụ thuộc vào vị trí của điểm M.

4. Khi M di chuyển trên đoạn thẳng AB thì P chạy trên đoạn thẳng cố định nào.

Lời giải:

Hình vẽ minh họa

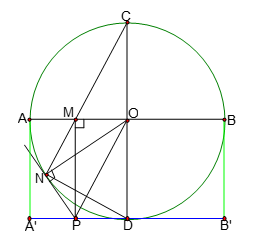
1. Ta có \(\widehat{OMP} = 90^{0}\) (vì \(PM\bot AB\)); \(\widehat{ONP} = 90^{0}\) (vì NP là tiếp tuyến ).

Như vậy M và N cùng nhìn OP dưới một góc bằng 90⁰ => M và N cùng nằm trên đường tròn đường kính OP => Tứ giác OMNP nội tiếp.

2. Tứ giác OMNP nội tiếp \(\Rightarrow \widehat{OPM} = \widehat{ONM}\) (nội tiếp chắn cung OM)

Tam giác ONC cân tại O vì có \(ON = OC = R \Rightarrow \widehat{ONC} = \widehat{OCN}\)

\(\Rightarrow \widehat{OPM} = \widehat{OCM}\)

Xét hai tam giác OMC và MOP ta có:

\(\widehat{MOC} = \widehat{OMP}\ = 90^{0};\widehat{OPM} = \widehat{OCM}\)

\(\Rightarrow \widehat{CMO} = \widehat{POM}\) lại có MO là cạnh chung \(\Rightarrow \Delta OMC = \Delta MOP \Rightarrow OC = MP\ \ \ (1)\)

Theo giả thiết ta có \(CD\bot AB;\ PM\bot AB \Rightarrow CO//PM\ \ (2)\)

Từ (1) và (2) => Tứ giác CMPO là hình bình hành.

3. Xét hai tam giác OMC và NDC ta có \(\widehat{MOC} = 90^{0}\) (giả thiết \(CD\bot AB\)); \(\widehat{DNC} = 90^{0}\) (nội tiếp chắn nửa đường tròn )

\(\ \Rightarrow \widehat{MOC} = \widehat{DNC}\ = 90^{0}\) lại có \(\widehat{C}\) là góc chung \(= > \Delta OMC\sim\Delta NDC\)

=> \(\frac{CM}{CD}\ = \ \frac{CO}{CN}\) => CM. CN = CO.CD mà CO = R; CD = 2R nên CO.CD = 2R² không đổi

=> CM.CN =2R² không đổi hay tích CM. CN không phụ thuộc vào vị trí của điểm M.

4. ( HD) Dễ thấy ∆OMC = ∆DPO (c.g.c) \(\Rightarrow \widehat{ODP} = 90^{0}\)=> P chạy trên đường thẳng cố định vuông góc với CD tại D.

Vì M chỉ chạy trên đoạn thẳng AB nên P chỉ chạy trên doạn thẳng A’ B’ song song và bằng AB.

Bài 4 Cho tam giác ABC vuông ở A (AB > AC), đường cao AH. Trên nửa mặt phẳng bờ BC chứa điển A , Vẽ nửa đường tròn đường kính BH cắt AB tại E, Nửa đường tròn đường kính HC cắt AC tại F

1. Chứng minh AFHE là hình chữ nhật.

2. BEFC là tứ giác nội tiếp.

3. AE. AB = AF. AC.

4. Chứng minh EF là tiếp tuyến chung của hai nửa đường tròn.

Hướng dẫn giải

Hình vẽ minh họa

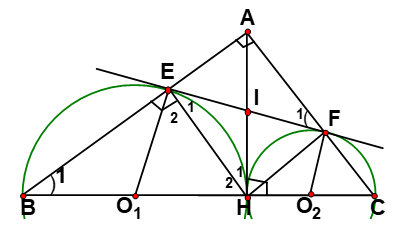
1. Ta có : \(\widehat{BEH} = 90^{0}\) ( nội tiếp chắn nửc đường tròn )

\(\Rightarrow \widehat{AEH} = 90^{0}\) (vì là hai góc kề bù). (1)

\(\widehat{CFH} = 90^{0}\) ( nội tiếp chắn nửc đường tròn )

\(\Rightarrow \widehat{AFH} = 90^{0}\) (vì là hai góc kề bù).(2)

\(\widehat{EAF} = 90^{0}\) (Vì tam giác ABC vuông tại A) (3)

Từ (1), (2), (3) => Tứ giác AFHE là hình chữ nhật ( vì có ba góc vuông).

2. Tứ giác AFHE là hình chữ nhật nên nội tiếp được một đường tròn =>éF₁=éH₁ (nội tiếp chắn cung AE) . Theo giả thiết AH ⊥BC nên AH là tiếp tuyến chung của hai nửa đường tròn (O₁) và (O₂)

\(\ \Rightarrow \widehat{B_{1}} = \widehat{H_{1}}\) (hai góc nội tiếp cùng chắn cung HE) \(\Rightarrow {\widehat{B}}_{1} = \widehat{F_{1}} \Rightarrow \widehat{EBC} + \widehat{EFC} = \widehat{AFE} + \widehat{EFC}\) mà \(\widehat{AFE} + \widehat{EFC} = 180^{0}\) (vì là hai góc kề bù) \(\Rightarrow \widehat{EBC} + \widehat{EFC} = 180^{0}\) mặt khác \(\widehat{EBC};\widehat{EFC}\) là hai góc đối của tứ giác BEFC do đó BEFC là tứ giác nội tiếp.

3. Xét hai tam giác AEF và ACB ta có éA = 90⁰ là góc chung; \(\widehat{AFE} = \widehat{ABC}\) (theo chứng minh trên)

=> ∆AEF ∼∆ACB => \(\frac{AE}{AC}\ = \ \frac{AF}{AB}\) => AE. AB = AF. AC.

* HD cách 2: Tam giác AHB vuông tại H có HE ⊥ AB => AH² = AE.AB (*)

Tam giác AHC vuông tại H có HF ⊥ AC => AH² = AF.AC (**)

Từ (*) và (**) => AE. AB = AF. AC

4. Tứ giác AFHE là hình chữ nhật => IE = EH => ∆IEH cân tại I \(\Rightarrow {\widehat{E}}_{1} = \widehat{H_{1}}\)

∆O₁EH cân tại O₁ (vì có O₁E vàO₁H cùng là bán kính) \(\Rightarrow \widehat{E_{2}} = \widehat{H_{2}}\)

\(\Rightarrow \widehat{E_{1}} + \widehat{E_{2}} = \widehat{H_{1}} + \widehat{H_{2}}\) mà \(\widehat{H_{1}} + \widehat{H_{2}} = \widehat{AHB} = 90^{0}\)

\(\Rightarrow {\widehat{E}}_{1} + \widehat{E_{2}} = \widehat{O_{1}EF} = 90^{0}\)

\(\Rightarrow O_{1}E\bot EF\).

Chứng minh tương tự ta cũng có \(O_{2}E\bot EF\).

Vậy EF là tiếp tuyến chung của hai nửa đường tròn .

Bài 5. Cho đường tròn (O) đường kính AC. Trên bán kính OC lấy điểm B tuỳ ý (B khác O, C ). Gọi M là trung điểm của đoạn AB. Qua M kẻ dây cung DE vuông góc với AB. Nối CD, Kẻ BI vuông góc với CD.

1. Chứng minh tứ giác BMDI nội tiếp .

2. Chứng minh tứ giác ADBE là hình thoi.

3. Chứng minh BI // AD.

4. Chứng minh I, B, E thẳng hàng.

5. Chứng minh MI là tiếp tuyến của (O’).

Hướng dẫn giải

Hình vẽ minh họa

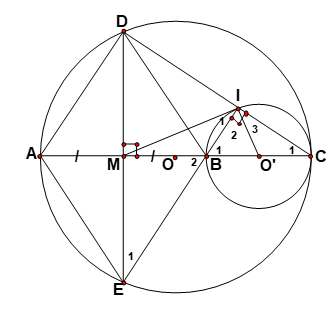
1. \(\widehat{BIC} = 90^{0}\) ( nội tiếp chắn nửa đường tròn ) \(\Rightarrow \widehat{BID} = 90^{0}\) (vì là hai góc kề bù); DE ⊥ AB tại M => Góc BMD = 90⁰

\(\Rightarrow \widehat{BID} + \widehat{BMD} = 180^{0}\)mà đây là hai góc đối của tứ giác MBID nên MBID là tứ giác nội tiếp.

2. Theo giả thiết M là trung điểm của AB; DE ⊥ AB tại M nên M cũng là trung điểm của DE (quan hệ đường kính và dây cung)

=> Tứ giác ADBE là hình thoi vì có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường .

3. \(\widehat{ADC} = 90^{0}\) ( nội tiếp chắn nửa đường tròn )

=> AD ⊥ DC; theo trên BI ⊥ DC => BI // AD. (1)

4. Theo giả thiết ADBE là hình thoi => EB // AD (2).

Từ (1) và (2) => I, B, E thẳng hàng (vì qua B chỉ có một đường thẳng song song với AD mà thôi.)

5. I, B, E thẳng hàng nên tam giác IDE vuông tại I

=> IM là trung tuyến ( vì M là trung điểm của DE) => MI = ME

=> ∆MIE cân tại M

\(\Rightarrow \widehat{I_{1}} = \widehat{E_{1}}\); ∆O’IC cân tại O’ ( vì O’C và O’I cùng là bán kính)

\(\ \Rightarrow {\widehat{I}}_{3} = \widehat{C_{1}}\) mà \(\widehat{C_{1}} = \widehat{E_{1}}\) (Cùng phụ với góc EDC)

\(\ \Rightarrow \widehat{I_{1}} = \widehat{I_{3}} \Rightarrow \widehat{I_{1}} + \widehat{I_{2}} = \widehat{I_{3}} + \widehat{I_{2}}\)

Mà \(\widehat{I_{3}} + \widehat{I_{2}} = \widehat{BIC} = 90^{0} \Rightarrow \widehat{I_{1}} + \widehat{I_{2}} = 90^{0} = \widehat{MIO}\) hay MI ⊥ O’I tại I

=> MI là tiếp tuyến của (O’).

Bài 6 Cho tam giác ABC nội tiếp (O). Gọi H là trực tâm của tam giác ABC; E là điểm đối xứng của H qua BC; F là điểm đối xứng của H qua trung điểm I của BC.

1. Chứng minh tứ giác BHCF là hình bình hành.

2. E, F nằm trên đường tròn (O).

3. Chứng minh tứ giác BCFE là hình thang cân.

4 Gọi G là giao điểm của AI và OH. Chứng minh G là trọng tâm của tam giác ABC.

Hướng dẫn giải

Hình vẽ minh họa

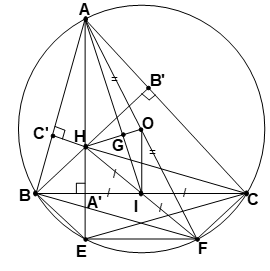
1. Theo giả thiết F là điểm đối xứng của H qua trung điểm I của BC => I là trung điểm BC và HE => BHCF là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường .

2. (HD) Tứ giác AB’HC’ nội tiếp \(\Rightarrow \widehat{BAC} + \widehat{B'HC} = 180^{0}\) mà

\(\widehat{BHC} = \widehat{B'HC'}\) (đối đỉnh) \(\Rightarrow \widehat{BAC} + \widehat{BHC} = 180^{0}\)

Theo trên BHCF là hình bình hành \(\Rightarrow \widehat{BHC} = \widehat{BFC} \Rightarrow \widehat{BFC} + \widehat{BAC} = 180^{0}\)

=> Tứ giác ABFC nội tiếp => F thuộc (O).

* H và E đối xứng nhau qua BC => ∆BHC = ∆BEC (c.c.c)

\(\Rightarrow \widehat{BHC} = \widehat{BEC} \Rightarrow \widehat{BEC} + \widehat{BAC} = 180^{0}\)

=> ABEC nội tiếp => E thuộc (O) .

3. Ta có H và E đối xứng nhau qua BC => BC ⊥ HE (1) và IH = IE mà I là trung điểm của của HF

=> EI = 1/2 HE => tam giác HEF vuông tại E hay FE ⊥ HE (2)

Từ (1) và (2) => EF // BC => BEFC là hình thang. (3)

Theo trên E ∈(O) \(\Rightarrow \widehat{CBE} = \widehat{CAE}\) (nội tiếp cùng chắn cung CE) (4).

Theo trên F ∈(O) và \(\widehat{FEA} = 90^{0}\)=> AF là đường kính của (O) \(\Rightarrow \widehat{ACF} = 90^{0} \Rightarrow \widehat{BCF} = \widehat{CAE}\)

( vì cùng phụ ∠ACB) (5).

Từ (4) và (5) \(\Rightarrow \widehat{BCF} = \widehat{CBE}\) (6).

Từ (3) và (6) => tứ giác BEFC là hình thang cân.

4. Theo trên AF là đường kính của (O) => O là trung điểm của AF; BHCF là hình bình hành => I là trung điểm của HF => OI là đường trung bình của tam giác AHF => OI = 1/ 2 AH.

Theo giả thiết I là trung điểm của BC => OI ⊥ BC (Quan hệ đường kính và dây cung) \(\Rightarrow \widehat{OIG} = \widehat{HAG}\) (vì so le trong); lại có \(\widehat{OGI} = \widehat{HGA}\) (đối đỉnh) => ∆OGI ∼ ∆HGA => \(\frac{GI}{GA}\ = \ \frac{OI}{HA}\) mà OI = \(\frac{1}{2}\) AH

=> \(\frac{GI}{GA}\ = \ \frac{1}{2}\) mà AI là trung tuyến của ∆ ABC (do I là trung điểm của BC)

=> G là trọng tâm của ∆ ABC.

Bài 7. Cho AB và AC là hai tiếp tuyến của đường tròn tâm O bán kính R ( B, C là tiếp điểm ). Vẽ CH vuông góc AB tại H, cắt (O) tại E và cắt OA tại D

1. Chứng minh CO = CD.

2. Chứng minh tứ giác OBCD là hình thoi.

3. Gọi M là trung điểm của CE, Bm cắt OH tại I. Chứng minh I là trung điểm của OH.

4. Tiếp tuyến tại E với (O) cắt AC tại K. Chứng minh ba điểm O, M, K thẳng hàng

Hướng dẫn giải

Hình vẽ minh họa

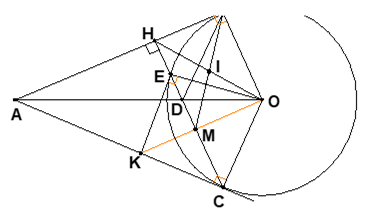
1. Theo giả thiết AB và AC là hai tiếp tuyến của đường tròn tâm O => OA là tia phân giác của ∠BOC => ∠BOA = ∠COA (1)

OB ⊥ AB ( AB là tiếp tuyến ); CH ⊥ AB (gt) => OB // CH => ∠BOA = ∠CDO (2)

Từ (1) và (2) => ∆COD cân tại C => CO = CD.(3)

2. Theo trên ta có CO = CD mà CO = BO (= R) => CD = BO (4) lại có OB // CH hay OB // CD (5)

Từ (4) và (5) => BOCD là hình bình hành (6) . Từ (6) và (3) => BOCD là hình thoi.

3. M là trung điểm của CE => OM ⊥ CE ( quan hệ đường kính và dây cung)

=> ∠OMH = 90⁰. theo trên ta cũng có ∠OBH =90⁰; ∠BHM =90⁰

=> Tứ giác OBHM là hình chữ nhật => I là trung điểm của OH.

4. M là trung điểm của CE; KE và KC là hai tiếp tuyến => O, M, K thẳng hàng.

Bài 8. Cho tam giác cân ABC ( AB = AC) nội tiếp đường tròn (O). Gọi D là trung điểm của AC; tiếp tuyến của đường tròn (O) tại A cắt tia BD tại E. Tia CE cắt (O) tại F.

1. Chứng minh BC // AE.

2. Chứng minh ABCE là hình bình hành.

3. Gọi I là trung điểm của CF và G là giao điểm của BC và OI. So sánh ∠BAC và ∠BGO.

Hướng dẫn giải

Hình vẽ minh họa

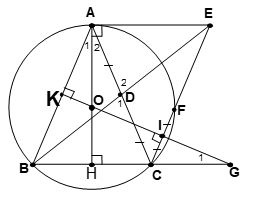
1. Học sinh tự thực hành làm

2. Xét hai tam giác ADE và CDB ta có ∠EAD = ∠BCD (vì so le trong)

AD = CD (giả thiết); ∠ADE = ∠CDB (đối đỉnh)

=> ∆ADE = ∆CDB => AE = CB (1)

Theo trên AE // CB (2) .Từ (1) và (2) => AECB là hình bình hành.

3. I là trung điểm của CF => OI ⊥ CF (quan hệ đường kính và dây cung).

Theo trên AECB là hình bình hành => AB // EC => OI ⊥ AB tại K

=> ∆BKG vuông tại K. Ta cung có ∆BHA vuông tại H

=> ∠BGK = ∠BAH ( cung phụ với ∠ABH) mà ∠BAH = \(\frac{1}{2}\)∠BAC (do ∆ABC cân nên AH là phân giác) => ∠BAC = 2∠BGO

III. Bài tập tự luyện về bài toán chứng minh các tứ giác đặc biệt

Bài 1: Cho nửa đường tròn đường kính AB. Từ AB kẻ tiếp tuyến Ax, By. Qua M thuộc nửa đường tròn, kẻ tiếp tuyến thứ ba cắt 2 tiếp tuyến Ax, By tại C và D. Chứng minh tứ giác ABCD là hình thang vuông.

Bài 2: Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Hai đường cao BE, CF cắt nhau tại H, tia AO cắt đường tròn (O) tại D. Chứng minh:

a, Tứ giác BCEF nội tiếp đường tròn.

b, Chứng minh tứ giác BHCD là hình bình hành.

Bài 3: Cho đường tròn (O; R) và một điểm A cách O một khoảng 2R. Từ A vẽ các tiếp tuyến AB, AC với đường tròn (B; C là các tiếp điểm). Đường thẳng vuông góc với Ob tại O cắt AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M. Chứng minh;

a, Tứ giác AMON là hình thoi.

b, Chứng minh MN là tiếp tuyến của đường tròn (O).

c, Tính diện tích hình thoi AMON.

Bài 4: Cho nửa đường tròn (O; R), đường kính AB trên nửa đường tròn lấy C (CA < CB). Hạ CH vuông góc với AB tại H. Đường tròn đường kính CH cắt CA và CB tại M và N. Chứng minh:

a, Tứ giác HMCN là hình chữ nhật.

b, Tứ giác AMNB nội tiếp.

Bài 5: Cho đường tròn tâm O. Gọi I là trung điểm của bán kính OA. Qua I kẻ dây BC vuông góc với OA. Chứng minh tứ giác ABOC là hình thoi.

Bài 6: Cho đường tròn tâm O bán kính R, hai đường kính AB và CD vuông góc với nhau. Trên đoạn AB lấy M, đường thẳng CM cắt (O) tại điểm thứ hai là N. Đường thẳng vuông góc với AB tại M cắt tiếp tuyến N của đường tròn tại P. Chứng minh:

a, Tứ giác OMNP nội tiếp.

b, Tứ giác CMPO là hình bình hành.

c, Tích CM.CN không đối.

Bài 7: Cho đường tròn (O) đường kính AB. Vẽ đường tròn (I) đường kính OA. Bán kính OC của đường tròn (O) cắt đường tròn (I) tại D. Vẽ CH vuông góc với AB. Chứng minh ACDH là hình thang cân

-------------------------------------------------------------

Dạng chứng minh các tứ giác đặc biệt trong đường tròn không chỉ là một phần quan trọng của chương trình Toán lớp 9 mà còn là “điểm gỡ” trong nhiều đề thi vào lớp 10. Thông qua việc luyện tập thường xuyên, bạn sẽ:

• Nhận diện nhanh dấu hiệu của các tứ giác đặc biệt.

• Áp dụng chính xác các định lý, tính chất của tứ giác nội tiếp và các mối quan hệ về góc, cạnh, đường chéo.

• Trình bày lời giải rõ ràng, logic và dễ hiểu, giúp giám khảo dễ dàng chấm điểm tối đa.

• Phát triển tư duy phân tích và khả năng kết hợp nhiều kiến thức hình học khác nhau.

Việc thành thạo chứng minh các tứ giác đặc biệt trong đường tròn sẽ giúp bạn tự tin hơn trong phòng thi, xử lý được cả những bài toán biến tấu, đồng thời tạo nền tảng vững chắc cho việc học toán ở bậc THPT. Hãy biến dạng toán này thành lợi thế điểm số của bạn bằng cách luyện tập đều đặn, ghi nhớ công thức, và rèn kỹ năng vẽ hình chính xác.