Chuyên đề Toán 9 Phép quay
Ứng dụng phép quay vào bài tập hình học lớp 9
Phép quay là một chuyên đề quan trọng trong chương trình Toán 9, đặc biệt trong phần hình học không gian và các bài toán liên quan đến phép biến hình. Trong bài viết này, chúng ta sẽ cùng tìm hiểu lý thuyết trọng tâm về phép quay, định nghĩa, tâm quay, góc quay, các tính chất cơ bản, cũng như cách vận dụng phép quay vào giải các bài toán hình học lớp 9. Tài liệu được biên soạn rõ ràng, dễ hiểu, kèm ví dụ minh họa cụ thể, giúp học sinh nắm chắc kiến thức và tự tin áp dụng vào các dạng đề thi.
A. Phép quay là gì?
Phép quay thuận chiều ![]() tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiếu kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo
tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiếu kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo ![]() (Hình a).
(Hình a).

Định nghĩa tương tự cho phép quay ngược chiều ![]() tâm O (Hình b). Phép quay
tâm O (Hình b). Phép quay ![]() và phép quay
và phép quay ![]() giữ nguyên mọi điểm.
giữ nguyên mọi điểm.
Tính chất phép quay Toán 9
- Một phép quay được gọi là giữ nguyên một đa giác đều H nếu phép quay đó biến mỗi điểm H thành một điểm của H.
- Người ta nghĩ ra rằng nếu một phép quay biến các đỉnh của đa giác đều H thành các đỉnh của H thì phép quay đó giữ nguyên
 .
.
B. Các dạng bài tập phép quay lớp 9
Bài toán 1. Cho lục giác đều ABCDEF.
a) Tính số đo các góc BCF, BDF, BEF.
b) Gọi O là tâm của lục giác đều. Hãy chỉ ra ba phép quay tâm O giữ nguyên tam giác ACE.
Hướng dẫn giải
Hình vẽ minh họa:

a) Dễ thấy ABCDEF là lục giác đều nên ![]()
![]() .
.
Ta có tứ giác ![]() nội tiếp đường tròn (R) nên
nội tiếp đường tròn (R) nên ![]() hay
hay ![]()
![]() .
.
Tương tự tứ giác ABDF nội tiếp đường tròn (R) nên ![]() hay
hay ![]()
![]() .
.
Tương tự ta có ![]() .
.
b) Ba đỉnh A; C; E của tam giác đều ACE chia đường tròn (O) thành ba cung bằng nhau: ![]() .
.
Do đó có 6 phép quay tâm O giữ nguyên tam giác đó là:
Phép quay 1200; 2400 thuận chiều hoặc 1200 ngược chiều.
Nhận xét: Có tất cả 6 phép quay 1200; 2400; 3600 tâm O thuận chiều hoặc ngược chiều kim đồng hồ giữ nguyên tam giác.
Bài toán 2. Cho tam giác ABC đều như hình vẽ. Điểm B biến thành điểm nào:
a) Phép phép quay thuận chiều 600 tâm A.
b) Phép phép quay ngược chiều 3000 tâm A.
Hướng dẫn giải
Hình vẽ minh họa:

a) Tam giác ABC đều nên AB = AC. Do đó C thuộc đường tròn (A; AB).
Xét đường tròn (A; AB), ta có: ![]()
![]()
Khi đó điểm B biến thành điểm C qua phép quay thuận chiều 600 tâm A.
b) Ta có: ![]()
Khi đó điểm B biến thành điểm C qua phép quay ngược chiếu 3000 tâm A.
Bài toán 3. Cho hình vuông ABCD tâm O (hình vẽ). Nêu các phép quay giữ nguyên hình vuông đó.
Hướng dẫn giải
Hình vẽ minh họa:
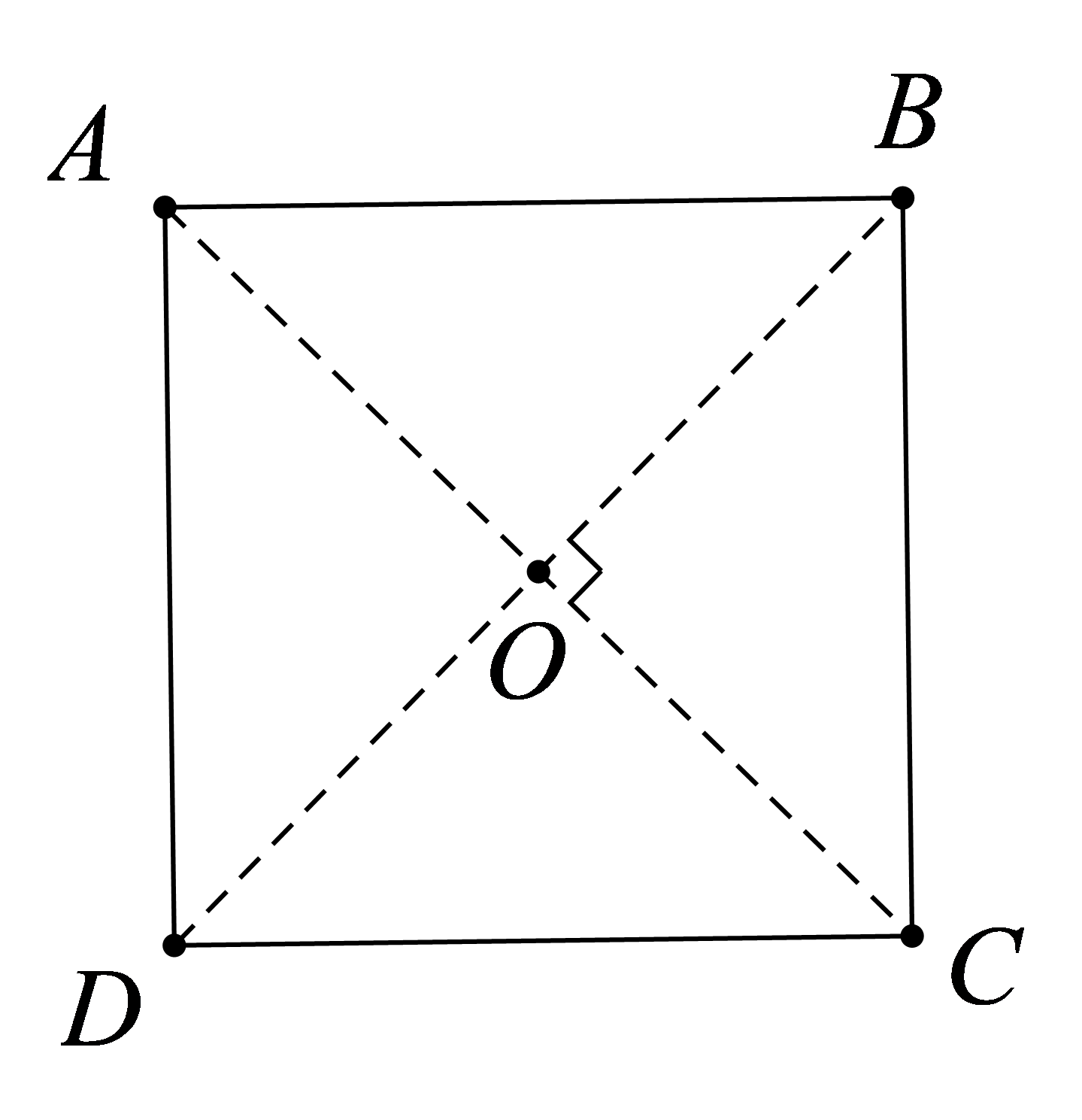
Ta có bốn điểm A; B; C; D thuộc đường tròn tâm O là giao điểm hai đường chéo AC và BD. Ta có ![]() .
.
Có 8 phép quay giữ nguyên hình vuông ABCD là:
Phép quay 900; 1800; 2700; 3600 tâm O thuận chiều.
Phép quay 900; 1800; 2700; 3600 tâm O ngược chiều.
Bài toán 4. Cho tam giác đều, thực hiện phép quay ngược chiều tâm A góc 900 ta được tam giác đều. Hãy vẽ tam giác đều đó.
Hướng dẫn giải
Hình vẽ minh họa:

Cách dựng: Phép quay ngược chiều 900 tâm A, biến điểm B biến thành điểm B'.
Xác định điểm B' theo hướng dẫn sau:
Vẽ đường tròn (A; AB) và tia Ax sao cho ![]() , tia Ax cắt đường tròn (A; AB) tại điểm B'.
, tia Ax cắt đường tròn (A; AB) tại điểm B'.
Tương tự ta dựng được điểm C'.
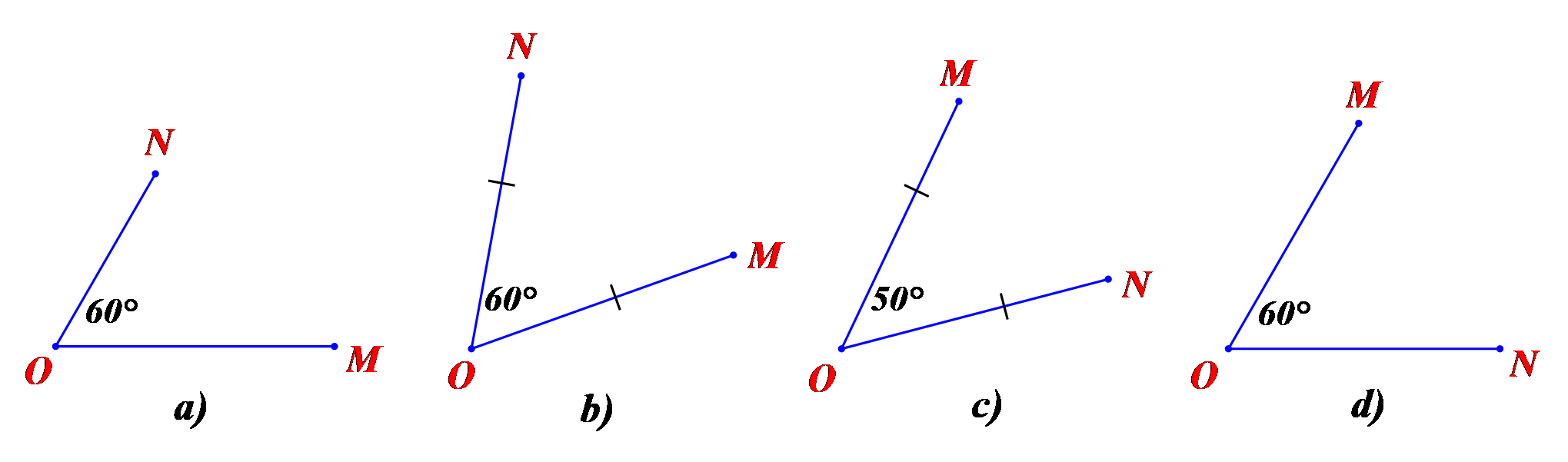
Bài toán 5. Trong các hình dưới đây, hình nào vē hai điểm M và N thoả mãn phép quay thuận chiếu 600 tâm O biến điểm M thành điểm N ?
Hướng dẫn giải
Phép quay thuận chiếu ![]() tâm O biến điểm M thành điểm N là hình d, vì ta có OM = ON và
tâm O biến điểm M thành điểm N là hình d, vì ta có OM = ON và ![]() .
.
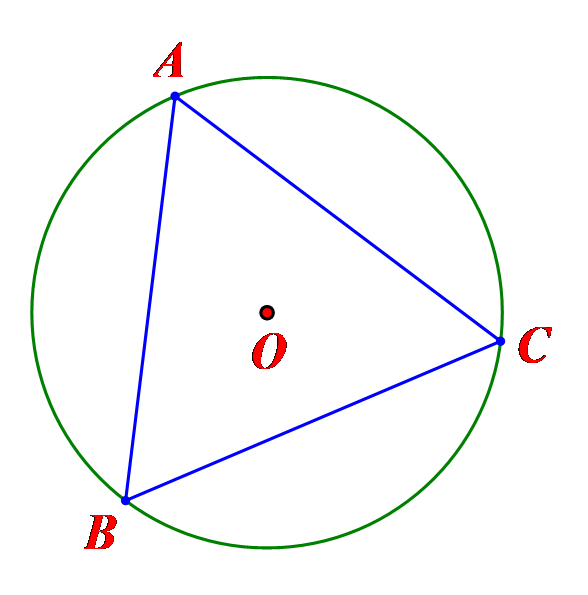
Bài toán 6. Cho tam giác đểu ABC nội tiếp dường tròn (O) như hình vẽ. Phép quay ngược chiếu 600 tâm O biến các điểm A; B; C lần lượt thành các điểm D; E; F. Chứng minh rằng ADBECF là một lục giác đều.
Hướng dẫn giải
Hình vẽ minh họa:
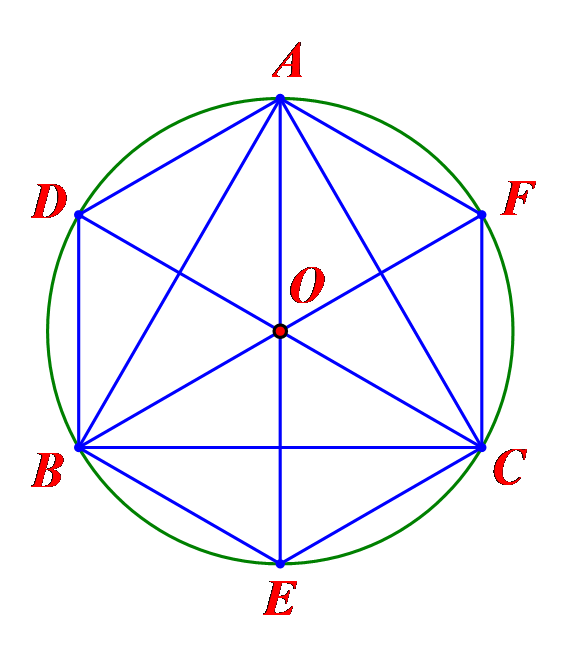
Phép quay ngược chiểu 600 tâm O biến A thành D.
Ta có: OD = OA và ![]() nên tam giác AOD là tam giác đều =>AD = OA = OD = R ( R là bán kính đường tròn (O)).
nên tam giác AOD là tam giác đều =>AD = OA = OD = R ( R là bán kính đường tròn (O)).
Chứng minh tương tự, ta có: BE = CF = R => AD = BE = CF = R (*)
Tam giác ABC đều nội tiếp đường tròn (O), ta có: OD = OA = OB (1)
Lại có ![]() mà
mà ![]() (cmt)
(cmt) ![]()
Từ (1) và (2) => Tam giác DOB là tam giác đều => Chứng minh tương tự các tam giác ECC và FOA cũng là tam giác đều => DB = EC = EA = R (**)
Từ (*) và ![]() (3)
(3)
Dễ thấy ![]() (4)
(4)
Từ (3) và (4) => ADBECF là một lục giác đều.
C. Bài tập tự rèn luyện có đáp án chi tiết
Bài 1. Cho tam giác đều ABC nội tiếp đường tròn (O). Hãy chỉ ra các phép quay biến tam giác thành chính nó.
Bài 2. Cho hình vuông nội tiếp đường tròn tâm O. hãy cho biết các phép quay thuận chiều lần lượt 900; 1800; 2700 với tâm O sẽ biến các điểm A; B; C; D thành những điểm nào?
Bài 3. Cho hình vuông ABCD có tâm O như hình vẽ. Phép quay thuận chiều tâm O biến điểm A thành điểm D thì các điểm B; C; D tương ứng biến thành các điểm nào?
Bài 4. Cho hình ngũ giác đều ABCDE có tâm O (Hình vẽ).
a) Phép quay ngược chiêu tâm O biến điểm A thành điểm B thì các điểm B, C, D, E tương ứng biến thành các điểm nào?
b) Chỉ ra ba phép quay tâm O giữ nguyên hình ngũ giác đều đã cho.
D. Đáp án bài tập tự rèn luyện
Bài 1
Hướng dẫn: Tương tự câu b, bài toán 1, có tất cả 6 phép quay đó là phép quay 1200; 2400; 3600 tâm ![]() thuận chiều và ngược chiều.
thuận chiều và ngược chiều.
Bài 2
Hình vẽ minh họa

Các phép quay thuận chiều lần lượt là 900; 1800; 2700 với tâm O biến các điểm A, B, C, D thành những điểm tương ứng cho bởi bảng sau:
|
Đỉnh Phép quay cùng chiều |
A |
B |
C |
D |
|
900 |
B |
C |
D |
A |
|
1800 |
C |
D |
A |
B |
|
2700 |
D |
A |
B |
C |
Bài 3
Ta có ABCD là hình vuông nên OA = OB = OC = OD và ![]() .
.
Ta có: ![]() .
.
Phép quay thuận chiều tâm O biến điểm A thành điểm D là phép quay 3.900 = 2700. Khi đó điểm B biến thành điểm A, điểm C biến thành điểm B và điểm D biến thành điểm B.
Bài 4
Hình vẽ minh họa

a) Phép quay ngược chiều 720 tâm O biến điểm A, biến B thì các điểm B, C, D, E lần lượt biến thành các điểm C, E, D và A.
b) Ba phép quay tâm O giữ nguyên hình ngũ giác đều:
1. Phép quay ngược chiểu 1440;
2. Phép quay ngược chiểu 2160;
3. Phép quay thuận chiểu 720.
Bạn hãy tìm thêm những phép quay còn lại giữ nguyên hình ngũ giác đều.
Bài 5.
Đa giác đều 12 cạnh ABCDEFGHIKLM nội tiếp đường tròn (O) (Xem hình vē).
Ta co: ![]()
và ![]()
Và OA = OB = OC = OD = ... (bán kính đường tròn ngoại tiếp)
Ta chọn phép quay thuận chiểu (hoặc ngược chiểu) góc quay 300; 600; 900; 1200 biến đa giác đã cho thành chính nó.
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
---------------------------------------------------
Vừa rồi là toàn bộ nội dung chuyên đề Phép quay Toán 9, bao gồm lý thuyết cần nhớ và các dạng bài tập ứng dụng thường gặp. Hy vọng tài liệu này sẽ giúp bạn hiểu sâu hơn về phép quay, rèn luyện kỹ năng giải bài tập và làm chủ nội dung hình học lớp 9. Đừng quên kết hợp với các chuyên đề khác như phép tịnh tiến, phép đối xứng để hệ thống hóa kiến thức toàn diện. Chúc bạn học tập tốt và đạt kết quả cao trong các kỳ thi!








