Cách xác định vị trí tương đối của hai đường tròn trong Toán 9 có đáp án
Bài tập vị trí tương đối hai đường tròn có đáp án
Trong chương trình Toán 9, chuyên đề Đường tròn là một phần kiến thức trọng tâm, giúp học sinh củng cố tư duy hình học và khả năng suy luận logic. Một trong những nội dung thường gặp là xác định vị trí tương đối của hai đường tròn – kiến thức quan trọng để giải quyết nhiều bài tập nâng cao.
Bài viết dưới đây sẽ hướng dẫn bạn cách xác định vị trí tương đối của hai đường tròn trong Toán 9 chi tiết, dễ hiểu, kèm hình minh họa và đáp án chuẩn SGK. Cùng khám phá để nắm chắc chuyên đề Đường tròn Toán 9 nhé!
A. Bảng tóm tắt vị trí tương đối của hai đường tròn phân biệt
Cho hai đường tròn phân biệt 
\((O;R)\) và \((O';R')\) với \(R \geq R'\). Ta có bảng sau:
|
Vị trí tương đối |
Số điểm chung |
Hệ thức liên hệ |
Hình ảnh minh họa |
|
Cắt nhau |
2 | \(R - R'
< OO' < R + R'\) |
 |
|
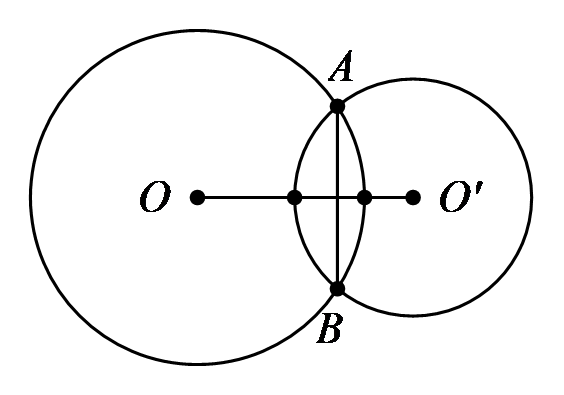Tiếp xúc ngoài |
1 | \(OO' = R
+ R'\) |
 |
|
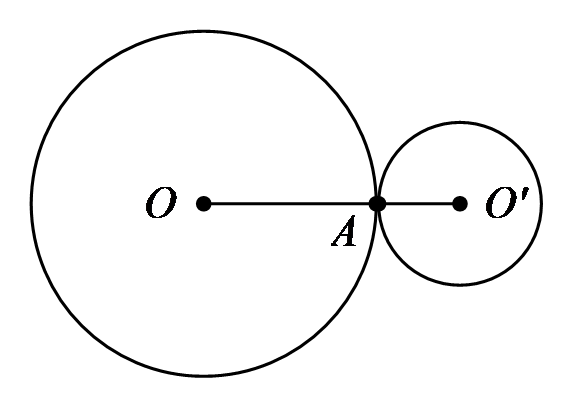Tiếp xúc trong |
1 | \(OO' = R
- R'\) |
 |
|
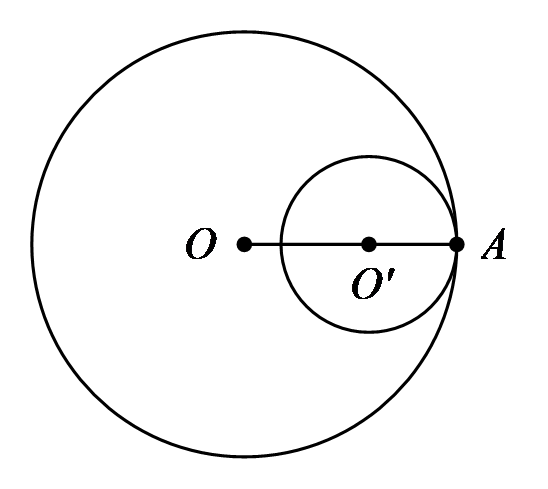Ngoài nhau |
0 | \(OO'
> R + R'\) |
 |
|
Đường tròn |
0 | \(OO'
< R - R'\) |
 |
B. Ví dụ minh họa xác định vị trí tương đối của hai đường tròn
Ví dụ 1. Cho hai điểm \(O\) và \(O'\) cách nhau một khoảng 5 cm. Mỗi đường tròn sau đây có vị trí tương đối như thế nào đối với đường tròn \((O;\ \ 3cm)\).
a) Đường tròn \((O';\ \ 3cm)\) b) Đường tròn \((O';\ \ 1cm)\) c) Đường tròn \((O';\ \ \ 8cm)\)
Hướng dẫn giải
a) Đặt \(R = 3cm,\ R' = 3cm\). Ta có:
\(3 - 3 < 5 < 3 + 3\)
\(R - R' < OO' < R +
R'\) hay \(0 < 5 <
6\)
Do đó hai đường tròn \((O;\ \
3cm)\) và\((O';\ \ 3cm)\) cắt nhau.
b) Đặt \(R = 3cm,\ R' = 1cm\). Ta có:
\(5 > 3 + 1\)
\(OO' > R + R'\)
Do đó hai đường tròn \((O;\ \
3cm)\) và \((O';\ \ 1cm)\) ở ngoài nhau.
c) Đặt \(R = 3cm,\ R' =
8cm\)
Ta có: \(5 = 8 - 3\) hay \(OO' = R' - R\)
Do đó hai đường tròn \((O;\ \
3cm)\)và \((O';\ \ \ 8cm)\) tiếp xúc nhau.
Ví dụ 2. Xác định vị trí tương đối của hai đường tròn \((O;\ \ R)\) và \((O';\ \ R')\)trong mỗi trường hợp sau:
a) \(OO' = 12;\ R = 5;\ R' =
3\); b) \(OO' = 8;\ R = 5;\ R'
= 3\);
c) \(OO' = 7;\ R = 5;\ R' =
3\); d) \(OO' = 0;\ R = 5;\ R'
= 4;\).
e) \(OO' = 3;\ R = 4;\ R' =
7.\)
Hướng dẫn giải
a) Ta có: \(12 > 5 + 3\) hay \(OO' > RR'.\)
Do đó hai đường tròn \((O;\ \
R)\) và\((O';\ \ R')\) ở ngoài nhau.
b) Ta có: \(8 = 5 + 3\) hay \(OO' = RR'.\)
Do đó hai đường tròn \((O;\ \
R)\) và\((O';\ \ R')\) tiếp xúc ngoài.
c) Ta có: \(5 - 3 < 7 < 5 +
3\) hay \(R - R' < OO' <
R + R'.\)
Do đó hai đường tròn \((O;\ \
R)\) và\((O';\ \ R')\) cắt nhau.
d) Ta có: \(0 < 5 - 4\) hay \(OO' < R - R'.\)
Do đó hai đường tròn \((O;\ \
R)\) đựng đường tròn\((O';\ \
R')\).
e) Ta có: \(3 = 7 - 4\) hay \(OO' = R' - R.\)
Do đó hai đường tròn \((O;\ \
R)\) và \((O';\ \ R')\) tiếp xúc trong.
Ví dụ 3. Cho hai điểm \(O\) và \(O'\) sao cho \(OO' = 3cm\). Mỗi đường tròn sau đây có vị trí tương đối như thế nào đối với đường tròn \((O;\ \ 3cm)\).
Hướng dẫn giải
Đặt \(R = 8cm,\ R' = 5cm\)
Ta có: \(3cm = 8cm - 5cm\)hay \(OO' = R - R'\)
Vậy hai đường tròn đã cho tiếp xúc trong với nhau.
Ví dụ 4. Cho đoạn thẳng \(OO'\) và điểm \(A\) nằm giữa hai điểm \(O\) và \(O'\). Vẽ đường tròn \((O;\ OA)\) và đường tròn \((O';\ O'A)\). Qua \(A\) vẽ đường thẳng cắt \((O)\) tại \(B\) và \((O')\) cắt tại \(C.\)
a) Chứng minh \((O)\) và \((O')\) tiếp xúc nhau.
b) Vẽ đường kính \(BD\) của \((O)\) và \(CE\) của \((O')\), chứng minh \(D,\ A,\ E\) thẳng hàng.
Hướng dẫn giải
Hình vẽ minh họa:
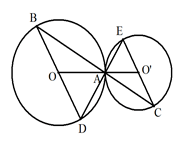
a) Ta có : \(OO' = OA + O'A\ (d = R
+ R')\)
Chứng tỏ \((O)\) và \((O')\)tiếp xúc ngoài tại \(A\).
b) Ta có \(BD\) là đường kính của \((O)\) nên \(OA = \frac{1}{2}BD\ \ \ \ \ \ \ \ \
(1)\)
Xét \(\Delta ABD\) có \(AO\) là trung tuyến (1) nên \(\Delta ABD\) vuông tại \(A\) hay \(AD\bot
AB,\) mà \(B,\ A,\ C\) thẳng hàng nên \(AD\bot BC,\) tương tự \(AE\bot BC.\)
Vì vậy \(AD\) và \(AE\) phải trùng nhau hay ba điểm \(D,\ A,\ E\) thẳng hàng.
C. Bài tập vận dụng xác định vị trí tương đối của hai đường tròn
Bài toán 1. Xác định vị trí của hai đường tròn \((O;\ 3cm)\)và \((O';\ 2cm)\) biết \(OO' > 5cm.\)
Bài toán 2. Cho hai điểm \(O\) và \(O'\) sao cho \(OO' = 2cm\). Xác định vị trí tương đối của hai đường tròn \((O;\ \ 5cm)\) và \((O';\ \ r)\) biết rằng \(r\ < \ 3cm\).
Bài toán 3. Cho ba điểm thẳng hàng \(O\), \(A\) và \(O'\). Với mỗi trường hợp sau hãy viết hệ thức giữa các độ dài \(OO',\
OA\) và \(O'A\) rồi xét xem hai đường tròn \((O;\ OA)\) và \((O';\ O'A)\) tiếp xúc trong hay tiếp xúc ngoài với nhau; vẽ hình để khẳng định dự đoán của mình.
a) Điểm \(A\) nằm giữa hai điểm \(O\) và \(O'\);
b) Điểm \(O\) nằm giữa hai điểm \(A\) và \(O'\);
c) Điểm \(O'\) nằm giữa hai điểm \(A\) và \(O\).
Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!
------------------------------
Trên đây là toàn bộ kiến thức giúp bạn xác định vị trí tương đối của hai đường tròn trong Toán 9 – một phần quan trọng trong chuyên đề Đường tròn Toán 9.
Hy vọng bài viết giúp bạn hiểu rõ hơn về tính đối xứng của đường tròn, mối quan hệ giữa hai đường tròn cắt nhau, tiếp xúc hay không giao nhau, và vận dụng thành thạo trong giải bài tập hình học.
👉 Hãy lưu lại hoặc chia sẻ bài viết này để cùng bạn bè ôn tập hiệu quả Toán 9, chuẩn bị tốt cho kỳ thi học kỳ và vào lớp 10 nhé!
