Tỉ số lượng giác của góc nhọn

Tỉ số lượng giác của góc nhọn là một trong những chuyên đề trọng tâm trong chương trình Toán lớp 9, đóng vai trò nền tảng để học sinh hiểu sâu hơn về hàm số lượng giác và ứng dụng trong tam giác vuông. Kiến thức này không chỉ xuất hiện nhiều trong các bài kiểm tra và đề thi học kỳ, mà còn là bước đệm quan trọng giúp các em chinh phục phần hình học không gian và lượng giác lớp 10 – 11.

Trong bài viết này, chúng ta sẽ cùng tìm hiểu khái niệm, công thức, cách ghi nhớ nhanh và ví dụ minh họa chi tiết về tỉ số lượng giác của góc nhọn, giúp học sinh nắm chắc lý thuyết, vận dụng thành thạo vào bài tập, đồng thời rút ra mẹo học hiệu quả để đạt điểm cao trong các kỳ thi.

1. Công thức tỉ số lượng giác của góc nhọn

Hình vẽ minh họa

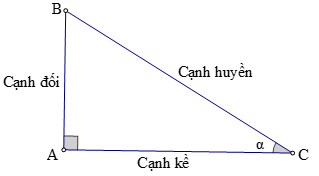
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sinα.

+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu là cosα.

+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu là tanα.

+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu là cotα.

Hay sinα = AB/BC; cosα = AC/BC; tanα = AB/AC; cotα = AC/AB.

Nhận xét: Nếu α là một góc nhọn thì 0 < sinα < 1; 0 < cosα < 1; tanα > 0; cotα > 0.

2. Tỉ số lượng giác của hai góc phụ nhau

Với hai góc α, β mà α + β = 90° ta có:

sinα = cosβ;                       cosα = sinβ;

tanα = cotβ;                      cotα = tanβ.

Nếu hai góc nhọn α và β có sinα = sinβ hoặc cosα = cosβ thì α = β.

3. Một số góc đặc biệt

Với một số góc đặc biệt ta có:

\(\sin {30^0} = \cos {60^0} = \frac{1}{2};\)                  \(\sin {45^0} = \cos {45^0} = \frac{{\sqrt 2 }}{2}\)

\(\cos {30^0} = \sin {60^0} = \frac{{\sqrt 3 }}{2};\)               \(\cot {60^0} = \tan {30^0} = \frac{1}{{\sqrt 3 }}\)

\(\tan {45^0} = \cot {45^0} = 1;\)                     \(\cot {30^0} = \tan {60^0} = \sqrt 3\)

4. Bài tập tỉ số lượng giác của góc nhọn có đáp án 

Hướng dẫn giải

Hình vẽ minh họa:

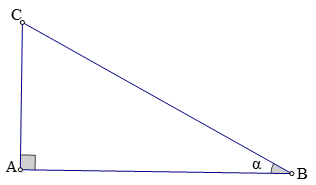
Cách 1. Xét tam giác ABC vuông tại A.

Đặt \(\widehat{B} = \alpha\) . Ta có: \(\sin\alpha = \frac{AC}{BC} = \frac{5}{13}\)

=> \(\frac{AC}{5} = \frac{BC}{13} = k\)

\(=> AC = k, BC = 13k\).

Tam giác ABC vuông tại A nên:

\(AB^{2} = BC^{2} - AC^{2} = (13k)^{2} - (5k)^{2} = 144k^{2}\)

\(=> AB = 12k\)

Vậy \(\cos\alpha = \frac{AB}{BC} = \frac{12k}{13k} = \frac{12}{13}\) ; \(\tan\alpha = \frac{AC}{AB} = \frac{5k}{12k} = \frac{5}{12};\)\(\cot\alpha = \frac{AB}{AC} = \frac{12k}{5k} = \frac{12}{5}\)

Cách 2. Ta có:

\(\sin\alpha = \frac{5}{13}\) => \(\sin^{2}\alpha = \frac{25}{169}\)

Mà \(sin^{2}\alpha + cos^{2}\alpha = 1\)

=> \(cos^{2}\alpha = 1 - sin^{2}\alpha = 1 - \frac{25}{169} = \frac{144}{169}\)

=> \(\cos\alpha = \frac{12}{13}\)

=> \(\tan\alpha = \frac{\sin\alpha}{\cos\alpha} = \frac{5}{13}:\frac{12}{13} = \frac{5}{13}.\frac{13}{12} = \frac{5}{12}\)

=> \(\cot\alpha = \frac{\cos\alpha}{\sin\alpha} = \frac{12}{13}:\frac{5}{13} = \frac{12}{13}.\frac{13}{5} = \frac{12}{5}\) .

Ở cách giải thứ nhất ta biểu thị độ dài các cạnh của tam giác ABC theo đại lượng k rồi sử dụng định nghĩa tỉ số lượng giác của góc nhọn để tính \(\cos\alpha,tan\alpha,cot\alpha\) . Ở cách giải thứ hai, ta sử dụng giả thiết \(\sin\alpha = \frac{5}{13}\) để tính \(sin^{2}\alpha\) rồi tính \(\cos\alpha\) từ \(sin^{2}\alpha + cos^{2}\alpha = 1\) . Sau đó ta tính \(\tan\alpha\) và \(\cot\alpha\) qua \(\sin\alpha\) và \(\cos\alpha\) .

Hướng dẫn giải

Biết \(\sin\alpha.cos\alpha = \frac{12}{25}\).

Để tính \(\sin\alpha,cos\alpha\) ta cần tính \(\sin\alpha + \cos\alpha\) rồi giải phương trình với ẩn là \(\sin\alpha\) hoặc \(\cos\alpha\).

Ta có:

\(\left( \sin\alpha + \cos\alpha\right)^{2}\)\(= sin^{2}\alpha + \cos^{2}\alpha + 2\sin\alpha.cos\alpha\)

\(= 1 + 2.\frac{12}{25} = \frac{49}{25}\)

=> \(\sin\alpha + \cos\alpha = \frac{7}{5}\) nên \(\sin\alpha = \frac{7}{5} - \cos\alpha\)

=> \(\cos\alpha\left( \frac{7}{5} -\cos\alpha \right) = \frac{12}{25}\)

\(\Leftrightarrow \frac{7}{5}\cos\alpha- cos^{2}\alpha = \frac{12}{25}\)

\(\begin{matrix} \Leftrightarrow 25{\cos ^2}\alpha - 35\cos \alpha + 12 = 0 \hfill \\ \Leftrightarrow 5\cos \alpha \left( {5\cos \alpha - 4} \right) - 3\left( {5\cos \alpha - 4} \right) = 0 \hfill \\ \Leftrightarrow \left( {5\cos \alpha - 4} \right)\left( {5\cos \alpha - 3} \right) = 0 \hfill \\ \end{matrix}\)

=> \(\cos\alpha = \frac{4}{5}\) hoặc \(\cos\alpha = \frac{3}{5}\)

+ Nếu \(\cos\alpha = \frac{4}{5}\) thì \(\sin\alpha = \frac{12}{25}:\frac{4}{5} = \frac{3}{5}\).

+ Nếu \(\cos\alpha = \frac{3}{5}\) thì \(\sin\alpha = \frac{12}{25}:\frac{3}{5} = \frac{4}{5}\).

Vậy \(\sin\alpha = \frac{3}{5}\), \(\cos\alpha = \frac{4}{5}\) hoặc \(\sin\alpha = \frac{4}{5},cos\alpha = \frac{3}{5}\).

Hướng dẫn giải

Hình vẽ minh họa:

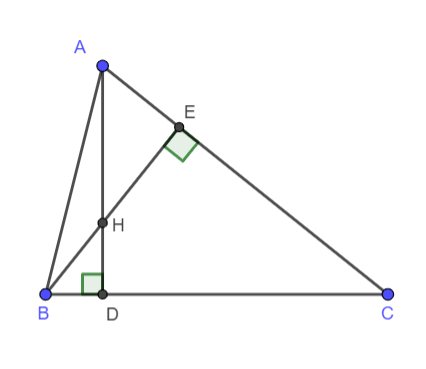
Ta có: \(\tan B = \frac{AD}{BD};tanC = \frac{AD}{CD}\).

=> \(\tan B.tanC = \frac{AD^{2}}{BD.CD}\) (1)

\(\widehat{HBD} = \widehat{CAD}\) (cùng phụ với \(\widehat{ACB}\))

\(\widehat{HDB} = \widehat{ADC} = 90^{0}\)

=> \(\Delta BDH\sim\Delta ADC\) (g - g)

=> \(\frac{DH}{DC} = \frac{BD}{AD}\)

=> BD . DC = DH . AD (2).

Từ (1) và (2)

=> \(\tan B.\tan C = \frac{AD^{2}}{DH.AD}= \frac{AD}{DH}\) (3).

Theo giả thiết ta có:

\(\frac{HD}{AH} = \frac{1}{2}\) suy ra \(\frac{HD}{AH + HD} = \frac{1}{2 + 1}\) hay \(\frac{HD}{AD} = \frac{1}{3}\)

=> AD = 2HD

Thay vào (3) ta được: \(\tan B.\tan C = \frac{3HD}{DH} = 3\).

Hướng dẫn giải:

Hình vẽ minh họa

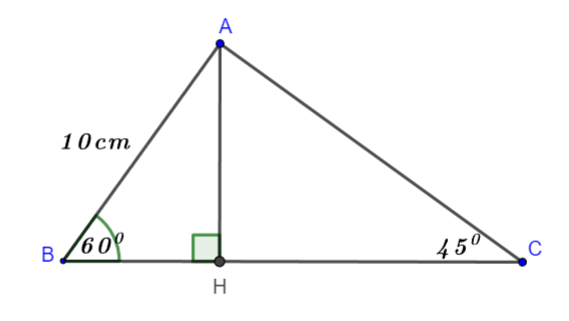
Kẻ đường cao AH.

Xét tam giác ABH vuông tại H ta có:

\(\sin B = \frac{AH}{AB} \Leftrightarrow \sin60^{0} = \frac{AH}{10}\)

\(\Rightarrow AH = 10.\sin60^{0} =5\sqrt{3}(cm)\)

\(\cos B = \frac{BH}{AB} \Leftrightarrow \cos60^{0} = \frac{BH}{10}\)

\(\Rightarrow BH = 10.\cos60^{0} =5(cm)\)

Xét tam giác ACH vuông tại H và \(\widehat{C} = 45^{0}\) nên tam giác AHC vuông cân tại H

Suy ra \(AH = HC = 5\sqrt{3}(cm)\)

\(AC = AH\sqrt{2} = 5\sqrt{3}.\sqrt{2} = 5\sqrt{6}(cm)\)

\(\Rightarrow BC = BH + HC = 5 + 5\sqrt{3}(cm)\)

Vậy chu vi tam giác ABC bằng \(AB + AC + BC \approx 36(cm)\).

Hướng dẫn giải

Hình vẽ minh họa

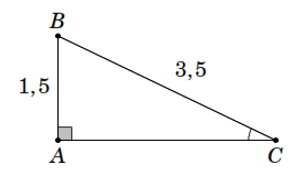
Áp dụng định lý Pythagore cho tam giác ABC vuông tại A ta có:

\(AB^2+AC^2=BC^2\)

Suy ra:

\(AC^{2} = BC^{2} - AB^{2} = 3,5^{2}- 1,5^{2} = 10\)

\(\Rightarrow AC = \sqrt{10}\). 

Do đó \(\cos B = \sin C = \frac{AB}{BC} = \frac{1,5}{3,5} \approx 0,4286\)

\(\sin B = \cos C = \frac{AC}{BC} = \frac{\sqrt{10}}{3,5} \approx 0,9035\)

\(\cot B = \tan C = \frac{AB}{AC} = \frac{1,5}{\sqrt{10}} \approx 0,4743\)

\(\tan B = \cot C = \frac{AC}{AB} = \frac{\sqrt{10}}{1,5} \approx 2,1082\)

Hướng dẫn giải

Hình vẽ minh họa:

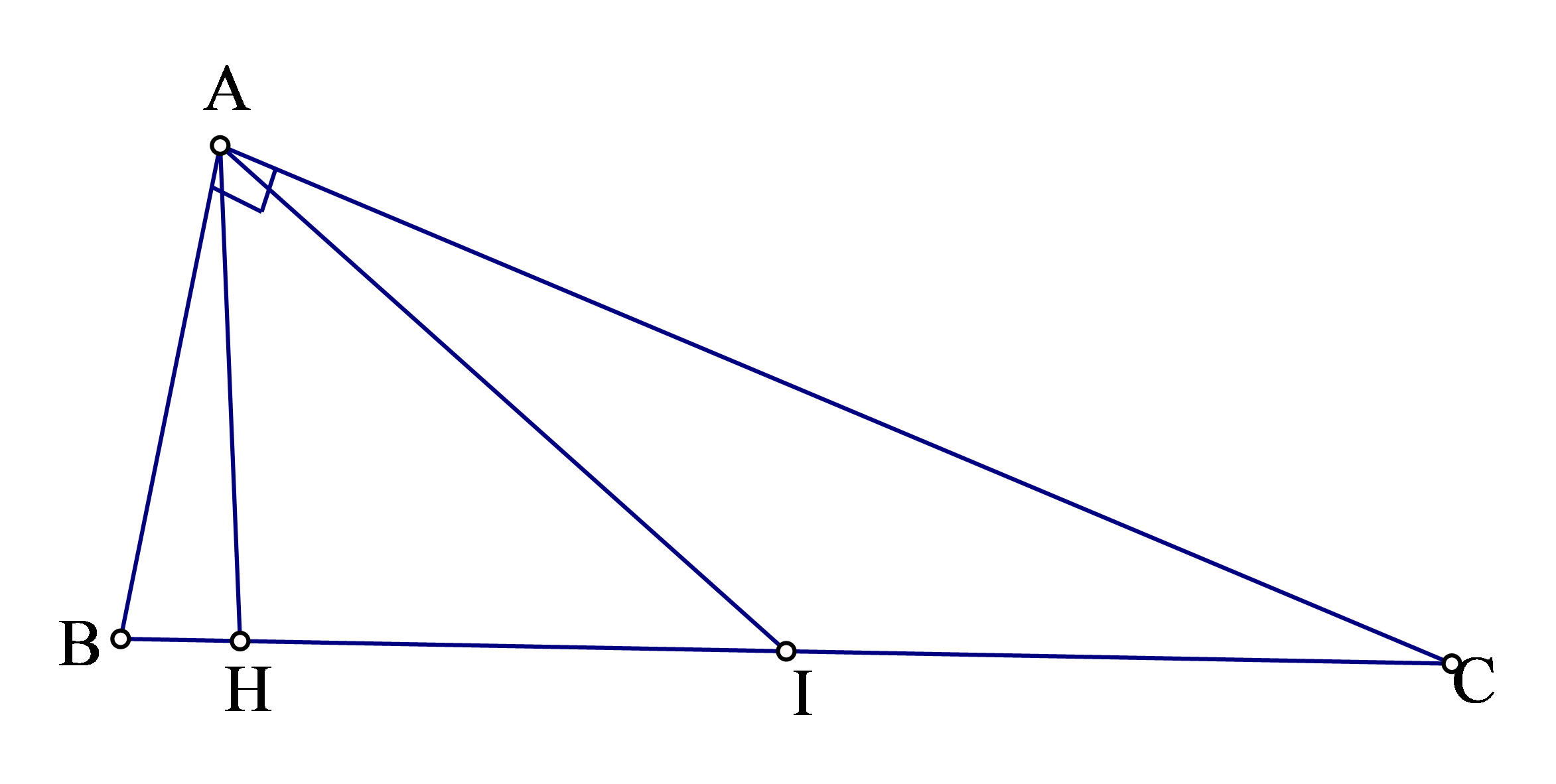
Vẽ tam giác \(ABC\) vuông tại \(A\), với \(BC = 2a\) (\(a\) là một độ dài tùy ý), \(\widehat{C} = 15^{0}\), suy ra \(\widehat{B} = 75^{0}\).

Gọi \(I\) là trung điểm của \(BC\), ta có:

\(IA = IB = IC = a\).

Vì \(\widehat{AIB}\) là góc ngoài tại đỉnh \(I\) của tam giác cân \(IAC\) nên \(\widehat{AIB} = 2\widehat{C} = 30^{0}\).

Kẻ \(AH\bot BC\) thì \(IH = AI.\cos30^{0} = \frac{a\sqrt{3}}{2}\); \(AH = AI.\cos30^{0} = \frac{a}{2}\);

\(CH = CI + IH = a + \frac{a\sqrt{3}}{2} = \frac{a\left( 2 + \sqrt{3} \right)}{2}\).

Tam giác \(AHC\) vuông tại \(H\), theo định lý Pythagore, ta có:

\(AC^{2} = CH^{2} + AH^{2} = \frac{a^{2}\left( 2 + \sqrt{3} \right)^{2}}{4} + \frac{a^{2}}{4}\)

\(= \frac{a^{2}\left( 4 + 4\sqrt{3} + 3 + 1 \right)}{4}\) \(= \frac{4a^{2}\left( 2 + \sqrt{3} \right)}{4} = a^{2}\left( 2 + \sqrt{3} \right)\)

suy ra \(AC = a\sqrt{2 + \sqrt{3}}\)

\(\sin75^{0} = \sin B\)\(= \frac{AC}{BC}\)

\(= \frac{a\sqrt{2 +\sqrt{3}}}{2a} = \frac{\sqrt{2 + \sqrt{3}}}{2}\)\(= \frac{\sqrt{4 +2\sqrt{3}}}{2\sqrt{2}}\)

\(=\frac{\sqrt{\left( \sqrt{3} + 1 \right)^{2}}}{2\sqrt{2}} =\frac{\sqrt{3} + 1}{2\sqrt{2}}\)

\(= \frac{\sqrt{2}\left( \sqrt{3} + 1\right)}{2\sqrt{2}.\sqrt{2}} = \frac{\sqrt{6} +\sqrt{2}}{4}\).

Vậy \(\sin75^{0} = \frac{\sqrt{6} +\sqrt{2}}{4}\).

--------------------------------------------------------------

Qua nội dung bài viết trên, chắc hẳn các em đã hiểu rõ tỉ số lượng giác của góc nhọn là gì, cách xác định sin, cos, tan, cot của một góc trong tam giác vuông và mối liên hệ giữa các tỉ số lượng giác. Việc nắm vững kiến thức này không chỉ giúp học tốt môn Toán lớp 9, mà còn tạo nền tảng vững chắc cho các chuyên đề lượng giác lớp 10 và hình học không gian sau này. Hãy thường xuyên ôn tập công thức, làm bài tập vận dụng, và tham khảo thêm các chuyên đề môn Toán lớp 9 có đáp án chi tiết để củng cố kiến thức toàn diện.